概述
| Time Limit: 12000MS | Memory Limit: 65536K | |
| Total Submissions: 1921 | Accepted: 779 | |
| Case Time Limit: 2000MS | ||
Description
A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules that describe the new state of a cell based on the states of neighboring cells. The order of the cellular automaton is the number of cells it contains. Cells of the automaton of order n are numbered from 1 to n.
The order of the cell is the number of different values it may contain. Usually, values of a cell of order m are considered to be integer numbers from 0 to m − 1.
One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. In this problem we examine the special kind of cellular automaton — circular cellular automaton of order n with cells of order m. We will denote such kind of cellular automaton as n,m-automaton.
A distance between cells i and j in n,m-automaton is defined as min(|i − j|, n − |i − j|). A d-environment of a cell is the set of cells at a distance not greater than d.
On each d-step values of all cells are simultaneously replaced by new values. The new value of cell i after d-step is computed as a sum of values of cells belonging to the d-enviroment of the cell i modulo m.
The following picture shows 1-step of the 5,3-automaton.
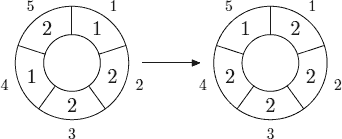
The problem is to calculate the state of the n,m-automaton after k d-steps.
Input
The first line of the input file contains four integer numbers n, m, d, and k (1 ≤ n ≤ 500, 1 ≤ m ≤ 1 000 000, 0 ≤ d < n⁄2 , 1 ≤ k ≤ 10 000 000). The second line contains n integer numbers from 0 to m − 1 — initial values of the automaton’s cells.
Output
Output the values of the n,m-automaton’s cells after k d-steps.
Sample Input
sample input #1 5 3 1 1 1 2 2 1 2 sample input #2 5 3 1 10 1 2 2 1 2
Sample Output
sample output #1 2 2 2 2 1 sample output #2 2 0 0 2 2
Source
分析：线性代数没学好，表示很有鸭梨~~~~
转：糯米。。。。
======================================================================================
这题对我来说太难啦，看了报告半天才弄明白是咋回事。
高手们的解题报告相当飘逸。我来写一个造福菜鸟的。
首先来看一下Sample里的第一组数据。
1 2 2 1 2
经过一次变换之后就成了
5 5 5 5 4
它的原理就是
a0 a1 a2 a3 a4
->
(a4+a0+a1) (a0+a1+a2) (a1+a2+a3) (a2+a3+a4) (a3+a4+a0)
如果用矩阵相乘来描述，那就可以表述为1xN和NxN的矩阵相乘，结果仍为1xN矩阵
a = 1 2 2 1 2
b =
1 1 0 0 1
1 1 1 0 0
0 1 1 1 0
0 0 1 1 1
1 0 0 1 1
a * b = 5 5 5 5 4
所以最终结果就是：a * (b^k)
线性代数不合格的同鞋表示压力很大。。
对一个NxN矩阵求k次方，而且这个k很大，N也不小，怎么办？
所以有高手观察到了，这个矩阵长得有点特殊，可以找到一些规律：
b^1 =
[1, 1, 0, 0, 1]
[1, 1, 1, 0, 0]
[0, 1, 1, 1, 0]
[0, 0, 1, 1, 1]
[1, 0, 0, 1, 1]
b^2 =
[3, 2, 1, 1, 2]
[2, 3, 2, 1, 1]
[1, 2, 3, 2, 1]
[1, 1, 2, 3, 2]
[2, 1, 1, 2, 3]
b^3 =
[7, 6, 4, 4, 6]
[6, 7, 6, 4, 4]
[4, 6, 7, 6, 4]
[4, 4, 6, 7, 6]
[6, 4, 4, 6, 7]
b^4 =
[19, 17, 14, 14, 17]
[17, 19, 17, 14, 14]
[14, 17, 19, 17, 14]
[14, 14, 17, 19, 17]
[17, 14, 14, 17, 19]
发现神马没有。就是无论是b的几次幂，都符合A[i][j] = A[i-1][j-1]
高手说是这样推倒出来地：
######
利用矩阵A，B具有a[i][j]=A[i-1][j-1],B[i][j]=B[i-1][j-1]（i-1<0则表示i-1+n,j-1<0则表示j-1+n）
我们可以得出矩阵C=a*b也具有这个性质
C[i][j]=sum(A[i][t]*B[t][j])=sum(A[i-1][t-1],B[t-1][j-1])=sum(A[i-1][t],B[t][j-1])=C[i-1][j-1]
######
这样就可以开一个N大小的数组来存放每次计算的结果了。而没必要用NxN。
N的问题解决了，但是k还是很大，怎么办？
这时候可以用二分法来求b^k
b^k = b^1 * b^4 * b^16 。。。
计算过程中，必定会出现数字大于M的情况。
切记 x*y = (x%M)*(y%M)
最后，经过多次优化，这题的代码居然被高手写成了如下的一小坨，实在是。。给力哇
=================================================================================
看到循环卷积，我果断不会，摆渡一下，竟然有o（n)算法，果断学了，写出代码，才发现鸭梨更大，中间部分不能取模，这算法没法用了
贴下代码：哎~~~
最后
以上就是花痴小白菜为你收集整理的poj 3150的全部内容，希望文章能够帮你解决poj 3150所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复