Cellular Automaton (矩阵乘法)

Problem Description

A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules that describe the new state of a cell based on the states of neighboring cells. The order of the cellular automaton is the number of cells it contains. Cells of the automaton of ordern are numbered from 1 to n.

The order of the cell is the number of different values it may contain. Usually, values of a cell of order m are considered to be integer numbers from 0 to m − 1.

One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. In this problem we examine the special kind of cellular automaton — circular cellular automaton of order n with cells of order m. We will denote such kind of cellular automaton as n,m-automaton.

A distance between cells i and j in n,m-automaton is defined as min(|i − j|, n − |i − j|). A d-environment of a cell is the set of cells at a distance not greater than d.

On each d-step values of all cells are simultaneously replaced by new values. The new value of cell i after d-step is computed as a sum of values of cells belonging to the d-enviroment of the cell i modulo m.

The following picture shows 1-step of the 5,3-automaton.

 

Input

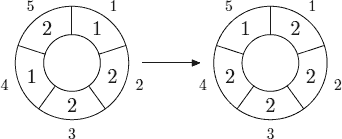
The first line of the input file contains four integer numbers n, m, d, and k (1 ≤ n ≤ 500, 1 ≤ m ≤ 1 000 000, 0 ≤ d < ⁿ⁄₂ , 1 ≤ k ≤ 10 000 000). The second line contains n integer numbers from 0 to m − 1 — initial values of the automaton’s cells.

 

Output

Output the values of the n,m-automaton’s cells after k d-steps.

 

Sample Input

sample input #1 5 3 1 1 1 2 2 1 2 sample input #2 5 3 1 10 1 2 2 1 2

 

Sample Output

sample output #1 2 2 2 2 1 sample output #2 2 0 0 2 2

 **************************************************************************************************************************

/*
矩阵乘法
原理：
它的原理就是
a0 a1 a2 a3 a4
->
(a4+a0+a1) (a0+a1+a2) (a1+a2+a3) (a2+a3+a4) (a3+a4+a0)
*/
#include<iostream>
#include<cstdio>
using namespace std;
int n,m,d,k;
void mul(long long a[],long long b[])
{

int i,j;

long long c[501];

for(i=0;i<n;++i)for(c[i]=j=0;j<n;++j)c[i]+=a[j]*b[i>=j?(i-j):(n+i-j)];

for(i=0;i<n;b[i]=c[i++]%m);
}
long long init[501],tmp[501];
int main()
{

int i,j;

scanf("%d%d%d%d",&n,&m,&d,&k);

for(i=0;i<n;++i)scanf("%I64d",&init[i]);

for(tmp[0]=i=1;i<=d;++i)tmp[i]=tmp[n-i]=1;//n*n的矩阵初始化

while(k)//二分求解

{

if(k&1)mul(tmp,init);

mul(tmp,tmp);

k>>=1;

}

for(i=0;i<n;++i)if(i)printf(" %I64d",init[i]);else printf("%I64d",init[i]);

printf("n");

return 0;
}