图像处理 - 傅里叶变换的思想

傅里叶变换的核心：试图寻找一组正交基来表示原函数（信号等物理模型），以实现从空域到频域的转换。

一．正交

在试图理解傅里叶变换之前，必须先理解正交。欲想理 解事物，我们首先要学会将其分解，将之分解成不同的元素，如果这些元素之间互不相关，我们就可以对其分而治之了，分而解之了。

（1）正交来源

线性代数的基。基是刻画向量空间的工具，是向量空间的一个子集。向量空间中的任意一个向量都可以用基来唯一表示。在这个基础上提出了正交基。正交基的优点一方面在于各个基之间互不干扰，另一方面如果采用正交基， 变换域系数会没有冗余信息， 变换前后的信号能量相等，等于是用最少的数据表达最大的信息量， 利于数值压缩等领域。 比如典型的正交基： 二维笛卡尔坐标系的（1,0） 、 （0,1） ， 用它们表达一个信号显然非常高效，计算简单。 而如果用三个互成120° 的向量表达， 则会有信息冗余， 有重复表达。根据奥卡姆剃刀原理， 自然应该选择前者。 如果从矩阵的角度来说， 就是满足要求下， 矩阵越稀疏越好。

（2）正交的定义

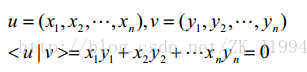
有了向量正交的例子之后，我们引入函数正交：

稍微回忆积分的定义，容易看出，上式可以过渡到积分形式。因此引出函数正交的定义，若有下式成立（或者在某区间上成立）：

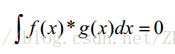
则称函数f(x)与g(x)正交。

（3）正交函数基

满足正交性的函数有许多，而傅里叶变换采用了一种最基础的正交基：

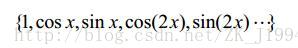
在这组基中，任意拿出其中两个不同的函数，他们会满足正交。

那么，我们就可以用这组正交函数基来表示任意函数（或者信号）:

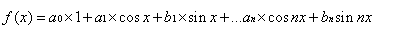
  如果你确实将一个函数表示成了傅里叶级数，那么对于分析这个函数就太简单了，以滤波为例，如果我们需要得到低频（频率<f）图像，那么就可以将分量cos(nx)=cos(2πfx)以后的全部丢掉就OK了。这样，我们就可以得到任何频率的图像了。

二．傅里叶变换

众所周知，在图像处理中，有两个极重要处理方式：空域和频域。空域优点：空域最大好处是直观，直接操作图像像素值。频域优势：频域在空域的基础上抽象了一层，采用“频率”来代表像素之间的变化和波动，这种方式更加全局。这有点类似PO和OO的思想。

那么我们可能会问到“如何转换到频域?”，对这就是傅里叶变换的作用。

三．频域处理的一般过程

最后谈谈，频域处理的一般过程，仍然以频域滤波为例，因为其他的方面不是太懂。

（1）将原图像进行傅里叶变换

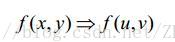
（2）寻找传递函数（核心）

（3）卷积定理

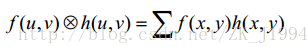
从这里也容易看出：滤波就是在空域上做卷积，或者频域上做乘积。

（4）反傅里叶变换

最后

以上就是谨慎煎饼为你收集整理的图像处理 - 傅里叶变换的思想的全部内容，希望文章能够帮你解决图像处理 - 傅里叶变换的思想所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。