矩阵压缩学习笔记

矩阵的压缩储存：
在一些高阶矩阵中，非零元素非常少，此时如果使用二维数组将造成 

储存空间的浪费，这时可只储存部分元素，从而提高储存空间的利用
率，通常的做法是为多个相同值的元素只分配一个储存单元，对值为
零的元素不分配储存单元。我们把非零元素个数远小于二维数组总元
素个数，或元素分布呈一定规律的（对称矩阵，三角矩阵，对角矩阵）
特殊矩阵压缩储存。

对称矩阵：
矩阵元素的值与下标的关系： a(i,j) = a(j,i) 

我们只需为每一对称元素分配一个储存单元，

这样可以将 n*n 个 元素储存在一个 n(n+1)/2 的储存空间里。

假设用以为数组储存上三角或下三角元素。

则一维数组的下标 k 与 n 阶对称阵的元素 a(i,j) 的下标对应关系为：

如果 i >= j 时，以下三角储存，

k = i*(i+1)/2 + j 如果 i < j 时，

以上三角储存， k = j*(j+1)/2 + i
例如：

   该矩阵对角线上的数字为 1 8 9 10，在对角线两边的元素是对称的，整个矩阵满足a[i][j] = a[j][i]
    当我们队该矩阵无压缩存储时，我们需要使用4*4 = 16个存储空间，但是由于它是对称的，

    因此我们可以只保存矩阵的上三角或者下三角，这样我们就可以得到整个矩阵模型，而使用的存储空间也会缩小到10.
    至此，假设我们拥有一个n*n的对称矩阵，那么我们只需要 n*(n+1)/2 个存储空间就可以将整个矩阵模型保存下来。
   假设我们以下三角元素进行存储，那么则有数组 arr[]

   其中：
   第一行： 1
   第二行： 2 8
   第三行： 3 5 9
   第四行： 4 6 7 10
   我们可以发现，当我们准备求得 a[i][j] 元素值时（当 i>=j ，即在下三角内），对应在 arr 数组内的下标为 i*(i+1)/2+j 。
   即当 i>=j 时，a[i][j] = arr[i*(i+1)/2+j]；当 i<j 时，a[i][j] = arr[j*(j+1)/2+i]。
  当我们在求 a[i][j] 时，由于我们保存的只是下三角元素，因此第 i 行以上的元素一共有 i*(i+1)/2 个，而 j 恰恰在最后一行的第 j 列，因此在数组中该数字的位置为 i*(i+1)/2+j）

   对称矩阵压缩完成。

三角矩阵：

 1.上三角矩阵：

分为上三角矩阵和下三角矩阵，其中在上三角矩阵中，下三角元素
全部为一个常数c,下三角矩阵中，上三角元素全部为一个常数c。
以上三角矩阵为例，上三角矩阵的压缩规则是只储存上三角元素，
不储存下三角元素，或只用一个储存单元储存下三角非零元素
用一维数组储存上三角矩阵，采取使用一个储存单元储存下三角元
素的方法，一维数组的长度为 n*(n+1)/2 + 1 一维数组的下标 k与
n 阶上三角矩阵的元素 a(i,j) 的下标对应关系为：
如果 i <= j, k = i*(2n-i+1)/2 + j -i
如果 i > j , k = n*(n+1)/2
下三角矩阵使用一维数组储存后相应的对应关系为：
如果 i >= j, k = i*(i+1)/2 + j
如果 i <
j, k = n*(n+1)/2 

/*
上三角矩阵：
下三角：
*/

  下三角矩阵的压缩方式同对称矩阵的压缩方式相同，矩阵内元素与数组元素的对应位置关系也是相同的。
   所以对于下三角矩阵来讲：
   当 i>=j 时，a[i][j] = arr[i*(i+1)/2+j]；当 i<j 时，a[i][j] = 0；

   当我们对上三角矩阵进行压缩时：
   当 i<=j 时， a[i][j] = arr[i*(2*n-i+1)+j-i]；当 i>j 时，a[i][j] = 0；

   当然，我们这里仅仅是把对角线的一边全部看做是零，当实际应用过程中，有可能对角线的一边不是零而是其他的一个值 C，那么我们就可以构造一个 n*(n+1)/2+1 的数组，最后一个位置保存 C 的值。

对角矩阵：

 除了主对角线元素不为零其余所有元素均为零的矩阵。

 如：

   此类型的矩阵，我们只需要构建一个长度为 n 的数组 arr[] 保存对角线元素即可。
   当 i==j 时，a[i][j] = arr[i]；当 i != j 时，arr[i][j] = 0；
   当然，我们这里的对角矩阵可以不符合定义，假设我们主对角线的上半部分值为 C，下半部分值为 D，

   那么我可以构建一个长度为 n+2 的数组arr[] 保存对角线元素，同时最后两位保存C和D。
   当i < j 时，a[i][j] = C；当 i == j 时，a[i][j] = arr[i]；当 i > j 时，arr[i][j] = D；

    

以三元组压缩:

矩阵压缩是将矩阵存储于一位数组，以节约空间。那么根据矩阵（i，j） == 矩阵（j，i）；我们就可以只存储“矩阵（i，j）”了。

当要访问矩阵（j,i）时交换 i 和 j 就可以了。
那么怎么压缩矩阵呢?，可以看出对于下面的例子中存储上三角和下三角都可以，这里以存储下三角为例。对于下面的矩阵我们只需要存储对角线和其下面的元素。

那么要存储多少元素？或者一位数组要多大空间？来算一下：
在第一行需要存储1个元素；在第二行需要存储2个元素；在第三行需要存储3个元素；则需要存储1+2+3=6个元素。

每行元素数量递增1，递增到n（n=行数）。那么推广开存储有n行的对称矩阵需要的空间大小是：“1+2+3+…+n-1+n”= n(n+1)/2
现在可以压缩存储元素了

既设置一个结构体变量，存储哪些非零元素的下标和值

再将这些结构体做成一个组，放入另一个结构体——既三元组中

#define SMAX 1000

typedef struct
{
int i,j;
//储存非零元素的行和列信息
datatype v; //非零元素的值

}SPNode;
//定义三元组类型
typedef struct
{
int mu,nu,tu; //矩阵的行、列和非零元素的个数

SPNode data[SMAX]; //三元组表

}SPMatrix；

稀疏矩阵的转置

操作：一个n*m的稀疏矩阵转置后得到的将是一个m*n的矩阵。简单来说就是讲三元组中的行标和列标交换，但是仅仅是这样就结束了么？ 当然不是。前面规定三元组的是按一行一行且每行中的元素是按列号从小到大的规律顺序存放的，因此B 也必须按此规律实现。

 

——>

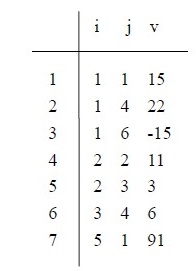算法思路：

①A 的行、列转化成B 的列、行；
②在A.data 中依次找第一列的、第二列的、直到最后一列，并将找到的每个三元组的行、列交换后顺序存储到B.data 中即可。

由于对于A的转置是自上而下的，也就要求对于A中任意元素的转置后位置必须是可知的，而原储存顺序是按行号排列的，所以转置前同列的在前面的转置后一定还在同行的前方。故确定了转置后的每行的第一个元素的位置即确定整个顺序。具体计算如下图

SPMatrix * TransM1 (SPMatrix *A)
{
SPMatrix *B;
int p,q,col;
B=malloc(sizeof(SPMatrix)); /*申请存储空间*/
B->mu=A->nu; B->nu=A->mu; B->tu=A->tu;
/*稀疏矩阵的行、列、元素个数*/
if (B->tu != 0) /*有非零元素则转换*/
{
q=0;
for (col=1; col<=(A->nu); col++)
　　
{ /*按A 的列序转换*/
　　for (p=1; p<= (A->tu); p++) /*扫描整个三元组表*/
　　if (A->data[p].j==col )
　　{
　　B->data[q].i= A->data[p].j ;
　　B->data[q].j= A->data[p].i ;
　　B->data[q].v= A->data[p].v;
　　q++;
　　}/*if*/
　　　
}
} /*if(B->tu>0)*/
return B; /*返回的是转置矩阵的指针*/
} /*TransM1*/

三元组操作（搬运自大佬：原文链接）：

 

/*
*任务描述：针对稀疏矩阵，实现10个基本操作
*
1：建立稀疏矩阵 ；
*
2：输出稀疏矩阵 ；
*
3：转置稀疏矩阵 ；
*
4：稀疏矩阵相加 ；
*
5：稀疏矩阵相减；
*
6：稀疏矩阵相乘 ；
*主要函数：
*
1.void CreateMatrix(Matrix &M);//创建矩阵
*
2.void Output(Matrix M);//输出矩阵
*
3.void TransposeMatrix1(Matrix &M);//转置矩阵算法1
*
4.void TransposeMatrix2(Matrix &M);//转置矩阵算法2
*
5.void TransposeMatrix3(Matrix &M);//转置矩阵算法3
*
6.void AddMatrix(Matrix &M1,Matrix &M2);//矩阵相加
*
7.void SubtractMatrix(Matrix &M1,Matrix &M2);//矩阵相减
*
8.void MultiplyMatrix(Matrix &M,Matrix &N);//矩阵相乘
*
9.Status Check(Matrix M,int index,int row,int line);//检查矩阵M的数组data中第index个元素的行列数
*
10.void SortByRow(Matrix &M);//行优先冒泡排序
*
11.void SortByLine(Matrix &M);//列优先冒泡排序
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<iomanip>
using namespace std;
#define OK 1
#define FALSE 0
#define MAXSIZE 10000
typedef int ElemType;
typedef int Status;
typedef struct
{
int row;//非零元素所在的行
int line;//非零元素所在的列
ElemType elem;//非零元素大小
} Triple;//非零元素的三元组类型

typedef struct
{
Triple data[MAXSIZE];//非零元素数组
int rownum;//矩阵的行数
int linenum;//矩阵的列数
int elemnum;//矩阵的非零元素总数
} Matrix;//矩阵类型
void CreateMatrix(Matrix &M);//创建矩阵
void Output(Matrix M);//输出矩阵
void TransposeMatrix1(Matrix &M);//转置矩阵算法1
void TransposeMatrix2(Matrix &M);//转置矩阵算法2
void TransposeMatrix3(Matrix &M);//转置矩阵算法3
void AddMatrix(Matrix &M1,Matrix &M2);//矩阵相加
void SubtractMatrix(Matrix &M1,Matrix &M2);//矩阵相减
void MultiplyMatrix(Matrix &M,Matrix &N);//矩阵相乘
Status Check(Matrix M,int index,int row,int line);//检查矩阵M的数组data中第index个元素的行列数
void SortByRow(Matrix &M);//行优先冒泡排序
void SortByLine(Matrix &M);//列优先冒泡排序
void Interaction();//输出操作
int main()
{
Interaction();
Matrix M,N;
int operate;
while(cin>>operate)
{
switch(operate)
{
case 0:
return 0;
case 1:
cout<<"请输入创建的稀疏矩阵的行数、列数、非0元素个数：";
cin>>M.rownum>>M.linenum>>M.elemnum;
CreateMatrix(M);
break;
case 2:
Output(M);
break;
case 3:
cout<<"转置矩阵共3种方法，请输入使用的方法序号（1/2/3）：";
cin>>operate;
switch(operate)
{
case 1:
TransposeMatrix1(M);
break;
case 2:
TransposeMatrix2(M);
break;
case 3:
TransposeMatrix3(M);
break;
}
break;
case 4:
INPUT1:
cout<<"请输入创建的稀疏矩阵的行数、列数、非0元素个数：";
cin>>N.rownum>>N.linenum>>N.elemnum;
if(M.rownum!=N.rownum||M.linenum!=N.linenum)
{
cout<<"矩阵相加的前提是两个矩阵的行数列数分别相等。请创建合法的矩阵。n";
goto INPUT1;
}
CreateMatrix(N);
AddMatrix(M,N);
break;
case 5:
INPUT2:
cout<<"请输入创建的稀疏矩阵的行数、列数、非0元素个数：";
cin>>N.rownum>>N.linenum>>N.elemnum;
if(M.rownum!=N.rownum||M.linenum!=N.linenum)
{
cout<<"矩阵相减的前提是两个矩阵的行数列数分别相等。请创建合法的矩阵。n";
goto INPUT2;
}
CreateMatrix(N);
SubtractMatrix(M,N);
break;
case 6:
INPUT3:
cout<<"请输入创建的稀疏矩阵的行数、列数、非0元素个数：";
cin>>N.rownum>>N.linenum>>N.elemnum;
if(M.linenum!=N.rownum)
{
cout<<"矩阵相乘的前提是矩阵1的列数等于矩阵2的行数。请创建合法的矩阵。n";
goto INPUT3;
}
CreateMatrix(N);
MultiplyMatrix(M,N);
break;
default:
cout<<"请输入正确的操作数字！n";
}
}
return 0;
}
void CreateMatrix(Matrix &M)//创建矩阵
{
cout<<"请输入"<<M.elemnum<<"个非0元素的行数、列数（均从1开始）、元素大小：n";
for(int i=1; i<=M.elemnum; i++)
{
cin>>M.data[i].row>>M.data[i].line>>M.data[i].elem;
}
SortByRow(M);//将矩阵的所有非零元素按照行优先的顺序重新排列，便于后续操作
cout<<"创建的稀疏矩阵为：n";
Output(M);
}
void Output(Matrix M)//输出矩阵
{
int index=1;
for(int row=1; row<=M.rownum; row++)
{
for(int line=1; line<=M.linenum; line++)
{
if(Check(M,index,row,line))//检测当前位置是否是非零元素

{
cout<<setw(4)<<M.data[index].elem;
index++;
}
else
{
cout<<setw(4)<<0;
}
}
cout<<endl;
}
}
void TransposeMatrix1(Matrix &M)//转置矩阵算法1
{
//算法描述：因为当前矩阵是行优先的，转置后变成列优先的（相对未转置前）。因此
//枚举列数1——M.linenum，对于每一个列数line，按照原矩阵的顺序遍历一遍所有的非零元素，
//找出列数等于line的非零元素并完成转置该元素。

Matrix T;
T.rownum=M.linenum;
T.linenum=M.rownum;
T.elemnum=M.elemnum;
if(T.elemnum)
{
int index1=1;
for(int line=1; line<=M.linenum; line++)//枚举列数1——M.linenum

{
for(int index2=1; index2<=M.elemnum; index2++)//遍历一遍所有的非零元素

{
if(M.data[index2].line==line)//找出列数等于line的非零元素

{
//转置该元素
T.data[index1].row=M.data[index2].line;
T.data[index1].line=M.data[index2].row;
T.data[index1].elem=M.data[index2].elem;
index1++;
}
}
}
}
M=T;//交接矩阵
cout<<"转置后的稀疏矩阵为：n";
Output(M);
}
void TransposeMatrix2(Matrix &M)//转置矩阵算法2
{
//算法描述：增加两个数组：num[M.linenum+1]与cpot[M.linenum+1]
//num[line]：矩阵M第line列中非零元素的总个数；
//cpot[line]：M中第line列当前非零元素在M.data[]中的下标（初始化为当前列中第一个非零元素的下标）
//遍历一遍原矩阵，对当前遍历到的第index个元素，cpot[M.data[index].line]即为该元素在转置后的矩阵中
//data数组中的下标，一步定位。

Matrix T;
T.rownum=M.linenum;
T.linenum=M.rownum;
T.elemnum=M.elemnum;
if(T.elemnum)
{
int num[M.linenum+1];
memset(num,0,sizeof(num));//初始化num数组
for(int index=1; index<=M.elemnum; index++)//求num数组

{
num[M.data[index].line]++;
}
int cpot[M.linenum+1];
int index=0;
while(num[++index]==0);
cpot[index]=1;//第一个该列中存在非零元素的列数在cpot中的值为1
for(int index2=index+1; index2<=M.linenum; index2++)//递推求cpot数组

{
cpot[index2]=cpot[index2-1]+num[index2-1];
}
for(index=1; index<=M.elemnum; index++)
{
int line=M.data[index].line;
int index1=cpot[line];//直接定位当前元素转置后在新矩阵data数组中的下标
T.data[index1].row=M.data[index].line;
T.data[index1].line=M.data[index].row;
T.data[index1].elem=M.data[index].elem;
cpot[line]++;//更新指示的位置

}
}
M=T;
cout<<"转置后的稀疏矩阵为：n";
Output(M);
}
void TransposeMatrix3(Matrix &M)//转置矩阵算法3
{
//算法描述：不需要开辟新数组的内存，直接按照列优先的原则对
//原矩阵的所有非零元素进行冒泡排序。排序后，对矩阵所有非零元素
//交换行列数，即完成转置。
SortByLine(M);//列优先排序
for(int index=1; index<=M.elemnum; index++)
{
swap(M.data[index].line,M.data[index].row);//交换行列数

}
swap(M.linenum,M.rownum);
cout<<"转置后的稀疏矩阵为：n";
Output(M);
}
void AddMatrix(Matrix &M1,Matrix &M2)//矩阵相加
{
Matrix M;
M.rownum=M1.rownum;
M.linenum=M1.linenum;
int index1=1,index2=1,index=1;
for(int row=1; row<=M.rownum; row++)
{
for(int line=1; line<=M.linenum; line++)
{
if(Check(M1,index1,row,line)&&Check(M2,index2,row,line))
{
M.data[index].elem=M1.data[index1].elem+M2.data[index2].elem;
M.data[index].row=row;
M.data[index].line=line;
index1++;
index2++;
index++;
}
else if(Check(M1,index1,row,line)&&!Check(M2,index2,row,line))
{
M.data[index].elem=M1.data[index1].elem;
M.data[index].row=row;
M.data[index].line=line;
index1++;
index++;
}
else if(!Check(M1,index1,row,line)&&Check(M2,index2,row,line))
{
M.data[index].elem=M2.data[index2].elem;
M.data[index].row=row;
M.data[index].line=line;
index2++;
index++;
}
}
}
M.elemnum=index-1;
M1=M;
Output(M);
cout<<"相加后的矩阵是：n";
Output(M1);
}
void SubtractMatrix(Matrix &M1,Matrix &M2)//矩阵相减
{
Matrix M;
M.rownum=M1.rownum;
M.linenum=M1.linenum;
int index1=1,index2=1,index=1;
for(int row=1; row<=M.rownum; row++)
{
for(int line=1; line<=M.linenum; line++)
{
if(Check(M1,index1,row,line)&&Check(M2,index2,row,line))
{
M.data[index].elem=M1.data[index1].elem-M2.data[index2].elem;
M.data[index].row=row;
M.data[index].line=line;
index1++;
index2++;
index++;
}
else if(Check(M1,index1,row,line)&&!Check(M2,index2,row,line))
{
M.data[index].elem=M1.data[index1].elem;
M.data[index].row=row;
M.data[index].line=line;
index1++;
index++;
}
else if(!Check(M1,index1,row,line)&&Check(M2,index2,row,line))
{
M.data[index].elem=-M2.data[index2].elem;//此处变为其相反数
M.data[index].row=row;
M.data[index].line=line;
index2++;
index++;
}
}
}
M.elemnum=index-1;
M1=M;
cout<<"相减后的矩阵是：n";
Output(M1);
}
void MultiplyMatrix(Matrix &M,Matrix &N)//矩阵相乘
{
//算法描述：先对矩阵N进行列优先排序（M已经为行优先）；
// 在结果矩阵Q可能存在非零元素的情况下：
//枚举Q的每一行row，每一列line，设Q在(row,line)处的值为temp，
//在(row,line)下枚举矩阵M中行数等于row的所有元素M.data[index1]
//在每个M.data[index1]下，枚举列数等于line的矩阵N 中的所有元素N.data[index3]，
//对每个N.data[index3]，当N.data[index3].row等于M.data[index1].line时，两个元素位置匹配相乘即可，
//累加到temp上（temp=temp+N.data[index3].elem*M.data[index1].elem）;
//当前行列(row,line)遍历完成后，temp的值即可求出。
//使用了四个下标：index1，index2，index3，index4
//2和4是辅助更新的下标，详见程序。
SortByLine(N);//对矩阵N进行列优先排序

Matrix Q;
Q.rownum=M.rownum;
Q.linenum=N.linenum;
Q.elemnum=0;
int index=1;
if(M.elemnum*N.elemnum)
{
int index1,index2=1;
//index1是矩阵M的遍历器；
//index2辅助更新M矩阵元素遍历起点，其值为矩阵M中第一个行数等于当前row的元素下标
for(int row=1; row<=Q.rownum; row++)//枚举Q的每一行row

{
int index3,index4=1;
//index3是矩阵N的遍历器；
//index4辅助更新N矩阵元素遍历起点，其值为矩阵N中第一个列数等于当前line的元素下标
for(int line=1; line<=Q.linenum; line++)//每一列line

{
int temp=0;//Q在(row,line)处的值
for(index1=index2;index1<=M.elemnum&&M.data[index1].row==row; index1++)
//在index1不越界且M的第index1个元素在第row行的前提下遍历M的元素

{
for(index3=index4; index3<=N.elemnum&&N.data[index3].line==line; index3++)
//在index3不越界且N的第index3个元素在第line列的前提下遍历N的元素

{
if(M.data[index1].line==N.data[index3].row)//两个元素位置匹配相乘即可

{
temp=temp+M.data[index1].elem*N.data[index3].elem;//累加到temp上

}
}
if(index1==M.elemnum||M.data[index1+1].row!=row)
//当矩阵M的所有在第row行的元素遍历完成一遍后（index1==M.elemnum针对矩阵M的最后一行）

{
index4=index3;
//此时N.data[index3].line=line+1，将该下标值复制到index4中，下次遍历下一列时无需从头开始

}
}
if(temp)
{
Q.data[index].row=row;
Q.data[index].line=line;
Q.data[index].elem=temp;
index++;
}
if(line==Q.linenum)
//当矩阵Q的第row行求值完成后

{
index2=index1;
//此时M.data[index1].row=row+1，将该下标值复制到index2中，下次遍历下一行时无需从头开始

}
}
}
Q.elemnum=index-1;
}
M=Q;
cout<<"相乘后的稀疏矩阵为：n";
Output(M);
}
Status Check(Matrix M,int index,int row,int line)//检查矩阵M的数组data中第index个元素的行列数
{
if(index<=M.elemnum&&M.data[index].row==row&&M.data[index].line==line)
{
return OK;
}
return FALSE;
}
void SortByRow(Matrix &M)//行优先冒泡排序
{
if(M.elemnum)
{
for(int i=1; i<=M.elemnum; i++)
{
for(int j=i+1; j<=M.elemnum; j++)
{
if(M.data[i].row>M.data[j].row||(M.data[i].row==M.data[j].row&&M.data[i].line>M.data[j].line))
{
swap(M.data[i],M.data[j]);
}
}
}
}
}
void SortByLine(Matrix &M)//列优先冒泡排序
{
if(M.elemnum)
{
for(int i=1; i<=M.elemnum; i++)
{
for(int j=i+1; j<=M.elemnum; j++)
{
if(M.data[i].line>M.data[j].line||(M.data[i].line==M.data[j].line&&M.data[i].row>M.data[j].row))
{
swap(M.data[i],M.data[j]);
}
}
}
}
}
void Interaction()//输出操作
{
cout<<"请输入对应操作的序号：n";
cout<<"0：退出程序 ；n";
cout<<"1：建立稀疏矩阵 ；n";
cout<<"2：输出稀疏矩阵 ；n";
cout<<"3：转置稀疏矩阵 ；n";
cout<<"4：稀疏矩阵相加 ；n";
cout<<"5：稀疏矩阵相减；n";
cout<<"6：稀疏矩阵相乘 ；n";
}