概述
本文组织如下：先补充完整群的基本概念中直积与半直积的内容；再引入群表示论。
直积的定义有些拗口，我用自己的语言表述一下，可能不是很数学：将两个群各自的一个群元素
直积群是否构成一个群需要简单的论证，但过于显然不需要论证。特别地指出，直积群的单位元为两个群的单位元的直积，即
我个人选择用一个不严格的但是已经接触过的例子来理解直积的概念：对于一个二粒子系统
这个例子见：
HelgaE：高等量子理论-角动量相关笔记（2）zhuanlan.zhihu.com
直积满足的交换律，意味着两个群的群元之间的乘法关系是对易的，而这里的对易有两种：一是两个群的群元之间的群乘数学上是对易的，也就是真正意义上的
两个群的直积可以构成一个新的群，对应地，从一个群也可以通过直积分解出两个群。
直积因子：如果群G有两个子群
这里的子群
一个简单的例子：二维平面上的矢量相加群，可以分解为一维的x方向的矢量相加群和y方向的矢量相加群，该平面上任何一个二维矢量都可以表示为x方向的矢量和y方向的矢量的直积（也是相加）。这两个一维矢量相加群只有一个公共元素0矢量，为它们的单位元；很显然，也都是二维矢量相加群的不变子群。
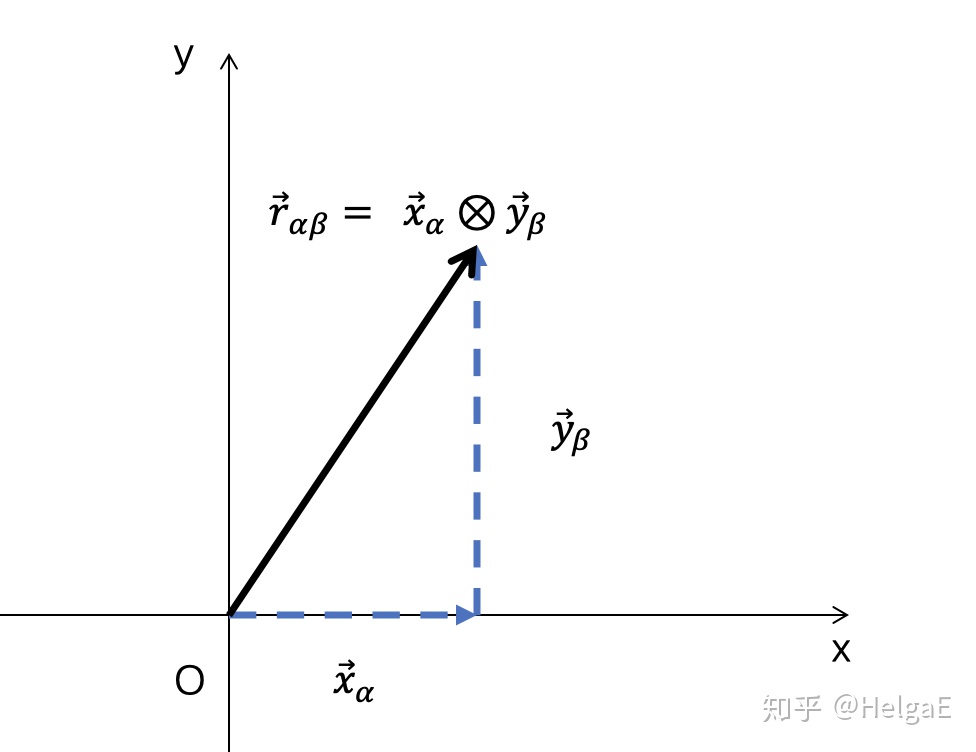
第二个简单的例子，正如前面说过，6阶循环群可以分成
第三个是反例，
半直积：设群
半直积从定义上看很复杂，其重点是构造一个能够把两个群联系在一起且可以形成群乘的关系。群乘做的事是把
半直积群是否构成一个群需要证明：
证明：
封闭性：群乘结果仍为一个与
的有序对，封闭性成立。
结合律：
式子左边为![]()
![]()
注意这里的，代表了
的群元
通过同态映射对应的那个自同构映射。
式子右边为![]()
![]()
![]()
这里第二行到第三行是这样的：，而注意到
与
同态，映射的乘积等于乘积的映射，所以很自然地，
，即证结合律。
单位元：很显然，为。
逆元：，带入验证
。
即证半直积群构成一个群。
两个子群
群表示论需要一些幼儿园级的线性代数知识，在这里只简单写出定义。
线性空间：线性空间又叫向量空间，它是定义在数域K(可以是实数域R，也可以是复数域C)上的向量集合
交换律，
结合律，
单位元为零向量
逆元为
对数乘满足：
这些条件满足的话，V这个向量集合就构成一个线性空间。
线性相关/线性无关：在线性空间V中，任意n个向量
维数：线性空间中线性无关的向量的最大个数m，称为线性空间的维数，记为
基矢：若V是n维线性空间，则V中任意一组n个线性无关的向量可以构成V的一组基矢
线性变换：将线性空间V映入V的映射A，满足
线性变换群：n维复线性空间V上所有非奇异线性变换组成的集合，群乘为依次进行两个线性变换，构成n维复一般线性变换群
n为线性空间的线性变换可以表示为n阶方阵，非奇异的要求是为了保证逆元的存在。一般线性变换群
线性表示：从群G到n维线性空间V上到线性变换群
显然，A的单位元为恒等变换，逆元为互逆的变换。当然，也存在非线性表示，但是这课不讲。线性表示在后面简称为表示。
忠实表示：从群G到n维线性空间V上到线性变换群
接下来是几个例子，便于更好地理解群表示：
1，任何群始终与1（一阶单位矩阵）同态，即1是任何群的表示，称为一维恒等表示，或者显然表示，因为它太显然了，所以一般也不考虑它。
2，任何矩阵群都是自己的忠实表示。这个也很显然。
3，给定以下三个群：
注：这几天知乎的公式编辑器换行出了问题……矩阵弄不出来，只好在本地写出来截图了
一个笛卡尔坐标下的向量
首先单位元E都是一样的，为对应维度（三维）的单位矩阵：
I表示空间反演，即xyz都变相反数：
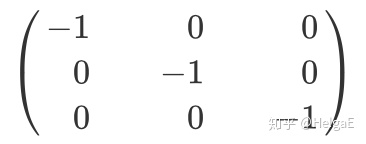
4，对
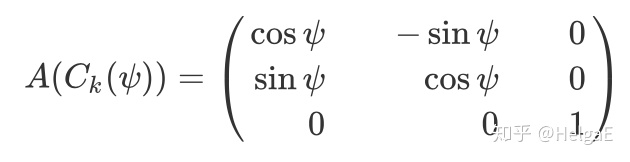
形如这样的矩阵有无数多个（
5，对
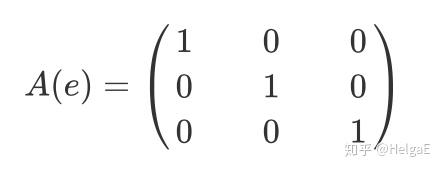
d和f可以用
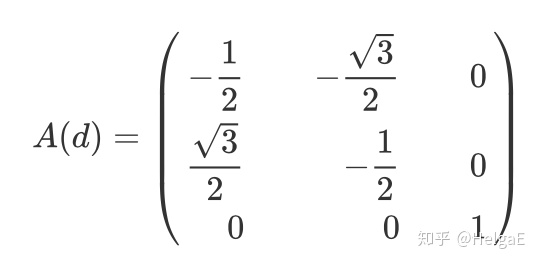
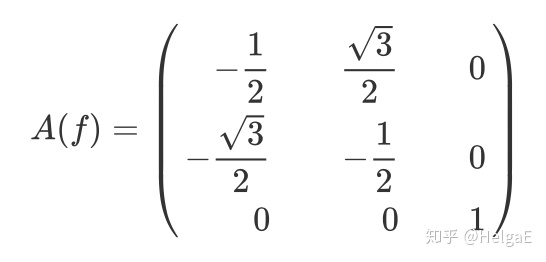
a，b，c求起来比较麻烦，这里提一下思路，以a为例：
首先，虽然这是在三维空间，但实际上这个三角形始终在空间内的xy平面上，z轴坐标恒定不变为0，所以可以写为
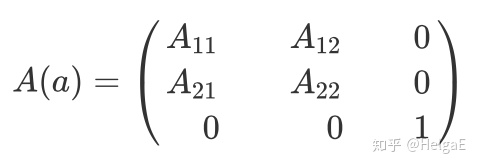
其中
然后按三角形边长为1为例，给出A，B，C三个点的坐标：
然后代入
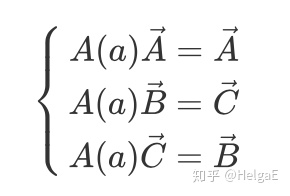
（由于这个矩阵的特殊性，可以简化为二阶矩阵的计算）
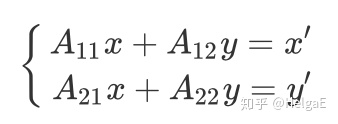
计算过程略，解得：
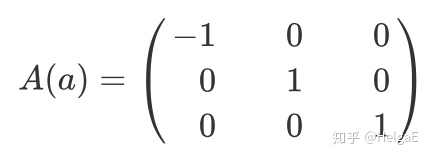
同理，可以解b和c：
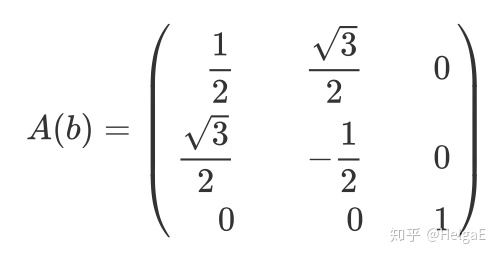
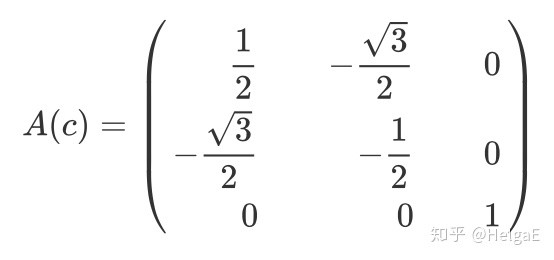
以上就是
给定这样一组基矢：
以e为例，
这个结论很符合直觉，所以可能不是那么有感觉。所以再以a为例：
同理，
最后可以得到，
注：这里与教材上结果不同，是因为我选取了而教材上是-1。
e和a的表示都很简单，接下来再考察复杂一点f：
先算出
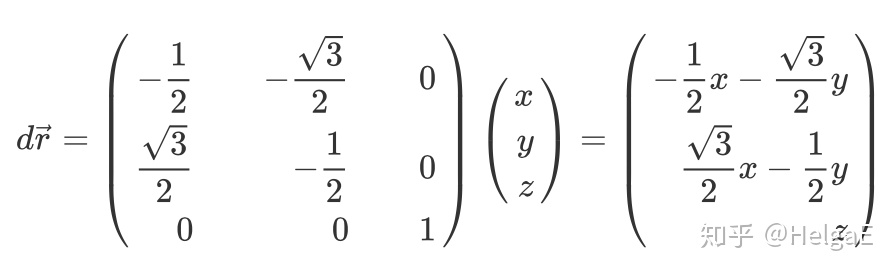
于是可以算出，
得到系数为
为了验证正确性，也给出d：
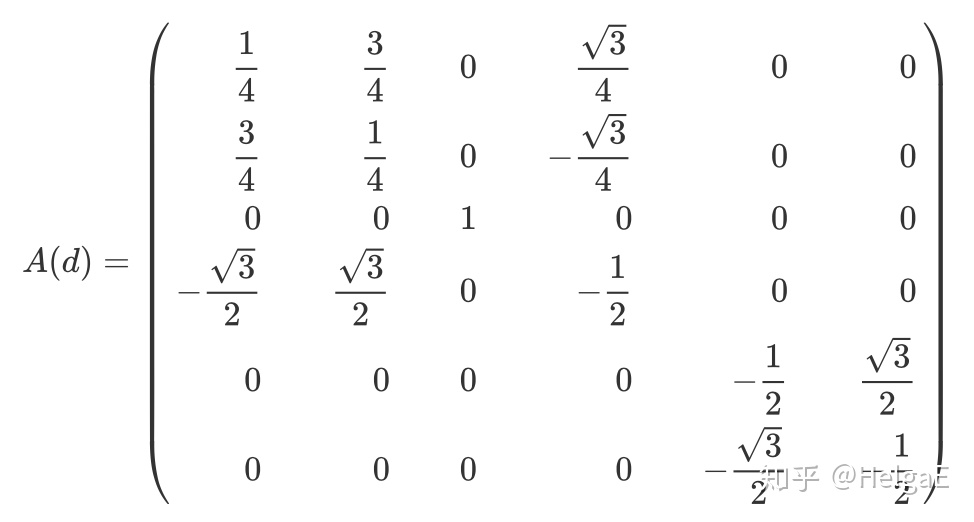
由于在
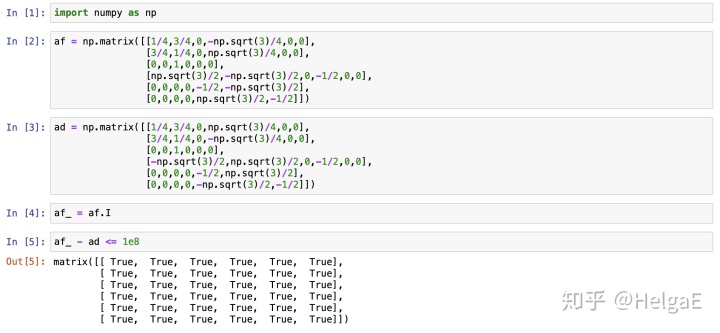
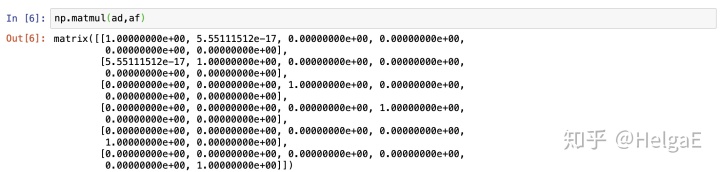
从结果上来看，显然它们是互逆的。
（未完待续…）
最后
以上就是坦率方盒为你收集整理的三元组顺序表表示的稀疏矩阵加法_群论笔记-群表示论（1）的全部内容，希望文章能够帮你解决三元组顺序表表示的稀疏矩阵加法_群论笔记-群表示论（1）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复