卷积神经网络基础知识总结
- 引言
- 卷积层
- 卷积运算与卷积核
- 三维卷积
- 边缘信息丢失?使用Padding填充
- 卷积层的参数与输出维度计算
- 训练时,卷积层要学什么?
- 池化层
- 池化操作
- 池化层的超参数与理解
- 总结
引言
虽然已经阅读过一两本深度学习相关的入门书籍,也看了一些课程,自认为已经打好了基础,但是最近在阅读论文的时候还是发现对CNN的学习中存在很多漏洞和不理解的地方。
因此重新去认真学习了吴恩达大神的课程,并对知识加以梳理。本篇博文主要梳理卷积神经网络的基本知识。有漏洞或者错误之处,欢迎指正,交流的过程就是学习的过程。
卷积层
卷积运算与卷积核
卷积运算是卷积神经网络最重要最基本的运算,用于提取输入图像的特征。
说到卷积运算,先说说卷积核。在不同论文中,卷积核有不同叫法,有的叫核(kernel),有的叫滤波器(filter),实际上都是一种东西。卷积核是一个f×f的矩阵,用于与输入图像或多维数据做卷积运算,n多为奇数,有5×5、3×3等尺寸。在一个卷积层中,卷积核未必只有一个,可能有多个,卷积核的数量也叫作通道数。这时候,每个卷积核分别与输入图像做卷积运算,就会输出多通道特征图。
关于卷积运算的操作方法,简单来说,就是卷积核在输入图像这个窗口内滑动,卷积核覆盖位置上对应元素相乘求和,得到输出图像上对应位置的值。不再详细介绍。要注意的是,卷积层和全连接层一样,也是存在偏置参数的,每个通道进行卷积运算后都需要加上对应通道的偏置量。
必须要提的一点是,在信号处理和某些数学领域,卷积操作的定义中,给出的卷积核不能直接在窗口中滑动运算,而是先进行一个镜像翻转,这时候得到的核才是我们上面所说的卷积核。而上一段简要介绍的跳过镜像翻转的运算操作也被叫做互相关操作(correlation)。现在在很多深度学习的文献或书籍中,习惯于直接把互相关叫做卷积,但是也有保留互相关这一说法的(比如我之前阅读的SiamFC论文)。
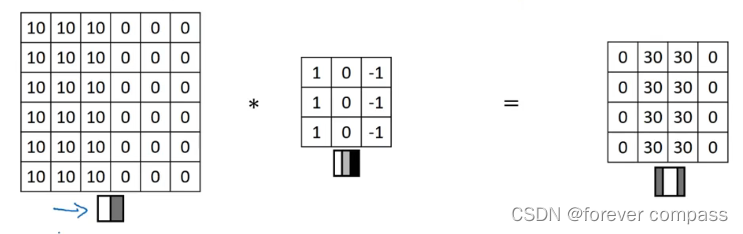
再多说点卷积运算的一点小应用。大家会发现,在图像处理算法中,一些传统边缘检测算法就是采用了卷积运算,采用精心设计的卷积核就可以进行某个轴向上的边缘提取,比如Sobel算法。吴恩达老师给出了一个简单易懂的图例,这里就提取了中间纵向的边缘。
三维卷积
对于三维卷积,同样引用吴恩达老师简单易懂的图来理解:
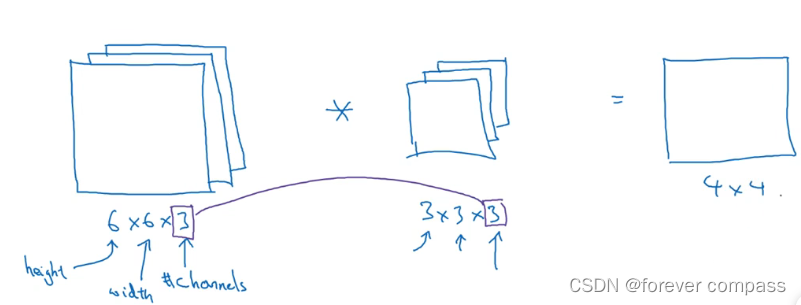
可以看到,对于输入为三通道的一幅输入图像,对应的一个卷积核也是三通道的(不要与前面所说多个卷积核构成多通道输出的通道概念混淆)。input 和kernel对应通道的二维数据各自做卷积运算后,再对三个通道的运算结果求和,最后会输出一幅一通道的二维图像,然后加上该卷积核对应的偏置值。
边缘信息丢失?使用Padding填充
当卷积核沿着输入图像的窗口滑动时,会出现如下问题:
- 图像四角上的像素值只参与了一次运算,图像边缘上的像素利用率也比较低。这样会造成边缘信息的丢失。
- 图像每进行一次卷积,维度都会下降。如果是深层网络,图像的尺寸最终会变得非常小。
因此,在卷积运算之前,采用padding操作对输入图像进行填充,比如在图像外围填充一层全0像素或全1像素,这样在一定程度上就缓解了以上问题,确保图像输入输出尺寸保持稳定,
为了使输入输出图像维度相等,需要计算填充参数。
卷积层的参数与输出维度计算
再补充一下步长(stride)的定义,步长指的是卷积核在窗口中每次卷积之后滑动的步数。
在这里,规定输入图像为n×n,卷积核为f×f,步长为s,padding为p表示填充了p层。
那么就可以给出计算输出图像尺度的通用公式:
(
n
−
f
+
2
p
s
+
1
)
×
(
n
−
f
+
2
p
s
+
1
)
(frac{n-f+2p}{s}+1)×(frac{n-f+2p}{s}+1)
(sn−f+2p+1)×(sn−f+2p+1)
有两种情况:
- 无填充,p=0,按照上述公式计算
- 有填充,一般要求输入输出尺寸一致,这时候通过上述公式来计算p
当 n − f + 2 p s frac{n-f+2p}{s} sn−f+2p不为整数时,向下取整。
训练时,卷积层要学什么?
卷积层的基本知识介绍完了。那么接下来有个问题:训练神经网络的目的是学习参数,更好地预测。在NN中,训练时学习的参数是全连接层的权重和偏置,那么既然CNN中卷积层代替了神经元中的全连接层,卷积层要学习的是哪些参数呢?
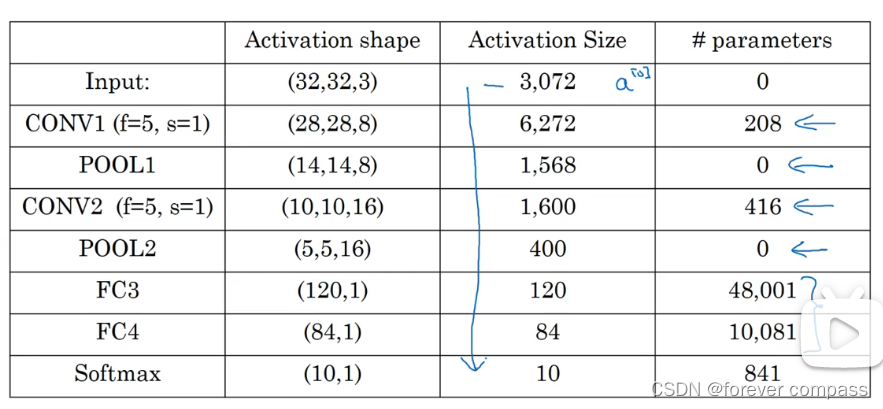
答案是,卷积层需要学习的参数是卷积核的参数和各通道的偏置。为了更好地提取输入图像的特征,需要不断更新卷积核参数。在卷积层中,各通道卷积核的作用类似于全连接层中的权重,但是卷积层要学习的参数数量却通常比全连接层参数数量少的多。如图所示
池化层
CNN的另一个特色结构是池化层(Pooling Layer)。池化层往往不考虑保持输入输出尺度不变,相反,一些经典的CNN结构中使用池化层的目的就是就是为了降维。
池化操作
池化的操作也存在池化核或者池化模板,但是池化模板只会给出一个尺寸,而不是给出一个含具体元素的多维数组。
最常用的池化运算是最大池化,即取池化核覆盖区域内的像素最大值作为新图像对应元素的值。
除此之外,还有平均池化,如其字面意思,但是用的很少。
池化层的超参数与理解
上面说过,池化层的池化核没有具体的值,因此也不需要学习池化核的参数。池化层只有两个超参数:步长s和池化核的尺寸f×f。这两个超参数都是一开始设置好的,不需要学习。基于这一点,往往把一个卷积层和一个池化层放在一起称为一层。
总结
以上,CNN的两种特色结构单元:卷积层和池化层已经介绍完了。在CNN中,通常存在三种层:
- 卷积层CONV
- 池化层POOL
- 全连接层FC
当然了,还有激活函数层如RELU层,不过在很多网络结构中CONV层和FC层是默认包含RELU层的。一些网络的输出部分还有softmax层,但是基本的组成单元还是以上三种。典型的CNN结构包括AlexNet,ResNet50等。
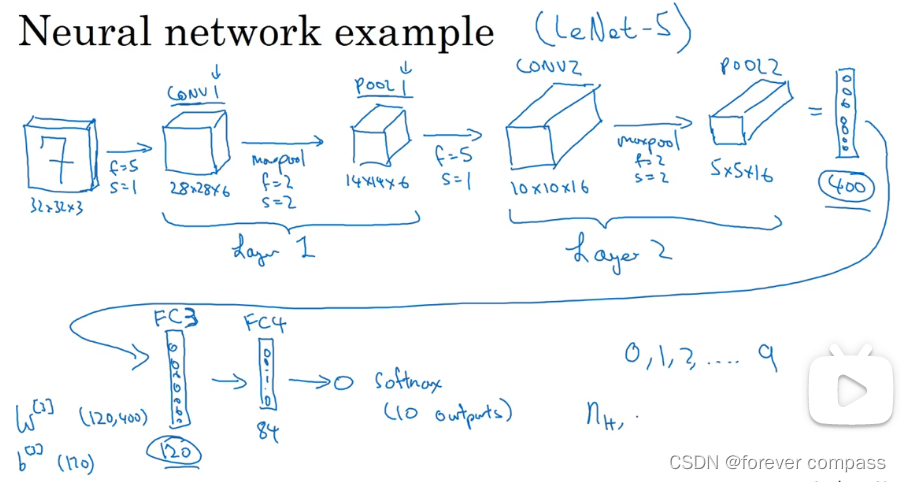
最后放上一个吴恩达老师的结构分析图,可以按照这个图实际算一算,熟悉一下结构和运算。不得不说,老师讲的是真好。
最后
以上就是背后机器猫最近收集整理的关于卷积神经网络基础知识总结引言卷积层池化层总结的全部内容,更多相关卷积神经网络基础知识总结引言卷积层池化层总结内容请搜索靠谱客的其他文章。








发表评论 取消回复