Codeforces Round #744 (Div. 3)题解【A~F】ABCDE1E2F

57 阅读 0 评论 38 点赞

我是靠谱客的博主沉静板凳，最近开发中收集的这篇文章主要介绍Codeforces Round #744 (Div. 3)题解【A~F】ABCDE1E2F，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

A

题意：

给出一个由 A、B、C 三个字母组成的字符串，每次可以删掉一个‘A’一个‘B’，或者一个‘B’一个‘C’，是否能把这个字符串全部删完

题解：

要全部删完，‘A’的数量+‘C’的数量要等于‘B’的数量

#include<iostream>
#include<sstream>
#include<string>
#include<queue>
#include<map>
#include<unordered_map>
#include<set>
#include<vector>
#include<stack>
#include <utility>
#include<list>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<time.h>
#include<random>
using namespace std;
#include<ext/pb_ds/priority_queue.hpp>
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
#include<ext/rope>
using namespace __gnu_cxx;

#define int long long
#define PI acos(-1.0)
#define eps 1e-9
#define lowbit(a) ((a)&-(a))

const int mod = 1e9+7;
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
const int INF = 0x3f3f3f3f;
const int N = 1e6+10;

#define endl 'n'
signed main(){
	std::ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int _; cin>>_;
	while(_--){
		string s; cin>>s;
		int cnta=0,cntb=0,cntc=0,n=s.length();
		for(int i=0;i<n;i++){
			if(s[i]=='A')cnta++;
			else if(s[i]=='B')cntb++;
			else cntc++;
		}
		if(cntb==cnta+cntc)cout<<"YES"<<endl;
		else cout<<"NO"<<endl;
	}
}

B

题意：

给出一个数组a[1…n]，每次可以选择一个区间 $[l, r]$ ，将这个区间的元素都往左移 $d$ 位，这种操作最多执行 $n$ 次，找到一种方案，使数组最后非递减

题解：

既然不需要最小化操作数，那就操作 $n$ 次，第 $i$ 次在区间 $[i . . n]$ 找到最小值的位置 P，然后把区间 $[i . . P]$ 往左移 P-i 个（其实就相当于往右移一个，往右移更好写），即每次都找到剩余元素的最小值并把它放在左边

#include<iostream>
#include<sstream>
#include<string>
#include<queue>
#include<map>
#include<unordered_map>
#include<set>
#include<vector>
#include<stack>
#include <utility>
#include<list>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<time.h>
#include<random>
using namespace std;
#include<ext/pb_ds/priority_queue.hpp>
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
#include<ext/rope>
using namespace __gnu_cxx;

#define int long long
#define PI acos(-1.0)
#define eps 1e-9
#define lowbit(a) ((a)&-(a))

const int mod = 1e9+7;
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
const int INF = 0x3f3f3f3f;
const int N = 1e6+10;
int a[100],b[100];
#define endl 'n'
signed main(){
	std::ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int _; cin>>_;
	while(_--){
		int n; cin>>n;
		vector<pair<int,int>>v;
		for(int i=1;i<=n;i++)cin>>a[i];
		int ans=0;
		for(int i=1;i<=n;i++){
			int p=-1,mi=INF;
			for(int j=i;j<=n;j++)if(a[j]<mi)mi=a[j],p=j;
			if(p==i)continue;//第i位已经是最小的就不用移了
			ans++,v.push_back(make_pair(i,p));
			int tmp=a[p];
			for(int j=p;j>=i;j--)a[j]=a[j-1];
			a[i]=tmp;
		}
		cout<<ans<<endl;
		for(int i=0;i<v.size();i++){
			cout<<v[i].first<<" "<<v[i].second<<" "<<v[i].second-v[i].first<<endl;
		}
	}
}

C

题意：

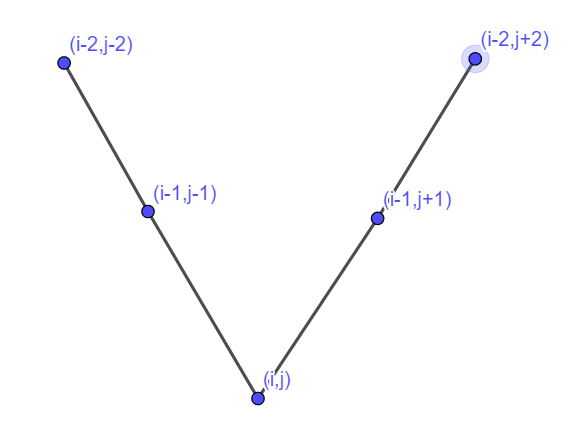
一个n*m的网格，每次可以选择一个点 $(i, j)$ 和一个边长 $d$ ，以 $(i, j)$ 为底部，涂黑一个 V 形，现在给出一个终状态的图和一个边长最小限制K，问这个终状态是否能达到

题解：

枚举终状态每一个被涂黑的点，一直往上找边长的最大延伸，如下图所示
在这里插入图片描述

#include<iostream>
#include<sstream>
#include<string>
#include<queue>
#include<map>
#include<unordered_map>
#include<set>
#include<vector>
#include<stack>
#include <utility>
#include<list>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<time.h>
#include<random>
using namespace std;
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
#include<ext/rope>
using namespace __gnu_cxx;

#define int long long
#define PI acos(-1.0)
#define eps 1e-9
#define lowbit(a) ((a)&-(a))

const int mod = 1e9+7;
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
const int INF = 0x3f3f3f3f;
const int N = 1e6+10;
string s[100];
int vis[100][100];
int n,m,k;
#define endl 'n'
signed main(){
	std::ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int _; cin>>_;
	while(_--){
		memset(vis,0,sizeof vis);
		cin>>n>>m>>k;
		for(int i=0;i<n;i++)cin>>s[i];
		for(int i=0;i<n;i++){
			for(int j=0;j<m;j++){
				if(s[i][j]=='*'){
					int len=0;
					//i,j往上延伸，但是要保证坐标合法，判断左上和右上是不是'*'
					while(i-len>=0&&j-len>=0&&j+len<m&&s[i-len][j-len]=='*'&&s[i-len][j+len]=='*')
						len++;
					len--;//因为(i,j)不计入长度，所以 len要-1
					if(len<k)continue;//往上延伸的距离没达到最小限制就不标记
					for(int u=0;u<=len;u++)
						vis[i-u][j-u]=vis[i-u][j+u]=1;
				}
			}
		}
		int flag=1;
		//如果有涂黑的点但是没被标记过，说明到达不了
		for(int i=0;i<n;i++)
			for(int j=0;j<m;j++)
				if(s[i][j]=='*'&&!vis[i][j])flag=0;
		cout<<(flag?"YES":"NO")<<endl;
	}
}

D

题意：

有 $n$ 个人，第 $i$ 个人的可谈话次数为 $a_i$ ，谈话在两个人之间进行，进行一次对应的可谈话次数 $- 1$ ，求所有人谈话次数总和的最大值，并输出一种方案

题解：
每次必须选a最大的和其他的进行一次谈话，可以从反面想：
假如选的其中一个不是最大的，那么谈到最后，最大值可能有很多次剩余，因为能和最大值谈的都内部消化了，所以最大值必选
这里给两种写法：
优先队列选最大、次大

#include<iostream>
#include<sstream>
#include<string>
#include<queue>
#include<map>
#include<unordered_map>
#include<set>
#include<vector>
#include<stack>
#include <utility>
#include<list>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<time.h>
#include<random>
using namespace std;
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
#include<ext/rope>
using namespace __gnu_cxx;

#define int long long
#define PI acos(-1.0)
#define eps 1e-9
#define lowbit(a) ((a)&-(a))

const int mod = 1e9+7;
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
const int INF = 0x3f3f3f3f;
const int N = 1e6+10;

#define endl 'n'
signed main(){
	std::ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int _; cin>>_;
	while(_--){
		int n; cin>>n;
		priority_queue<pair<int,int>>q;
		for(int i=1;i<=n;i++){
			int x; cin>>x;
			q.push(make_pair(x,i));
		}
		vector<pair<int,int>>v;
		while(1){
			pair<int,int>x=q.top(); q.pop();
			pair<int,int>y=q.top(); q.pop();
			if(x.first==0||y.first==0)break;
			x.first--,y.first--;
			v.push_back(make_pair(x.second,y.second));
			q.push(x); q.push(y);
		}
		cout<<v.size()<<endl;
		for(auto i:v)
			cout<<i.first<<" "<<i.second<<endl;
	}
}

set选最大、最小（显然没第一种好写）

#include<iostream>
#include<sstream>
#include<string>
#include<queue>
#include<map>
#include<unordered_map>
#include<set>
#include<vector>
#include<stack>
#include <utility>
#include<list>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<time.h>
#include<random>
using namespace std;
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
#include<ext/rope>
using namespace __gnu_cxx;

#define int long long
#define PI acos(-1.0)
#define eps 1e-9
#define lowbit(a) ((a)&-(a))

const int mod = 1e9+7;
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
const int INF = 0x3f3f3f3f;
const int N = 1e6+10;

#define endl 'n'
signed main(){
	std::ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	srand(time(0));
	int _; cin>>_;
	while(_--){
		int n; cin>>n;
		vector<pair<int,int>>v;
		set<pair<int,int>>s;
		for(int i=1;i<=n;i++){
			int x; cin>>x;
			if(x)s.insert(make_pair(x,i));
		}
		while(s.size()>1){
			set<pair<int,int>>::iterator it=s.end();it--;
			pair<int,int>x=*s.begin();
			pair<int,int>y=*it;
			if(x.second==0||y.second==0)break;
			v.push_back(make_pair(x.second,y.second));
			x.first--,y.first--;
			s.erase(s.begin());s.erase(it);
			if(x.first>0)s.insert(x);
			if(y.first>0)s.insert(y);
		} 
		cout<<v.size()<<endl;
		for(auto i:v)cout<<i.first<<" "<<i.second<<endl;
	}
}

E1

题意：

给出1~n的排列，模仿deque，只能在头部或者尾部插入元素，求最后字典序最小的序列

题解：

比头部小放头部，否则放尾部

#include<iostream>
#include<sstream>
#include<string>
#include<queue>
#include<map>
#include<unordered_map>
#include<set>
#include<vector>
#include<stack>
#include <utility>
#include<list>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<time.h>
#include<random>
using namespace std;
#include<ext/pb_ds/priority_queue.hpp>
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
#include<ext/rope>
using namespace __gnu_cxx;

#define int long long
#define PI acos(-1.0)
#define eps 1e-9
#define lowbit(a) ((a)&-(a))

const int mod = 1e9+7;
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
const int INF = 0x3f3f3f3f;
const int N = 1e6+10;

#define endl 'n'
signed main(){
	std::ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int _; cin>>_;
	while(_--){
		int n; cin>>n;
		deque<int>q;
		for(int i=1;i<=n;i++){
			int x; cin>>x;
			if(i==1) q.push_front(x);
			else{
				if(x<q.front())q.push_front(x);
				else q.push_back(x);
			}
		}
		while(!q.empty()){
			cout<<q.front()<<" "; q.pop_front();
		}
		cout<<endl;
	}
}

E2

题意：

给出一个序列 $a [1 . . . n]$ ，构造一个序列使逆序对最小（插入方式和deque一样）

题解：

为啥会有这么板子的题。。显然局部最优解就是全局最优解，用树状数组计算当前元素放头部增加的逆序对和放尾部增加的逆序对，选最小的地方插入

#include<iostream>
#include<sstream>
#include<string>
#include<queue>
#include<map>
#include<unordered_map>
#include<set>
#include<vector>
#include<stack>
#include <utility>
#include<list>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<time.h>
#include<random>
using namespace std;
#include<ext/pb_ds/priority_queue.hpp>
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
#include<ext/rope>
using namespace __gnu_cxx;

#define int long long
#define PI acos(-1.0)
#define eps 1e-9
#define lowbit(a) ((a)&-(a))

const int mod = 1e9+7;
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
const int INF = 0x3f3f3f3f;
const int N = 1e6+10;
int a[N],lsh[N];
int c[N],n;
void update(int x,int val){
	for(int i=x;i<=n;i+=lowbit(i)) c[i]+=val;
}
int query(int x){
	int ans=0;
	for(int i=x;i;i-=lowbit(i)) ans+=c[i];
	return ans;
}
#define endl 'n'
signed main(){
	std::ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int _; cin>>_;
	while(_--){
		cin>>n; for(int i=1;i<=n;i++)cin>>a[i],lsh[i]=a[i],c[i]=0;
		sort(lsh+1,lsh+1+n); int m=unique(lsh+1,lsh+1+n)-lsh-1;//离散化
		int ans=0;
		for(int i=1;i<=n;i++){
			int p=lower_bound(lsh+1,lsh+1+m,a[i])-lsh;
			int f=query(p-1),e=query(m)-query(p);
			//f:放头部增加的逆序对 e:放尾部增加的逆序对
			ans+=min(f,e); 
			update(p,1);
		}
		cout<<ans<<endl;
	}
}

F

题意：

给出一个01序列 $a [1 . . . n]$ 和每次右移的距离 $d$ ，每次操作把序列往右移 $d$ 的距离（和B题一样），移完之后 $a [i + d] (新) = a [i] (原) & a [i + d] (原)$ ，即一个数往右移了d个距离后，它的值会变为它的原值 & 这个地方原来的值
求最小需要几次才能让整个序列为0，若无解输出-1

题解：

首先显然，对于一个点，在移动一定的次数后会回到它最初的位置，即它是在一个圈上的
在这里插入图片描述

n=5，d=2时，只有一个圈 1–>3–>5–>2–>4–>1…
在这里插入图片描述

而n=6，d=2时，有两个圈
① 1–>3–>5–>1…
② 2–>4–>6–>2…

显然，当圈里的数有0的时候，圈内的1 & 0 之后会变成 0，到一定次数都会变成 0；
圈里没有0的时候，一直循环下去，圈内的1互相 & ，到最后还是1

所以只要枚举 1 的位置，看它离所在的圈里的 0 需要移动几次就好了

注意，要加个vis数组标记圈内被走过的点，如果每个点都跑一圈会超时，如果一个点被走过，说明之前有个点经过它且比它离 0 更远，它就没必要找了

#include<iostream>
#include<sstream>
#include<string>
#include<queue>
#include<map>
#include<unordered_map>
#include<set>
#include<vector>
#include<stack>
#include <utility>
#include<list>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<time.h>
#include<random>
using namespace std;
#include<ext/pb_ds/priority_queue.hpp>
#include<ext/pb_ds/tree_policy.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
#include<ext/rope>
using namespace __gnu_cxx;

#define int long long
#define PI acos(-1.0)
#define eps 1e-9
#define lowbit(a) ((a)&-(a))

const int mod = 1e9+7;
int qpow(int a,int b){
	int ans=1;
	while(b){
		if(b&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		b>>=1;
	}
	return ans;
}
const int INF = 0x3f3f3f3f;
const int N = 1e6+10;
int a[N],vis[N];
#define endl 'n'
signed main(){
	std::ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int _; cin>>_;
	while(_--){
		int n,d; cin>>n>>d;
		int ans=0,res=1;
		for(int i=0;i<n;i++)cin>>a[i],vis[i]=0;
		for(int i=0;i<n;i++){
			if(vis[i])continue;
			if(a[i]==1){
				int j=(i+d)%n,flag=1,cnt=1;
				while(a[j]==1){
					if(i==j){flag=0; break;}
					//回到了起点还没找到0，说明整个圈都是1
					vis[j]=1,cnt++,j=(j+d)%n;
				}
				if(!flag){res=0;break;}
				else ans=max(ans,cnt);
			}
		}
		if(!res){cout<<-1<<endl; continue;}
		cout<<ans<<endl;
	}
}