“浪潮杯”第九届山东省ACM大学生程序设计竞赛

98 阅读 0 评论 65 点赞

我是靠谱客的博主魁梧帆布鞋，最近开发中收集的这篇文章主要介绍“浪潮杯”第九届山东省ACM大学生程序设计竞赛，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

AAnagram点击查看进入讨论324/620

BBullet点击查看进入讨论56/213 （二分+二分图匹配）

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;
const int maxn=510;
const int INF=0x3f3f3f3f;
int n,vis[maxn],mp[maxn][maxn],tmp[maxn][maxn],link[maxn];
int cnt=0;

bool match(int x){
    for(int i=1;i<=n;i++){
        if(!vis[i]&&tmp[x][i]){
            vis[i]=1;
            if(link[i]==-1||match(link[i])){
                link[i]=x;
                return true;
            }
        }
    }
    return false;
}

int hungry(){
    memset(link,-1,sizeof(link));
    int tot=0;
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        if(match(i))
            tot++;
    }
    return tot;
}

bool check(int x){
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(mp[i][j]<x) tmp[i][j]=0;
            else tmp[i][j]=mp[i][j];
        }
    }

    int res=hungry();
    if(res==cnt) return true;
    else return false;
}

int main(){
    scanf("%d",&n);
    int l=INF,r=-1;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            scanf("%d",&mp[i][j]);
            tmp[i][j]=mp[i][j];
            l=min(l,mp[i][j]);
            r=max(r,mp[i][j]);
        }
    }

    cnt=hungry();  //最多杀害的怪物的数量
    //cout<<"cnt="<<cnt<<endl;
    while(r-l>1){
        int mid=l+(r-l)/2;
        if(check(mid)) l=mid;
        else r=mid;
    }
    printf("%dn",l);
    return 0;
}

CCities点击查看进入讨论581/1259 (贪心，应该本次赛题中难度最低的一个)

题解：注意数据范围10^5*10^5大于整型类型的数据范围（10^9）啦

#include<iostream>
#include<cstdio>
using namespace std;
const int INF=0x3f3f3f3f;
int main()
{
    int t,n,a;
    scanf("%d",&t);
    while(t--){
       long long sum=0,mx=INF;
        scanf("%d",&n);
        for(int i=0;i<n;i++){
            scanf("%d",&a);
            sum+=a;
            if(a<mx)
                mx=a;
        }
        sum+=(n-2)*mx;
        printf("%lldn",sum);
    }
    return 0;
}

DDance点击查看进入讨论26/127 （贪心/树链剖分）

题意：

一个树形结构（根节点是0），给定每个节点的父节点的编号，手轴（hand scroll）个数,从该节点到父节点完成一次升级释放的能量。

升级规则如下：必须从最低层开始，逐层升级，从底层到上一级需消耗一个手轴（hand scroll）才能完成升级，直到升级到最高层，这个时候升级的总能量。

问总能量最大能获得多少？

题解：

模拟样例，样例所对应的树形结构如下

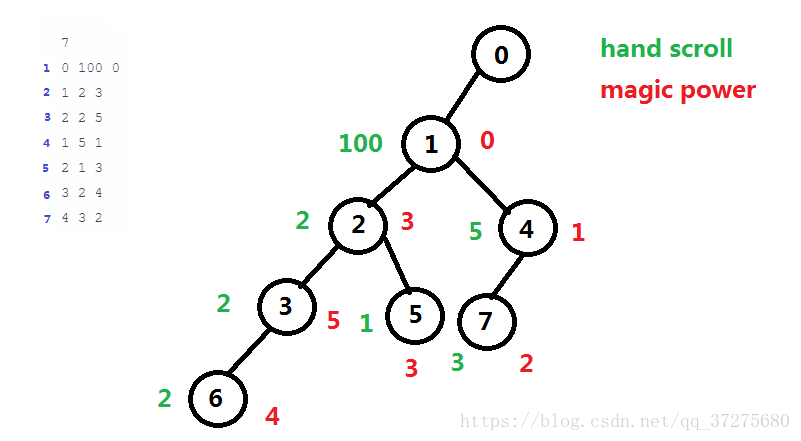
其实，题意明确了之后，很容易看到满足要求的路径总共有三条（从叶节点到根），通过这三条路径完成一次升级所释放的能量也是固定的，到底先让哪条先完成升级呢？

显然，每条路径到底能够升级多少次，受手轴（hand scroll）个数的制约。要想让能量最高，那就先让能量高的路径优先完成升级。

代码：

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
int n,fa[maxn],pre[maxn],num[maxn],power[maxn];
vector<int> son[maxn];
int value[maxn],leaf[maxn],cnt;

/*
dfs()时间复杂度分析：
	对于具有n个顶点、e条边的图来说，dfs算法对图中的每个顶点最多调用一次，因此其递归调用总次数为n。当访问某个
顶点v时，dfs的时间主要花在从该顶点出发查找它的邻接点上。当用邻接表表示图时，需要遍历该顶点的所有邻接点，所有dfs
的总时间为O(n+e);当用邻接矩阵表示图时，需要遍历该顶点行的所有元素，所以dfs的总时间为O(n^2). 
*/

//对于树来说，e=n-1。用邻接表存储树，所以，dfs时间复杂度为O(n) 

void dfs(int id,int w){   //找到叶节点以及每条路径完成每次升级获得到的能量 
	value[id]=w;
	if(son[id].size()==0){
		leaf[cnt++]=id;
		return ;
	}
	int len=son[id].size();
	for(int i=0;i<len;i++){
		int x=son[id][i];
		//printf("power[%d]=%dn",x,power[x]);
		dfs(x,w+power[x]);
	}
}

bool cmp(int a,int b){
	return value[a]>value[b];
}

int previs(int x,int w){
    if(x==0) return w;
    if(num[x]==0)	return 0;
    if(num[x]<w){w=num[x];num[x]=0;}
    else num[x]-=w;
    return previs(fa[x],w);
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",&fa[i],&num[i],&power[i]);
		son[fa[i]].push_back(i);
	}
	
	dfs(0,0); 
	
	/*for(int i=0;i<cnt;i++){
		printf("%d %dn",leaf[i],value[leaf[i]]);
	}*/
	sort(leaf,leaf+cnt,cmp);
	
	ll ans=0;
	int min_num;
	for(int i=0;i<cnt;i++){  //cnt条路径，由路径value[]从大到小进行求能量值 
		int x=leaf[i];
		min_num=previs(x,num[x]); //注意：这里求每段路径的最小手轴数用递归来求，递推的话会超时
		ans+=1ll*min_num*value[x];
	}
	
	/*
	//超时 
	for(int i=0;i<cnt;i++){  //cnt条路径，由路径value[]从大到小进行求能量值 
		int x=leaf[i];
		min_num=num[x];
		int y=fa[x]; 
		while(y){
			min_num=min(min_num,num[y]);
			y=fa[y];
		}
		ans+=1ll*min_num*value[x];
		
		if(min_num){
			y=x;
			while(y){
				num[y]-=min_num;
				y=fa[y];
			}
		}
	}
	
	*/
	
	printf("%lldn",ans);
	return 0;
}

ESequence点击查看进入讨论106/512

FFour-tuples点击查看进入讨论150/722

GGames点击查看进入讨论79/300

HDominoes点击查看进入讨论37/61

IRectangle点击查看进入讨论5/52

JStock点击查看进入讨论0/4