题目描述

解法

双指针定义区间法

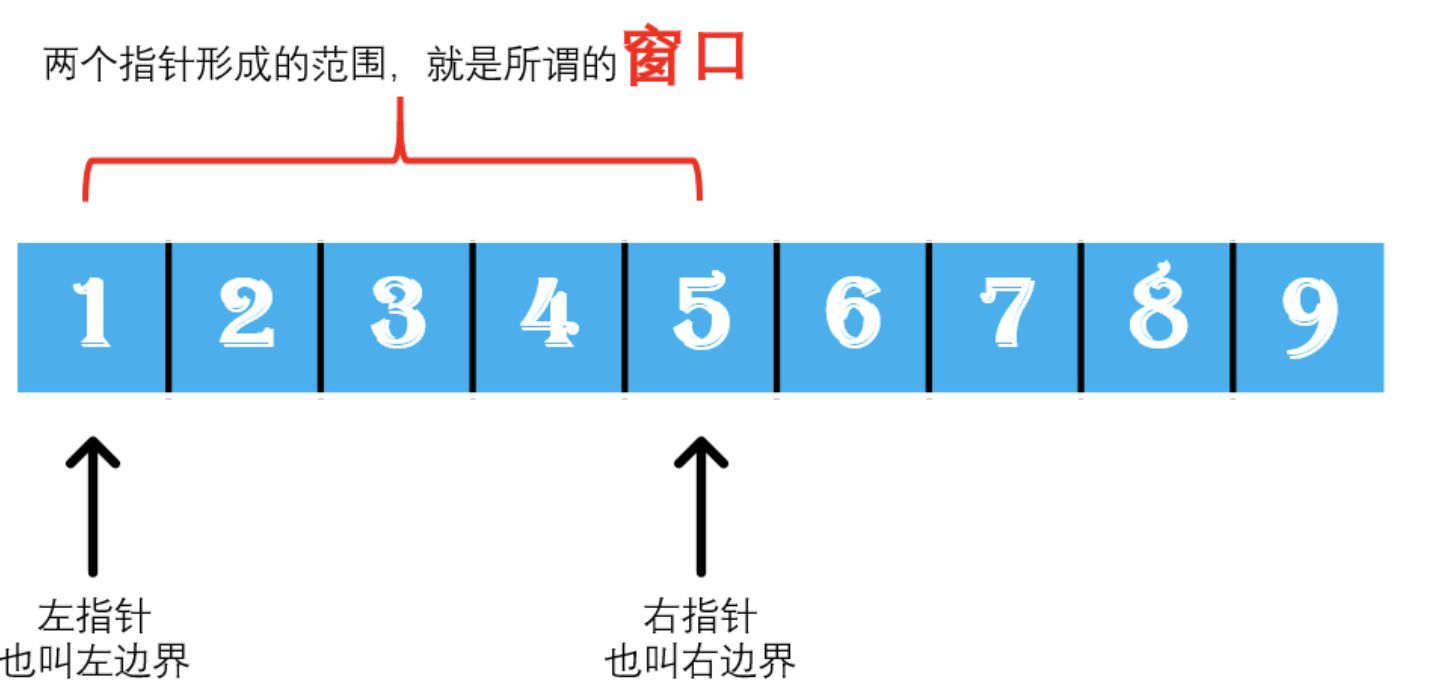
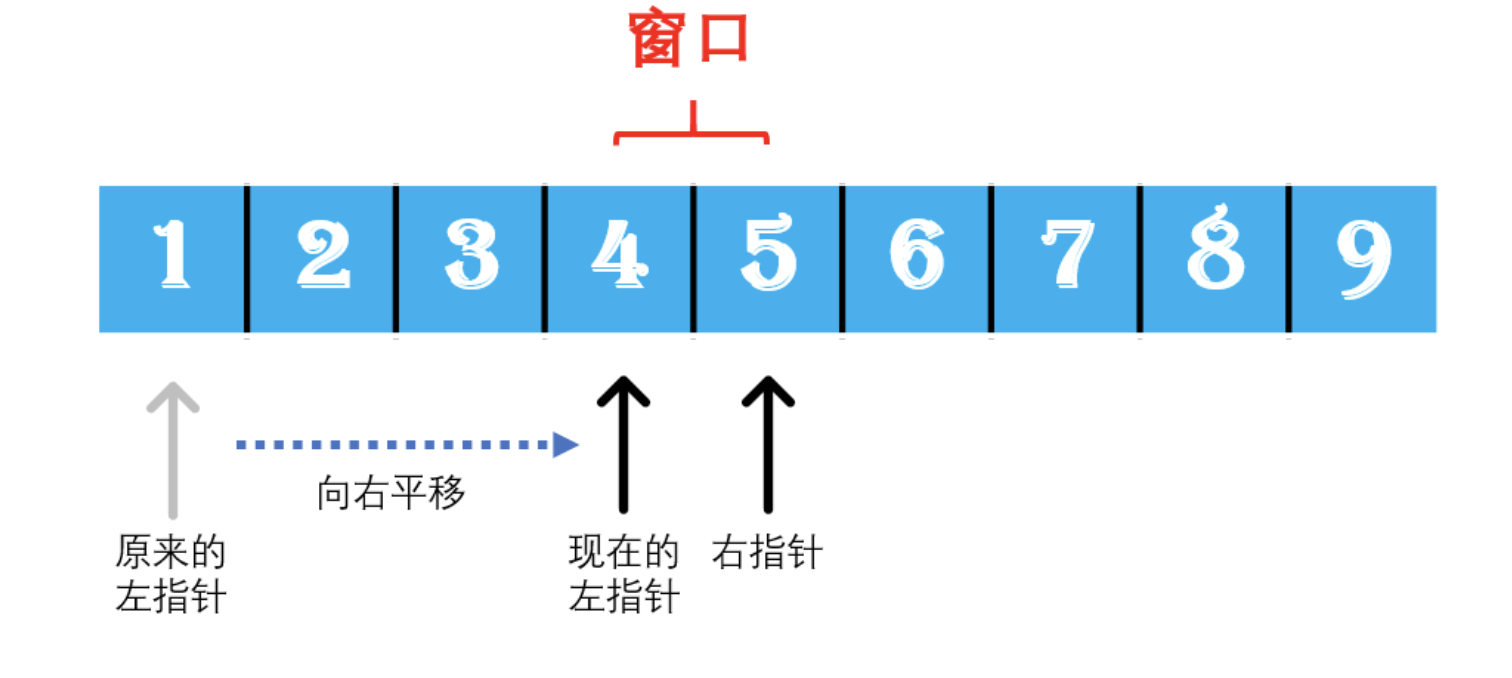
定义两个指针，两个指针窗口内的数字相加。如果加和小于等于target那么右指针向右移一个位置，如果加和大于target，那么左指针向右移一位。

class Solution:
    def findContinuousSequence(self, target: int) -> List[List[int]]:
        i = 1
        j = 1
        result = []
        while i < target and j < target:
            num = sum(list(range(i,j)))
            if num < target:
                j += 1
            elif num > target:
                i += 1
            else:
                result.append(list(range(i,j)))
                j += 1
        return result

利用等差数列加和的方法

由题目叙述可以得到，区间内是一个等差数列，那么可以利用等差数列n项和的原理：$target=\frac{n(a_1+a_n)}{2}$
其中$a_1$是首项，$a_n$是末项，$n$为项数。由于我们的计算中间隔为1，那么可以有$a_n=a_1+n-1$，代入到上面的式子中有：
$$target=\frac{n(a_1+a_1+n-1)}{2}$$
由于target是已知的，那么我们可以得到：
$$a_1=\frac{2target-n(n-1)}{2n}$$
而$$0<n<target$$ $$0<a_1<target$$
因此，我们可以遍历一遍n，并且求出满足条件的整数$a_1$。这样，我们可以写出下面的代码：

class Solution:
    def findContinuousSequence(self, target: int) -> List[List[int]]:
        n = 1
        result = []
        while n < target:
            a1 = (target / n) + (1 - n)/2
            if int(a1)== a1 and a1 > 0 and a1 < target:
                result.append(list(range(int(a1), int(a1) + n)))
            n += 1
        result.sort()
        return result

但是上面，我们漏掉了一个条件$$2target-n(n-1)>0$$，因此可以加上这一项作为一个限定条件，减小计算量：

class Solution:
    def findContinuousSequence(self, target: int) -> List[List[int]]:
        n = 1
        result = []
        while n < target:
            if n*(n-1) >= 2 * target:
                  n += 1
                  continue
            a1 = (target / n) + (1 - n)/2
            if int(a1)== a1 and a1 > 0 and a1 < target:
                result.append(list(range(int(a1), int(a1) + n)))
            n += 1
        result.sort()
        return result
            

思考感想

还是要先考虑数学的方法，多从数学开始思考。

最后

以上就是酷炫故事为你收集整理的剑指offer57:和为s的连续正数序列 python题目描述的全部内容，希望文章能够帮你解决剑指offer57:和为s的连续正数序列 python题目描述所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。