算法刷题重温(十四): 位运算&数学问题(快速幂)&递归小补

71 阅读 0 评论 47 点赞

我是靠谱客的博主从容诺言，最近开发中收集的这篇文章主要介绍算法刷题重温(十四): 位运算&数学问题(快速幂)&递归小补，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 写在前面

今天这篇文章主要是对算法题另外的一些小专题系列进行补充，主要包括位运算，一些数学问题以及递归小补(之前的递归基于树，dfs的偏多，还有一些其他的题目)。先整理一些必备的知识：

位运算
关于位运算，首先要知道是把数字用二进制表示之后，对每一位上0或者1进行的运算，主要包括与、或、异或、左移、右移的操作。前面四种这里就不多说了，而右移操作是个特殊，如果是无符号整数的话，用0填补最左边的 $n$ 位，而如果是有符号整数，则用符号位填补最左边的 $n$ 位。比如如果是一个负数的话10001010, 第一位表示的符号位，那么右移运算时这样： $10001010 > > 3 = 11110001$ ，最左边的 $n$ 位用了符号位1来填充。这个是要注意的。
数学问题
递归
关于递归的话，依然是递归的框架需要默写住

2. 题目梳理和思路总结

2.1 位运算

2.1.1 二进制中1的个数计算思路

这里有个思路非常重要，具体看下面的这是三个题目：

剑指offer15: 二进制中1的个数: 这个题目本身不是很复杂，求1的个数，最直接的思路就是先和1作与运算(这样能看该数二进制的最后一位是不是1)，然后把该数右移一位，重复上面的操作即可。所以第一款代码呼之欲出:

但是这个题还有一种更优雅的做法需要学习一下，因为这种思路可以解很多二进制的问题。那就是n&(n-1), 这个意思就是说把一个整数减去1之后，再和原来的整数做位与运算，得到的结果相当于把整数的二进制表示中最右边的1变成0。这样如果是看一个整数二进制中有多少个1的时候，只需要看看这样的操作能做几次即可。这个思路很重要。这款代码如下：

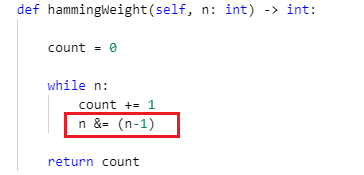
可不要小瞧了框中的这行代码，我们换两个题目，依然是这样的解决思路。
LeetCode231: 2的幂: 这个题目是判断一个整数，是不是2的幂次方，如果某个整数的二进制里面只有一位是1，其他都是0，说明是2的幂次方。所以这个题目还是再考察整数二进制位里面1的个数，所以把上面代码简单修改就可以A掉。核心还是上面那行代码。
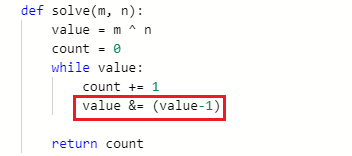
从m到n二进制的改变次数: 这个题是这样的，输入两个整数 $m$ 和 $n$ ，计算需要改变 $m$ 的二进制表示中的多少位才能得到 $n$ 。比如10的二进制1010,13的二进制1101，从10-13，需要改变二进制里面的3位。这个题需要先把 $m$ 和 $n$ 求异或运算，然后统计异或运算结果里面1的个数，就是答案了，所以这个题依然是用到了上面的核心代码。

2.1.2 异或运算及位求和操作

二进制里面的异或运算有时候会起到非常巧妙的作用，首先异或运算的三个性质：

任何一个数与其自己异或的结果都是0，即a^a=0
任何数字和0异或还是它本身，即a^0=a
异或运算有交换律: a^b^c = a^c^b

看几道经典题目：

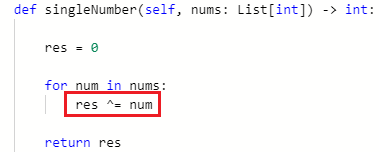
LeetCode136: 只出现一次的数字: 这道题目就是经典的异或运算的解题思路，由于只有一个数字出现了一次，其他数字都是出现了两次，那么我们就就可以直接所有数进行异或运算，这样根据上面异或运算的3条性质，出现两次的数会相互抵消，最后只剩下出现一次的数字。
LeetCode137: 只出现一次的数字II: 这个题对应的是剑指offer56:数组中数字出现的次数II, 准确的说这个其实不是个异或的题目，而是一个位运算中或运算的题目。关键点是其余数字都出现了3次，而只有1个数字出现了一次。这样就说明出现3次的这些数，如果按照二进制位，进行累加的话，结果的每一位是一定可以被3整除的。所以整体思路就是把所有数，按照二进制位对应累加，然后累加结果的每一位都除以3，没法整除的位置设为1，可以整除的位置为0，这时候得到的就是最终只出现一次的结果。这个可以延伸到其余的出现 $n$ 次。

这里学习到的一个知识点， python对于有符号的整数类型和无符号的整数类型是没有区分的，有符号整数类型(int类型)的第31个二进制位是补码意义下的符号位，对应着 $2^{31}$ ，而无符号整数类型由于没有符号，第31个二进制位对应着 $2^{31}$ 。所以对于python来讲，需要对于最高位进行特殊判断。
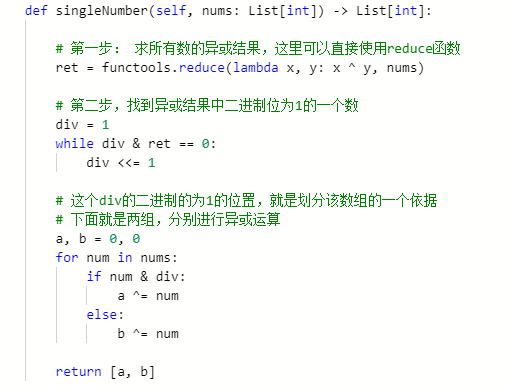
LeetCode260: 只出现一次的数字III: 这个题目对应剑指offer56:数组中数字出现的次数是有两个元素恰好出现一次，其余的都出现2次。所以这个题的核心是先把这个整的数组分成两个数组，而这两个数组满足的是只有一个数出现1次，其余数出现两次，那这时候就转成LeetCode136，进行异或运算就能够找出来。那么如何把这个数组进行划分是关键。思路是这样：
1. 先把所有的数做异或运算，得到异或结果，这里得到的其实是两个出现1次的数的异或
2. 遍历这个异或的结果二进制位，找到为1的一个位置，这个位置说明这两个恰好出现1次的数不同之处，也就是说根据这个位置是否为1进行划分，一定能够将这两个数划分到两个数组中，同时也能保证其他数里面，由于相同的两个数这个位置取值肯定是一样的，那么就保证了出现次数为2的划分后肯定在同一个数组中。
3. 划分完了两个数组之后，对于每个数组做异或运算，最终得到的两个数就是答案。
代码如下：
剑指offer 65: 不用加减乘除做加法: 两位数做加法运算，除了直接相加，就是从位运算的层面做加法。参考后面K神的题解:

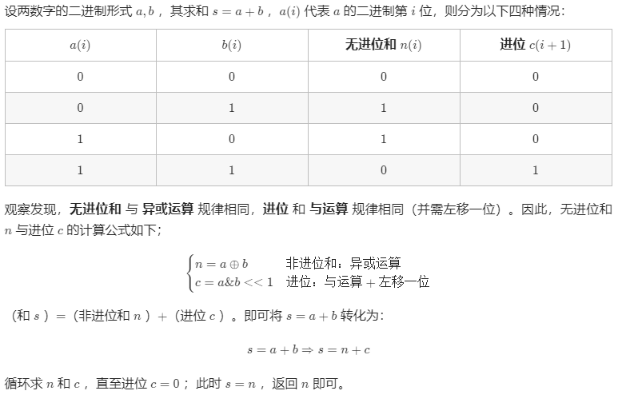
也就是说，两个数先异或运算，然后运算左移1位，然后循环这两两步操作即可。不过python中，数字的特殊存储特点，需要特殊考虑。

python中的负数存储: 参考
Python，Java 等语言中的数字都是以补码形式存储的。但 Python 没有 int , long 等不同长度变量，即在编程时无变量位数的概念。
获取负数的补码：需要将数字与十六进制数 0xffffffff 相与, 可理解为舍去此数字 32 位以上的数字（将 32 位以上都变为 00 ），从无限长度变为一个 32 位整数。
返回前数字还原：若补码 a为负数（ 0x7fffffff 是最大的正数的补码），需执行 ~(a ^ x) 操作，将补码还原至 Python 的存储格式。 a ^ x 运算将 1 至 32 位按位取反； ~ 运算是将整个数字取反；因此， ~(a ^ x) 是将 32 位以上的位取反，1 至 32 位不变。

所以代码如下：

2.2 数学问题

快速幂

剑指offer16: 数值的整数次方：这个题本身的思路不太难，但考察全面性，首先对于输入要分为三种情况
1. 如果底数等于0，指数小于0，此时不合法
2. 如果指数小于0，此时底数要取倒数，然后再算power
3. 正常算power，但是如果是暴力乘，会超时
所以这个题目比较好的一种方式是快速幂的方式，什么意思？比如要求 $x^{11}$ ，如果我们暴力，那就是循环11次，时间复杂度 $O (n)$ ，而快速幂的思想是把11转成二进制数1011，则原来的式子可以转为 $x^{11}=x^{2^3+2^1+2^0}=x^{2^3}times x^{2^1} times x^{2^0}$ ，这时候只算了3次乘积，时间复杂度降为 $O (l o g n)$ 。那么这种方式怎么实现呢？其实是这样，如果我们从n的二进制表示的最右边开始，如果遇到的是1，累乘x，同时 $x * = x$ 进行改变x，比如 $b = 1011$ ，表示 $n = 11$ 的二进制表示，我们从最右边开始，通过与运算 $(b & 1) = = 1$ 来判断最后一位是不是1。如果是1，乘以对应的x，依次累乘即可。
$&x--->x^{2^{0}}--->1\ &x^{2}--->x^{2^{1}}---> 1\ &x^{4}--->x^{2^{2}}---> 0\ &x^{8}--->x^{2^{3}} --->1 end{aligned}$
具体代码如下：
剑指offer 64: 1+2+…n: 这个题如果单单求和的话，思路很多，比如直接有数学公式 $(n + 1) n / 2$ ，或者for循环，或者双指针首尾加等，但是加了限制，不能用for或者if或者乘除法等。那么就需要开阔下思路，而整理的目的也是开阔下思路，for循环运算用递归可以实现，但是递归出口那里，如果不使用if判断，就需要用到另一个策略短路与。也就是只有n大于1的时候，才会进行后面的递归操作。
逻辑运算符的短路效应(后面的K神题解), 常见的逻辑运算符有三种，即 “与 && ”，“或 ||”，“非 ! ” ；而其有重要的短路效应，如下所示：
- if(A && B) // 若 A 为 false ，则 B 的判断不会执行（即短路），直接判定 A && B 为 false
- if(A || B) // 若 A 为 true ，则 B 的判断不会执行（即短路），直接判定 A || B 为 true
本题需要实现 “当 n = 1 时终止递归” 的需求，可通过短路效应实现。
```
n > 1 && sumNums(n - 1) // 当 n = 1 时 n > 1 不成立 ，此时 “短路” ，终止后续递归
```
所以在python中，一句话即可:
```
return n and self.sumNums(n-1) + n
```
这个思路还是非常奇妙的。

2.3 递归小补

这里依然是先上递归模板:

def recursion(level, param1, param2, ...):
	# recursion terminator
	if level > MAX_LEVEL:
		process_result
		return
	
	# process logic in current level
	process(level, data....)
	
	# drill down
	self.recursion(level+1, p1, ...)
	
	# reverse the current level status if needed

下面开始看题:

LeetCode22: 括号生成：这个题如果先想象成有 $2 n$ 个格子，然后每个格子可以任意的添加左括号和右括号，且每一次添充格子之间互不影响，那么每一次填充格子之间的动作就是重复的，就可以使用递归来解决，所以我们可以先简化成先生成所有可能的情况，不考虑有不有效，那么这个问题用递归应该怎么实现呢？

根据上面给出的递归模板，我们来考虑一下这个问题，递归模板里面有三步非常重要
1. 参数：这里的参数需要有当前的level，也就是当前格子， Max_level，也就是最后的格子，还有存放结果的字符串s
2. 递归结束条件：如果当前格子大于最大格子，处理结果结束
3. 处理当前逻辑：当前格子可以加左括号，可以加右括号
4. 带着当前结果进入下一层
根据上面的逻辑，代码如下：
```
def generate(cur_level:1, max_level:2*n, s=''):
	# 终止条件
	if cur_level > max_level:
		print(s)
		return
	
	# 当前逻辑
	s1 = s + '('
	s2 = s + ')'
	
	# 进入下一层
	generate(cur_level+1, max_level, s1)
	generate(cur_level+1, max_level, s2)
```
此时如果再考虑有没有效，可以插入左括号和右括号的条件如下:
- 可以插入左括号：如果当前左括号数目没有达到要求的上限 $n$ ，就可以加
- 可以插入右括号：如果当前右括号的数目没有达到要求的上限 $n$ 且当前右括号的个数小于左括号的个数，才可以加
所以最终代码如下: