140. 单词拆分 II

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，在字符串中增加空格来构建一个句子，使得句子中所有的单词都在词典中。返回所有这些可能的句子。

说明：
分隔时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。

示例：

输入:
s = "catsanddog"
wordDict = ["cat", "cats", "and", "sand", "dog"]
输出:
[
  "cats and dog",
  "cat sand dog"
]

解题思路：动态规划求是否有解、回溯算法求所有具体解。
动态规划得到了原始输入字符串的任意长度的 前缀子串 是否可以拆分为单词集合中的单词；
所有任意长度的前缀是否可拆分是知道的，那么如果 后缀子串在单词集合中，这个后缀子串就是解的一部分
例如：

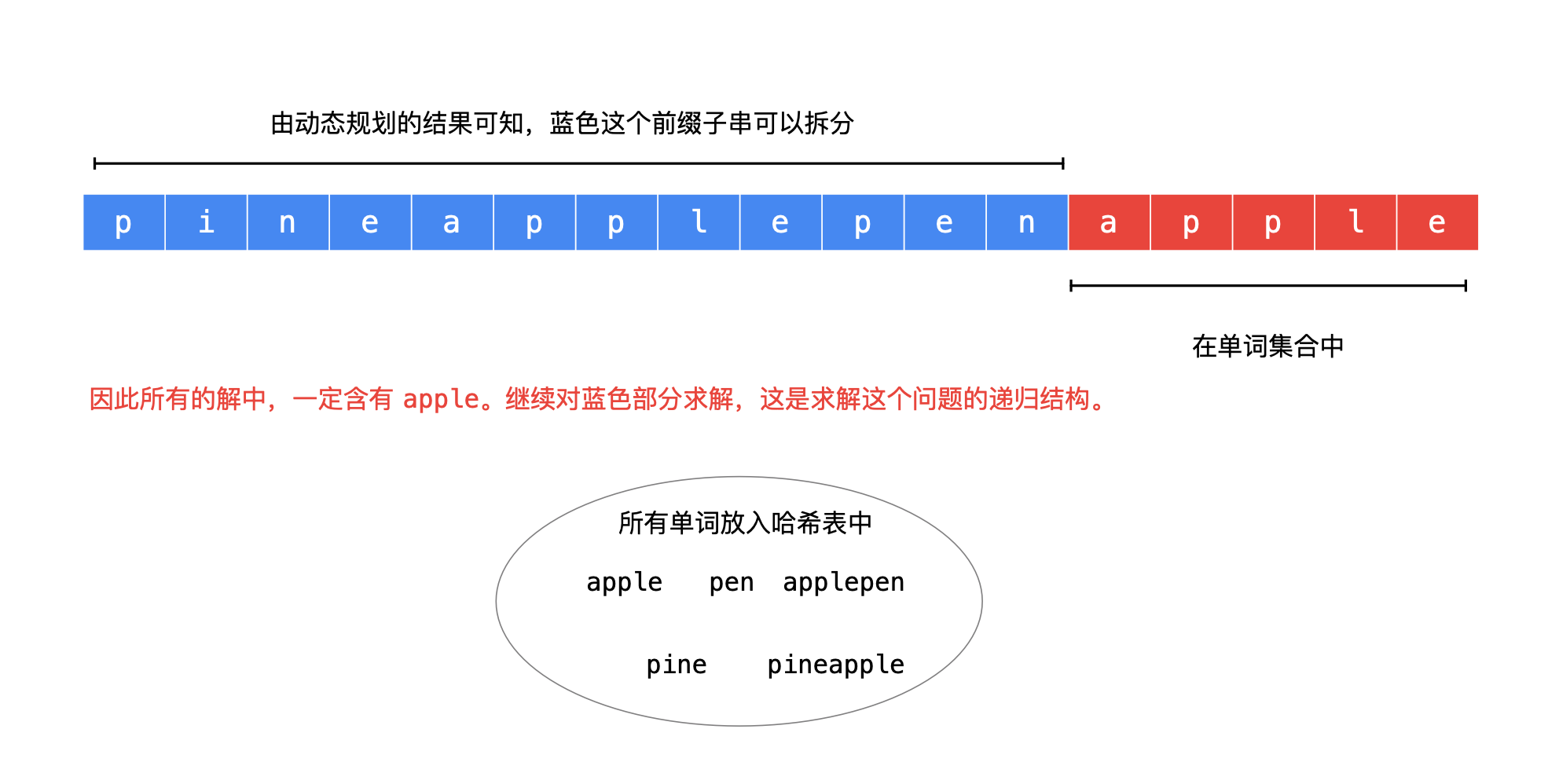
根据这个思路，可以画出树形结构如下。

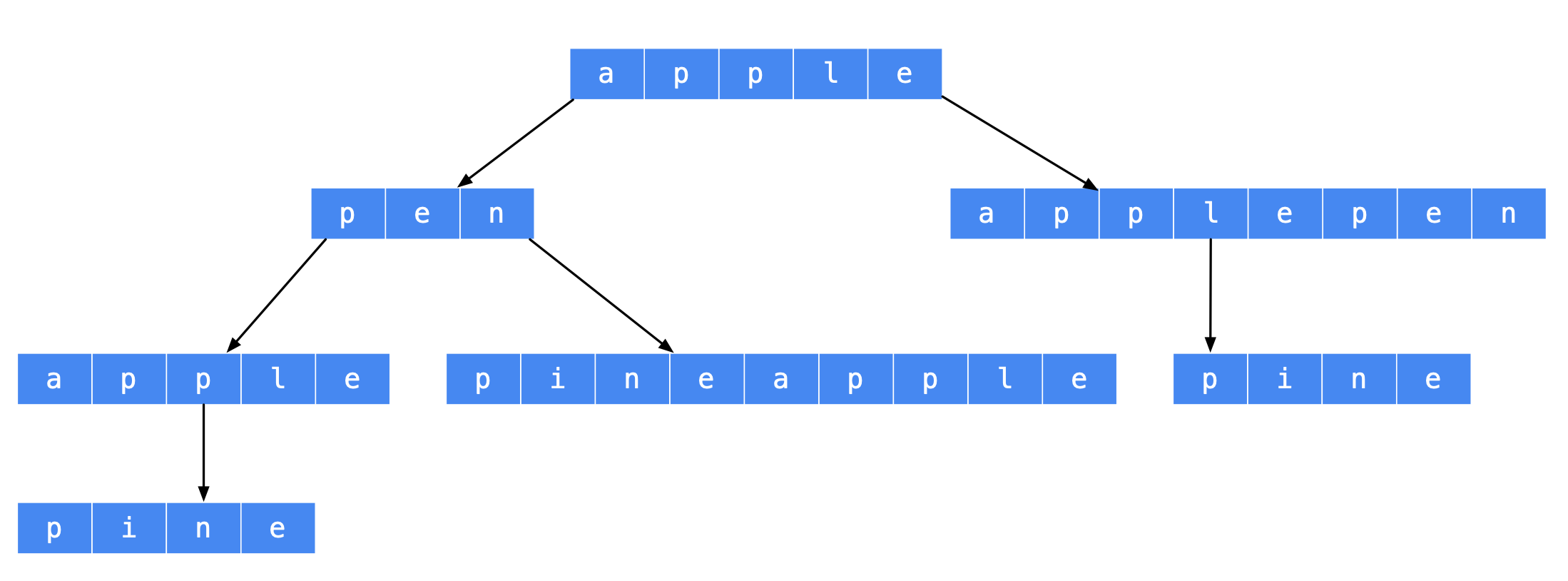
树形结构中，从叶子结点到根结点的路径是符合要求的一个解与以前做过的回溯算法的问题不一样，这个时候路径变量我们需要在依次在列表的开始位置插入元素，可以使用队列（LinkedList）实现，或者是双端队列（ArrayDeque）。

题解来源：
作者：liweiwei1419
链接：https://leetcode-cn.com/problems/word-break-ii/solution/dong-tai-gui-hua-hui-su-qiu-jie-ju-ti-zhi-python-d/
来源：力扣（LeetCode）

public List<String> wordBreak(String s, List<String> wordDict) {
    // 为了快速判断一个单词是否在单词集合中，需要将它们加入哈希表
    Set<String> wordSet = new HashSet<>(wordDict);
    int len = s.length();
    // 动态规划计算是否有解
    // dp[i] 表示「长度」为 i 的 s 前缀子串可以拆分成 wordDict 中的单词
    boolean[] dp = new boolean[len + 1];
    dp[0] = true;
    for (int i = 1; i <= len; i++) {
        for (int j = 0; j < i; j++) {
            if (wordSet.contains(s.substring(j, i)) && dp[j]) {
                dp[i] = true;
                break;
            }
        }
    }
    // 回溯算法搜索所有符合条件的解
    List<String> result = new ArrayList<>();
    if (dp[len]) {
        Deque<String> path = new ArrayDeque<>();
        dfs(s, len, wordSet, dp, path, result);
        return result;
    }
    return result;
}
// 从后往前
// path保存路径的中间结果，result最终结果，len 当前处理的字符串的开始字符下标。
private void dfs(String s, int len, Set<String> wordSet, boolean[] dp, Deque<String> path, List<String> result) {
    if (len == 0) {
        result.add(String.join(" ",path));
        return;
    }
    // 可以拆分的左边界从 len - 1 依次枚举到 0
    for (int i = len - 1; i >= 0; i--) {
        String suffix = s.substring(i, len);
        if (wordSet.contains(suffix) && dp[i]) {
            path.addFirst(suffix);
            dfs(s, i, wordSet, dp, path, result);
            path.removeFirst();
        }
    }
}

141. 环形链表

给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
如果链表中存在环，则返回 true 。 否则，返回 false 。
示例：

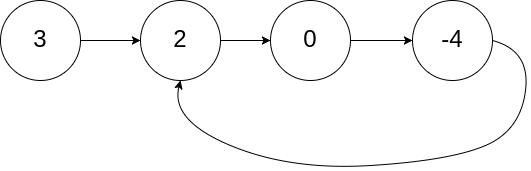
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

方法一：使用哈希表，存储已经访问过的节点。如果再次遇到，说明有环

public boolean hasCycle(ListNode head) {
    HashSet<ListNode> set = new HashSet<>();
    while(head != null){
        if(set.contains(head)){
            return true;
        }
        set.add(head);
        head = head.next;
    }
    return false;
}

方法二：快慢指针，如果有环，则快慢指针一定相遇。

public boolean hasCycle(ListNode head) {
    if (head == null || head.next == null) {
        return false;
    }
    ListNode slow = head;
    ListNode fast = head.next;
    while (slow != fast) {
        if (fast == null || fast.next == null) {
            return false;
        }
        slow = slow.next;
        fast = fast.next.next;
    }
    return true;
}

146. LRU 缓存机制

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制 。
实现 LRUCache 类：

• LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
• void put(int key, int value) 如果关键字已经存在，则变更其数据值；如果关键字不存在，则插入该组「关键字-值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

解题思路：使用哈希表加双链表，来创建一个数据结构，在进行 get 操作，由于使用哈希表，可以在O(1)完成，在 put 操作，最新的元素总是插入到链表头，所以可以在 O(1)完成。
使用链表是为了方便完成删除最近最少使用的元素

// 双向链表
class DoubleLink{
    DoubleLink pre;
    DoubleLink next;
    int val;
    int key;
    DoubleLink(int val,int key){
        this.val = val;
        this.key = key;
        this.next = this.pre = null;
    }
}
// 使用哈希表和双向链表实现
class LRUCache {
	// map存放当前的所有节点
    HashMap<Integer, DoubleLink> map;
    // 最大容量
    int capacity;
    // size 当前节点数量
    int size;
    // 链表的哨兵节点
    DoubleLink head;
    DoubleLink tail;
    // 初始化
    public LRUCache(int capacity) {
        this.capacity = capacity;
        this.size = 0;
        map = new HashMap<>();
        head = new DoubleLink(-1, -1);
        tail = new DoubleLink(-1, -1);
        head.next = tail;
        tail.pre = head;
    }
    // 从当前存储的节点中得到一个元素
    public int get(int key) {
        if (size == 0) {
            return -1;
        }
        // 将访问的元素移动到链表头部
        if (map.containsKey(key)) {
            DoubleLink node = map.get(key);
            // 从链表原位置移除
            node.pre.next = node.next;
            node.next.pre = node.pre;
            // 加入链表头
            nodeToHead(node);
            return node.val;
        }
        return -1;
    }
    // 加入链表和map
    public void put(int key, int value) {
        DoubleLink node;
        // 已经存在key，进行更新 val即可
        if (map.containsKey(key)) {
            // key 已经存在，更新val值
            node = map.get(key);
            node.val = value;
            //从链表中移除
            node.pre.next = node.next;
            node.next.pre = node.pre;
            // 放在链表头部
            nodeToHead(node);
            return;
        }
        // 当前容量已满，删除链表中的最后一个元素
        if (size == capacity) {
            node = tail.pre;
            // 删除双向链表的尾部的元素
            node.pre.next = tail;
            tail.pre = node.pre;
            // 从哈希表中删除
            map.remove(node.key);
            size--;
        }
        // 加入双向链表的头部
        node = new DoubleLink(value, key);
        nodeToHead(node);
        // 加入哈希表
        map.put(key, node);
        size++;
    }
    // 将一个元素移动到链表头部
    private void nodeToHead(DoubleLink node) {
        node.pre = head;
        node.next = head.next;
        head.next.pre = node;
        head.next = node;
    }
}

148. 排序链表

给你链表的头结点 head ，请将其按升序排列并返回排序后的链表 。
进阶：可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？
示例：

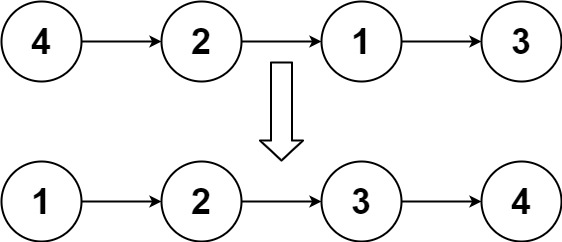
输入：head = [4,2,1,3]
输出：[1,2,3,4]

解题思路：使用归并排序，时间复杂度为 O(nlogn)，递归自顶向下实现，空间复杂度为 O(logn)
归并排序的递归自顶向下实现

public ListNode sortList(ListNode head) {
    return sortList(head,null);
}
public ListNode sortList(ListNode start,ListNode end){
    if(start == end){
        return start;
    }
    // 使用快慢指针，找到链表的中间节点
    ListNode fast,slow;
    fast = start;
    slow = start;
    while(fast != end && fast.next != end){
        fast = fast.next.next;
        slow = slow.next;
    }
    // 以中间节点为界，对两边分别进行排序
    ListNode head1 = sortList(slow.next,end);
    slow.next = null;
    ListNode head2 = sortList(start,slow);
    // 合并两个有序链表，并返回。
    return merge(head1,head2);
}
public ListNode merge(ListNode head1, ListNode head2) {
    ListNode head = new ListNode();
    ListNode p = head;
    while(head1 != null && head2!=null){
        if(head1.val < head2.val){
            p.next = head1;
            p = p.next;
            head1 = head1.next;
        }else{
            p.next = head2;
            p = p.next;
            head2 = head2.next;
        }
    }
    if(head1 != null){
        p.next = head1;
    }
    if(head2 != null){
        p.next = head2;
    }
    return head.next;
}

自底向上归并排序
使用自底向上的方法实现归并排序，则可以达到 O(1) 的空间复杂度。
首先求得链表的长度 length，然后将链表拆分成子链表进行合并。

public ListNode sortList(ListNode head) {
    if(head == null){
        return head;
    }
    // 找到链表的长度
    int length = 0;
    ListNode node = head;
    while(node != null){
        node = node.next;
        length++;
    }
    // dummyHead保存合并后链表的头节点
    ListNode dummyHead = new ListNode(0, head);
    // subLength 合并的节点的个数，自底向上
    for(int subLength = 1;subLength < length; subLength*=2){
        ListNode prev = dummyHead, curr = dummyHead.next;
        while (curr != null) {
        	// 找到第一个要合并的链表头和尾
            ListNode head1 = curr;
            for (int i = 1; i < subLength && curr.next != null; i++) {
                curr = curr.next;
            }
            ListNode head2 = curr.next;
            // 截断第一个链表尾
            curr.next = null;
            // 找到第二个要合并的链表头和尾
            curr = head2;
            for (int i = 1; i < subLength && curr != null && curr.next != null; i++) {
                curr = curr.next;
            }
            // next 保存下一个要合并的起始节点位置
            ListNode next = null;
            if (curr != null) {
                next = curr.next;
                // 截断第二个链表的尾
                curr.next = null;
            }
            // 合并两个找到的链表
            ListNode merged = merge(head1, head2);
            // 将合并好的链表加入 dummyHead链表中
            prev.next = merged;
            while (prev.next != null) {
                prev = prev.next;
            }
            // 从 next的位置进行下一个合并
            curr = next;
        }
    }
    return dummyHead.next;
}
public ListNode merge(ListNode head1, ListNode head2) {
    ListNode head = new ListNode();
    ListNode p = head;
    while(head1 != null && head2!=null){
        if(head1.val < head2.val){
            p.next = head1;
            p = p.next;
            head1 = head1.next;
        }else{
            p.next = head2;
            p = p.next;
            head2 = head2.next;
        }
    }
    if(head1 != null){
        p.next = head1;
    } else{
        p.next = head2;
    }
    return head.next;
}

149. 直线上最多的点数

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
提示：

• 1 <= points.length <= 300
• points[i].length == 2
• -10⁴ <= xi, yi <= 10⁴
• points 中的所有点 互不相同

示例：

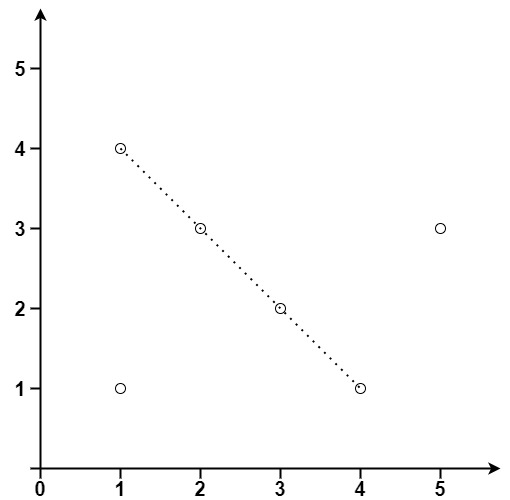
输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

解题思路：遍历每一个坐标点，与其它所有的坐标点，求出斜率，Δy/Δx，注意在程序中不能直接相除，因为浮点数有误差，所以在程序中采用一个 二元组（Δx，Δy）来表示唯一的斜率。要求出 Δx，Δy的最大公约数，将Δy/Δx化简。并使用哈希表存储所有的斜率，并统计在这个斜率中的点数。最后找出斜率中最多的点数。
若 Δx = 0，使 Δy = 1。若 Δy = 0，使 Δx = 1；

public int maxPoints(int[][] points) {
    int length = points.length;
    if (length <= 2) {
        return length;
    }
    int x,y;
    int result = 2;
    // 枚举一个点和其它所有点的斜率
    HashMap<Integer,Integer> map = new HashMap<>();
    for(int i = 0;i < length;i++){
        for(int j = i+1;j<length;j++){
            x = points[i][0] - points[j][0];
            y = points[i][1] - points[j][1];
            // y/x 为斜率，统一处理使得x不为负数
            if (x == 0) {
                y = 1;
            } else if (y == 0) {
                x = 1;
            }else{
                // 使得 x不为负数，统一处理
                if(x < 0){
                    x = -x;
                    y = -y;
                }
                // 对x，y求最大公约数，对斜率化简
                int xyGcd = gcd(Math.abs(x), Math.abs(y));
                x = x/xyGcd;
                y = y/xyGcd;
            }
            // 因为 xi，yi的最大值为10000，所以可以用一个值表示一个（斜率二元组）
            int key = x * 20001 + y;
            //将斜率与斜率上的点数放入哈希表，默认斜率上为一个点，若斜率已经存在于哈希表中，则进行加1处理
            map.put(key, map.getOrDefault(key, 1) + 1);
        }
        // 遍历出斜率中最多的点数
        for(Map.Entry<Integer,Integer> entry:map.entrySet()){
            if(result < entry.getValue()){
                result = entry.getValue();
            }
        }
        map.clear();
    }
    return result;
} 
// 求a,b的最大公约数 
public int gcd(int a, int b) {
    int c;
    c = a % b;
    while(c!=0){
        a = b;
        b = c;
        c = a % b;
    }
    return b;
}

150. 逆波兰表达式求值

根据 逆波兰表示法，求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。
说明：
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。
示例：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

解题思路：使用栈，遇到数字直接入栈，遇到符号，从栈中取出两个数字，计算结果再入栈中。

public int evalRPN(String[] tokens) {
    Stack<Integer> stack = new Stack<>();
    int len = tokens.length;
    for(int i = 0;i<len;i++){
        String s = tokens[i];
        if(!s.equals("+") && !s.equals("-") && !s.equals("*") && !s.equals("/")){
            // 是数字直接入栈
            stack.push(Integer.valueOf(s));
            continue;
        }
        // 是符号，取出栈中的前两个数，进行计算后入栈。
        int right = stack.pop();
        int left = stack.pop();
        switch (s){
            case "+": stack.push(left+right);break;
            case "-": stack.push(left-right);break;
            case "*": stack.push(left*right);break;
            case "/": stack.push(left/right);break;
        }
    }
    return stack.pop();
}

152. 乘积最大子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

示例 :

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

解题思路：动态规划 dp[i]的含义为当前元素作为结尾，所能取得的最大值。由于数组中存在负值，如果当前值nums[i]为负值，nums[i-1]作为元素的结尾所取的最小值，与nums[i]相乘，就有可能比取得的最大值更大。所以不仅仅要记录当前所能取得的最大值，也要记录当前所能取得的最小值。
动态规划的状态转移方程：
dpmax[i] 记录当前取得的最大值。
dpmin[i]记录当前取得的最小值。
dpmax[i] = max(nums[i]，nums[i]*dpmax[i-1]，nums[i]*dpmin[i-1])
dpmin[i] = max(nums[i]，nums[i]*dpmin[i-1]，nums[i]*dpmax[i-1])

如果 dpmax[i] = nums[i] ，dpmin[i] = nums[i]，则说明 当前nums[i]将作为一个新的起始位置，开始寻找乘积的最大值

public int maxProduct(int[] nums) {
    int max, min,ans;
    int tmp1,tmp2;
    max = min = ans = nums[0];
    for(int i = 1; i < nums.length; i++){
        tmp1 = max * nums[i];
        tmp2 = min * nums[i];
        max = Math.max(Math.max(tmp1,tmp2),nums[i]);
        min = Math.min(Math.min(tmp1,tmp2),nums[i]);
        ans = Math.max(ans,max);
    }
    return ans;
}

155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

• push(x) —— 将元素 x 推入栈中。
• pop() —— 删除栈顶的元素。
• top() —— 获取栈顶元素。
• getMin() —— 检索栈中的最小元素。

示例:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

解题思路：使用单链表实现，每次在链表头进行操作，每个链表节点存储当前节点及之前链表节点中的最小值，每次都能从链表头节点得到链表中的最小值。

// 链表节点的结构
class ListNode {
    int val;
    int min;
    ListNode next;
    ListNode() {}
    ListNode(int val,int min, ListNode next) {
        this.val = val;
        this.min = min;
        this.next = next;
    }
}
//栈结构
class MinStack {
	//链表的哨兵节点
    ListNode head;
    public MinStack() {
        head = new ListNode();
    }
    public void push(int val) {
        ListNode node;
        if(head.next == null){
            node = new ListNode(val,val,head.next);
        }else{
        	// 当前节点的min值为之前链表中的最小值与当前值的最小值。
            node = new ListNode();
            node.val = val;
            node.min = Math.min(head.next.min,val);
            node.next = head.next;
        }
        head.next = node;
    }
    public void pop() {
        head.next = head.next.next;
    }

    public int top() {
        return head.next.val;
    }

    public int getMin() {
        return head.next.min;
    }
}

160. 相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。
图示两个链表在节点 c1 开始相交：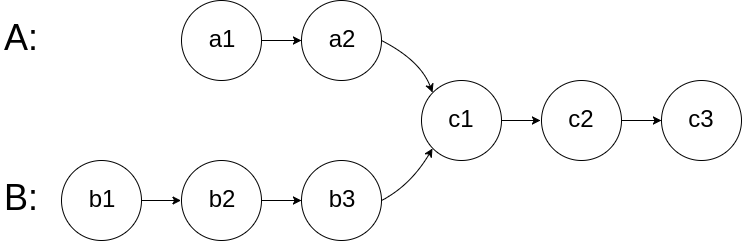
题目数据 保证 整个链式结构中不存在环。
注意，函数返回结果后，链表必须 保持其原始结构 。
示例：

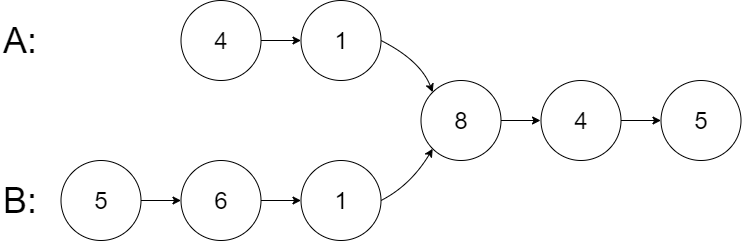
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], 
	 skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

方法一：哈希表
解题思路：先对headA进行遍历，将headA链表中的节点存入哈希表。再对headB进行遍历，遍历时判断哈希表中是否已经存在该节点，存在，则返回。

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    HashSet<ListNode> set = new HashSet<>();
    while(headA != null) {
        set.add(headA);
        headA = headA.next;
    }
    while(headB != null){
        if(set.contains(headB)){
            return headB;
        }
        headB = headB.next;
    }
    return null;
}

方法二：双指针法
链表 A与链表B如果相交，设在 c 处相交，A需要 a步走到 c处，B需要 b步走到 c处，从c处走到 链表尾需要 c步。链表A的长度为 a+c，链表B的长度为 b+c；
如果指针PA从链表A出发，指针 PB从链表B出发，当 PA走到 A的最后一个节点，再从B的头部出发，当 PB走到 B的最后一个节点，再从 A的头部出发。如果存在交点，则当A与B相遇的时候，就是交点。因为 A走到交点的距离 为 a+c+b，B走到交点的距离为 b+c+a。如果没有交点，A，B最终会都为空。

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    ListNode PA,PB;
    PA = headA;
    PB = headB;
    while(PA != PB){
        PA = PA==null?headB:PA.next;
        PB = PB==null?headA:PB.next;
    }
    return PA;
}

162. 寻找峰值

峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
解题思路：一次遍历。时间复杂度为 O(n)不符合题意。可以使用二分查找找到峰值，左指针 l，右指针 r，以其保持左右顺序为循环条件，根据左右指针计算中间位置 m，并比较 m 与 m+1 的值，如果 m 较大，则左侧存在峰值，r = m，如果 m + 1 较大，则右侧存在峰值，l = m + 1。

爬坡思想：总是往高的地方走
如果 nums[i] < nums[i+1]，那么我们抛弃 [l, i] 的范围，在剩余 [i+1, r] 的范围内继续随机选取下标；
如果 nums[i] > nums[i+1]，那么我们抛弃 [i, r] 的范围，在剩余 [l, i-1] 的范围内继续随机选取下标。
时间复杂度为 O(logn)。

public int findPeakElement(int[] nums) {
    int left = 0, right = nums.length - 1;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] > nums[mid + 1]) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left;
}

最后

以上就是无心万宝路为你收集整理的LeetCode面试热题八140. 单词拆分 II141. 环形链表146. LRU 缓存机制148. 排序链表149. 直线上最多的点数150. 逆波兰表达式求值152. 乘积最大子数组155. 最小栈160. 相交链表162. 寻找峰值的全部内容，希望文章能够帮你解决LeetCode面试热题八140. 单词拆分 II141. 环形链表146. LRU 缓存机制148. 排序链表149. 直线上最多的点数150. 逆波兰表达式求值152. 乘积最大子数组155. 最小栈160. 相交链表162. 寻找峰值所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。