leetcode 排序数组十大排序算法实现

66 阅读 0 评论 44 点赞

我是靠谱客的博主火星上大树，这篇文章主要介绍leetcode 排序数组十大排序算法实现，现在分享给大家，希望可以做个参考。

leetcode912. 排序数组十大排序算法实现

文章目录

- leetcode912. 排序数组十大排序算法实现
- - - [912. 排序数组](https://leetcode-cn.com/problems/sort-an-array/)
  - 题目描述
  - 排序算法
  - - 分类
    - 算法复杂度
  - Solution Idea
  - - bubble sort(冒泡排序)
    - Selection sort(选择排序)
    - Insertion sort(插入排序)
    - Shell sort（希尔排序）
    - Merge sort（归并排序）
    - Quick sort（快速排序）
    - Heap sort（堆排序）
    - Count sort（计数排序）
    - Bucket sort（桶排序）
    - Radix sort（基数排序）
    - - Bin sort
      - RadixSort
  - Reference

912. 排序数组

题目描述

给你一个整数数组 nums，请你将该数组升序排列。

Example

复制代码

1
2
3
输入：nums = [5,2,3,1]
输出：[1,2,3,5]

排序算法

算法复杂度

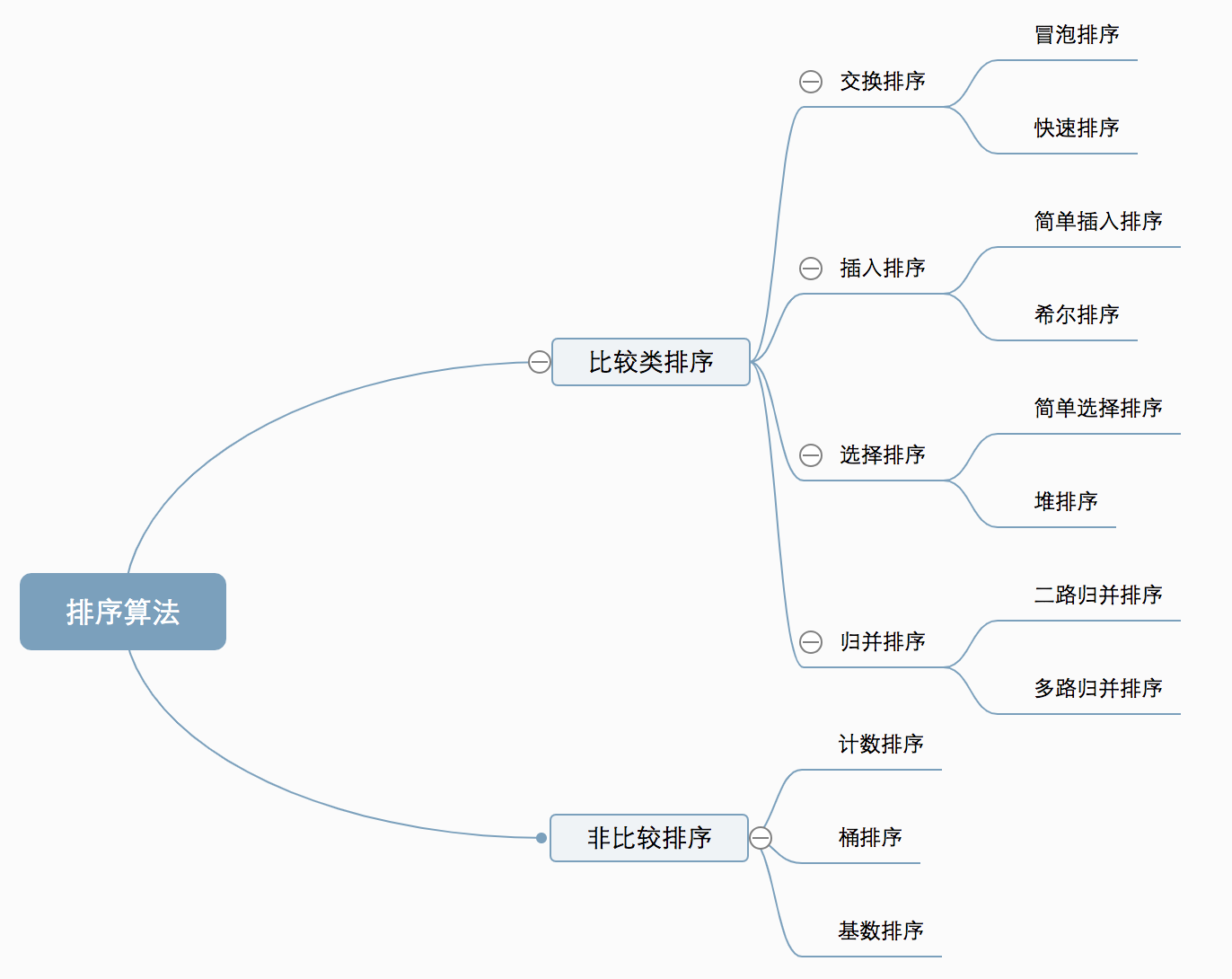
在这里插入图片描述

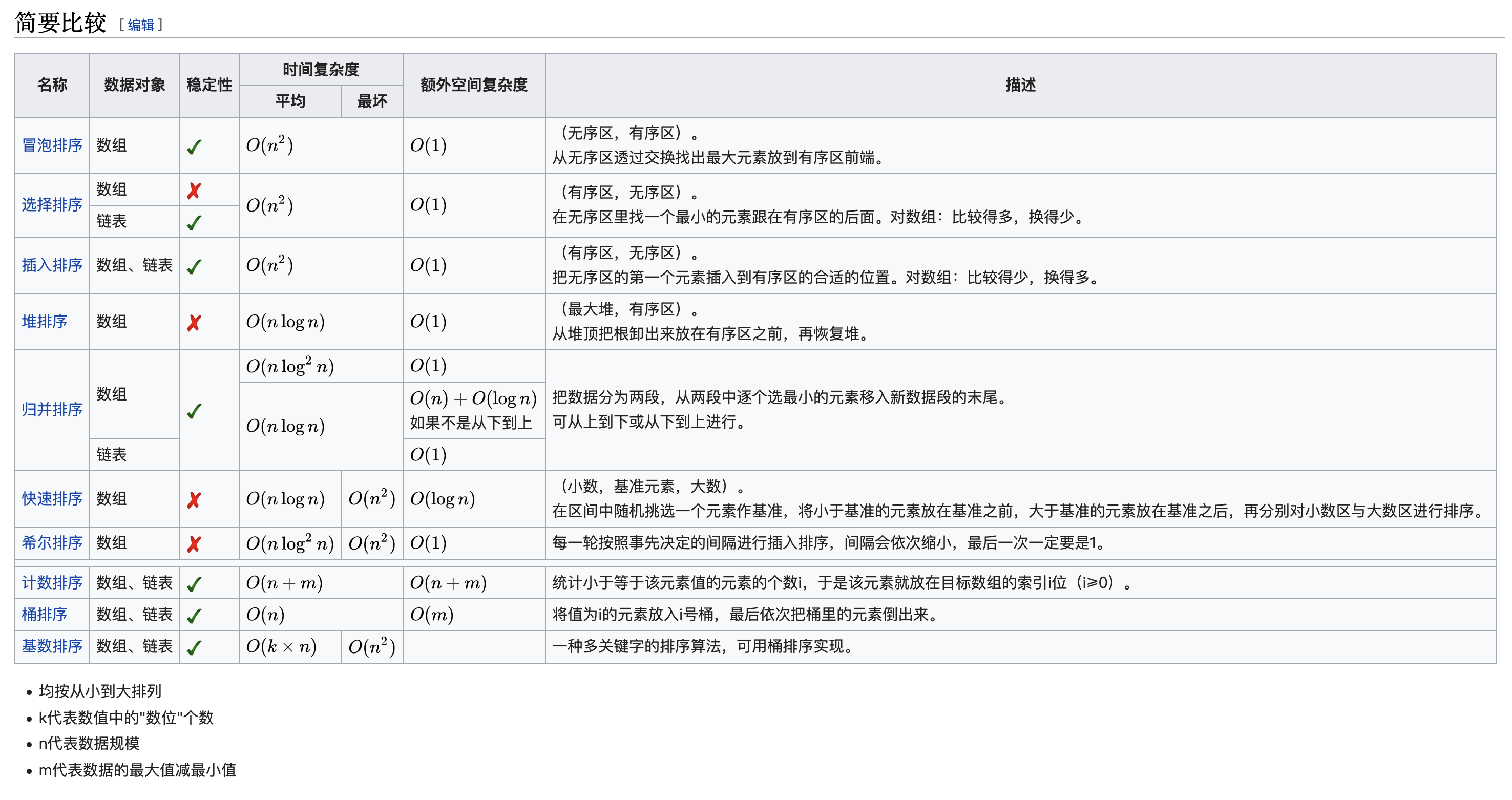
Solution Idea

bubble sort(冒泡排序)

比较相邻的两个数据，如果第二个数小，就交换位置。
从后向前两两比较，一直到比较最前两个数据。最终最小数被交换到起始的位置，这样第一个最小数的位置就排好了。
继续重复上述过程，依次将第2.3…n-1个最小数排好位置。

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/*
** bubble sort 冒泡排序 会超时
*/
class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        if (nums.size() == 1) return nums;
        int tmp;
        bool sorted = true;
        for (int i = 0; i < nums.size() - 1; ++i)
        {
            for (int j = nums.size() - 1; j > i; --j)
            {
                if (nums[j-1] > nums[j])
                {
                    tmp = nums[j-1];
                    nums[j-1] = nums[j];
                    nums[j] = tmp;
                    sorted = false;
                }
            }
            if (sorted) return nums;
        }
        return nums;
    }
};

Selection sort(选择排序)

在长度为N的无序数组中，第一次遍历N-1个数，找到最小的数值与第一个元素交换；

第二次遍历N-2个数，找到最小的数值与第二个元素交换；

…

第N-1次遍历，找到最小的数值与第N-1个元素交换，排序完成。

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    void swap(int& a, int& b)
    {
        int tmp = a;
        a = b;
        b = tmp;
    }
    vector<int> sortArray(vector<int>& nums) {
        if (nums.size() == 1) return nums;
        for (int i = 0; i < nums.size() - 1; ++i)
        {
            int minIndex = i;
            for (int j = i + 1; j < nums.size(); ++j)
            {
                if (nums[i] > nums[j])
                {
                    minIndex = j;
                }
            }
            if (minIndex != i)
            {
                swap(nums[minIndex], nums[i]);
            }
        }
        return nums;
    }
};

Insertion sort(插入排序)

从第一个元素开始，该元素可以认为已经被排序；
取出下一个元素，在已经排序的元素序列中从后向前扫描；
如果该元素（已排序）大于新元素，将该元素移到下一位置；
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
将新元素插入到该位置后；
重复步骤2~5

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        if (nums.size() == 1) return nums;
        for (int i = 1; i < nums.size(); ++i)
        {
            int preIdx = i - 1;
            int curVal = nums[i];
            while(preIdx >= 0 && curVal > nums[preIdx])
            {
                nums[preIdx+1] = nums[preIdx];
                preIdx--;
            }
            nums[preIdex+1] = curVal;
        }
        return nums;
    }
};

Note:

数据序列1： 13-17-20-42-28 利用插入排序，13-17-20-28-42. Number of swap:1;
数据序列2： 13-17-20-42-14利用插入排序，13-14-17-20-42. Number of swap:3;

如果数据序列基本有序，使用插入排序会更加高效。

Shell sort（希尔排序）

在要排序的一组数中，根据某一增量分为若干子序列，并对子序列分别进行插入排序。
然后逐渐将增量减小,并重复上述过程。直至增量为1,此时数据序列基本有序,最后进行插入排序。

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int length = nums.size();
        if (length == 1) return nums;
        int inc = length;
        while (true)
        {
            inc /= 2;
            for (int k = 0; k < inc; ++k)
                for (int i = k + inc; i < length; i += inc)
                {
                    int preIdx = i - inc;
                    int curVal = nums[i];
                    while (preIdx >= 0 && curVal < nums[preIdx])
                    {
                        nums[preIdx+inc] = nums[preIdx];
                        preIdx -= inc;
                    }
                    nums[preIdx+inc] = curVal;
                }
            if (inc == 1) break;
        }
        
        return nums;
    }
};

Merge sort（归并排序）

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

把长度为n的输入序列分成两个长度为n/2的子序列；
对这两个子序列分别采用归并排序；
将两个排序好的子序列合并成一个最终的排序序列。

复制代码

class Solution {
    vector<int> nums;
public:
    void merge(int left, int right)
    {
        if (left >= right)
        {
            return ;
        } 
        int mid = (left + right) / 2;
        merge(left, mid);
        merge(mid + 1, right);
        int i = left, j = mid + 1;
        vector<int> tmp;
        while (i <= mid && j <= right)
        {
            if (nums[i] < nums[j])
            {
                tmp.push_back(nums[i]);
                i++;
            }
            else
            {
                tmp.push_back(nums[j]);
                j++;
            }
        }
        while (i <= mid)
        {
            tmp.push_back(nums[i]);
            i++;
        }
        while (j <= right)
        {
            tmp.push_back(nums[j]);
            j++;
        }
        for (i = 0; i < right - left + 1; ++i) nums[i + left] = tmp[i];
    }
    vector<int> sortArray(vector<int>& nums) {
        this -> nums = nums;
        int length = nums.size();
        if (length == 1) return nums; 
        merge(0, nums.size() - 1); // 左闭右闭
        return this -> nums;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    vector<int> nums;
public:
    void merge(int left, int right)
    {
        if (left >= right)
        {
            return ;
        } 
        int mid = (left + right) / 2;
        merge(left, mid);
        merge(mid + 1, right);
        int i = left, j = mid + 1;
        vector<int> tmp;
        while (i <= mid && j <= right)
        {
            if (nums[i] < nums[j])
            {
                tmp.push_back(nums[i]);
                i++;
            }
            else
            {
                tmp.push_back(nums[j]);
                j++;
            }
        }
        while (i <= mid)
        {
            tmp.push_back(nums[i]);
            i++;
        }
        while (j <= right)
        {
            tmp.push_back(nums[j]);
            j++;
        }
        for (i = 0; i < right - left + 1; ++i) nums[i + left] = tmp[i];
    }
    vector<int> sortArray(vector<int>& nums) {
        this -> nums = nums;
        int length = nums.size();
        if (length == 1) return nums; 
        merge(0, nums.size() - 1); // 左闭右闭
        return this -> nums;
    }
};

Quick sort（快速排序）

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

从数列中挑出一个元素，称为“基准”（pivot）；
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

复制代码

/*
** quick sort
*/
class Solution {
public:
    int partion(vector<int>& nums, int left, int right)
    {
        int pivot = nums[right]; //选取尾端元素为基准
        int i = left, j; // i,j 双指针. i 前向指针，j后向指针
        for (j = left; j < right; ++j)
        {
            if (nums[j] <= pivot)
            {
                swap(nums[i], nums[j]);
                i++;
            }
        }
        swap(nums[i], nums[right]); // 从 left 至位置 i都是小于等于 基准元素的数， i位置是基准元素
        return i;
    }
    int random_partion(vector<int>& nums, int left, int right)
    {
        int randIdx = rand() % (right - left + 1) + left; //随机选取基准
        swap(nums[randIdx], nums[right]);
        return partion(nums, left, right);
    }
    void random_quick_sort(vector<int>& nums, int left, int right)
    {
        if (left < right)
        {
            int pivot = random_partion(nums, left, right);
            random_quick_sort(nums, left, pivot - 1);
            random_quick_sort(nums, pivot+1, right);
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        int length = nums.size();
        if (length == 1) return nums; 
        srand (time(NULL));
        random_quick_sort(nums, 0, length - 1); // 左闭右闭区间
        return nums;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*
** quick sort
*/
class Solution {
public:
    int partion(vector<int>& nums, int left, int right)
    {
        int pivot = nums[right]; //选取尾端元素为基准
        int i = left, j; // i,j 双指针. i 前向指针，j后向指针
        for (j = left; j < right; ++j)
        {
            if (nums[j] <= pivot)
            {
                swap(nums[i], nums[j]);
                i++;
            }
        }
        swap(nums[i], nums[right]); // 从 left 至位置 i都是小于等于 基准元素的数， i位置是基准元素
        return i;
    }
    int random_partion(vector<int>& nums, int left, int right)
    {
        int randIdx = rand() % (right - left + 1) + left; //随机选取基准
        swap(nums[randIdx], nums[right]);
        return partion(nums, left, right);
    }
    void random_quick_sort(vector<int>& nums, int left, int right)
    {
        if (left < right)
        {
            int pivot = random_partion(nums, left, right);
            random_quick_sort(nums, left, pivot - 1);
            random_quick_sort(nums, pivot+1, right);
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        int length = nums.size();
        if (length == 1) return nums; 
        srand (time(NULL));
        random_quick_sort(nums, 0, length - 1); // 左闭右闭区间
        return nums;
    }
};

复杂度分析

时间复杂度：基于随机选取主元的快速排序时间复杂度为期望 $O (n lo g n)$ ，其中 n 为数组的长度。详细证明过程可以见《算法导论》第七章，这里不再大篇幅赘述。
空间复杂度：O(h)，其中 h 为快速排序递归调用的层数。我们需要额外的 O(h) 的递归调用的栈空间，由于划分的结果不同导致了快速排序递归调用的层数也会不同，最坏情况下需 O(n) 的空间，最优情况下每次都平衡，此时整个递归树高度为 $lo g n$ ，空间复杂度为 O(log n)。

Note

srand Initialize random number generator.

复制代码

1
2
srand (time(NULL));

rand Generate random number

复制代码

1
2
v1 = rand() % 100;         // v1 in the range 0 to 99

复制代码

1
2
randIdx = rand() % (right - left + 1) + left; //随机选取基准

Heap sort（堆排序）

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

思想就是先将待排序的序列建成 （大根堆）最大堆，使得每个父节点的元素大于等于它的子节点。此时整个序列最大值即为堆顶元素，我们将其与末尾元素交换，使末尾元素为最大值，然后再调整堆顶元素使得剩下的 n-1个元素仍为大根堆，再重复执行以上操作我们即能得到一个有序的序列。

将初始待排序关键字序列(R1,R2….Rn)构建成大跟堆，此堆为初始的无序区；
将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

复制代码

class Solution {
public:
    void make_max_heap(vector<int>& nums, int len)
    {
        for (int i = (len / 2); i >= 0; --i) max_heap_fixed(nums, i, len);
    }
    void max_heap_fixed(vector<int>& nums, int cur_idx, int len)
    {
        int lchild = (cur_idx << 1) + 1, rchild = (cur_idx << 1) + 2;
        while (lchild <= len)
        {
            int large = cur_idx;
            if (lchild <= len && nums[lchild] > nums[cur_idx])
            {
                large = lchild;
            }
            if (rchild <= len && nums[rchild] > nums[large])
            {
                large = rchild;
            }

if (large != cur_idx) 
            {
                swap(nums[cur_idx], nums[large]);
                cur_idx = large;
                lchild = (cur_idx << 1) + 1;
                rchild = (cur_idx << 1) + 2;
            }
            else break;   
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        int length = nums.size() - 1;
        make_max_heap(nums, length);
        for(int i = length; i > 0; --i)
        {
            swap(nums[0], nums[i]);
            max_heap_fixed(nums, 0, i-1);
        }  
        return nums;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
public:
    void make_max_heap(vector<int>& nums, int len)
    {
        for (int i = (len / 2); i >= 0; --i) max_heap_fixed(nums, i, len);
    }
    void max_heap_fixed(vector<int>& nums, int cur_idx, int len)
    {
        int lchild = (cur_idx << 1) + 1, rchild = (cur_idx << 1) + 2;
        while (lchild <= len)
        {
            int large = cur_idx;
            if (lchild <= len && nums[lchild] > nums[cur_idx])
            {
                large = lchild;
            }
            if (rchild <= len && nums[rchild] > nums[large])
            {
                large = rchild;
            }

            if (large != cur_idx) 
            {
                swap(nums[cur_idx], nums[large]);
                cur_idx = large;
                lchild = (cur_idx << 1) + 1;
                rchild = (cur_idx << 1) + 2;
            }
            else break;   
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        int length = nums.size() - 1;
        make_max_heap(nums, length);
        for(int i = length; i > 0; --i)
        {
            swap(nums[0], nums[i]);
            max_heap_fixed(nums, 0, i-1);
        }  
        return nums;
    }
};

Count sort（计数排序）

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

找出待排序的数组中最大和最小的元素；
统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

计数排序是一个稳定的排序算法。当输入的元素是n 个 0到 k之间的整数时，时间复杂度是O(n+k)，空间复杂度也是O(n+k)，其排序速度快于任何比较排序算法。在实际工作中，当k=O(n)，这时算法的时间复杂度可记为O(n)

当k不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。

在这里插入图片描述

Bucket sort（桶排序）

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

设置一个定量的数组当作空桶；
遍历输入数据，并且把数据一个一个放到对应的桶里去；
对每个不是空的桶进行排序；
从不是空的桶里把排好序的数据拼接起来。

复制代码

1
2
3
4
5
6
7
8
9
10
class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        bucket=collections.defaultdict(int)
        for n in nums:
            bucket[n]+=1
        ans=[]
        for i in range(-50000,50001):
            ans+=[i]*bucket[i]
        return ans

桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

在这里插入图片描述

Radix sort（基数排序）

Bin sort

基本思想：

BinSort想法非常简单，首先创建数组A[MaxValue]；然后将每个数放到相应的位置上（例如17放在下标17的数组位置）；最后遍历数组，即为排序后的结果。

当序列中存在较大值时，BinSort 的排序方法会浪费大量的空间开销。

RadixSort

基本思想： 基数排序是在BinSort的基础上，通过基数的限制来减少空间的开销。

（1）首先确定基数为10，数组的长度也就是10.每个数34都会在这10个数中寻找自己的位置.

（2）不同于BinSort会直接将数34放在数组的下标34处，基数排序是将34分开为3和4，第一轮排序根据最末位放在数组的下标4处，第二轮排序根据倒数第二位放在数组的下标3处，然后遍历数组即可。

Reference

算法导论第三版
排序算法总结
十大经典排序算法

最后

以上就是火星上大树最近收集整理的关于leetcode 排序数组十大排序算法实现的全部内容，更多相关leetcode内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：算法与数据结构
浏览次数：66 次浏览
发布日期：2023-08-27 09:10:19
本文链接：https://www.kaopuke.com/article/k-p-k_14_uzo_14_fx_12__7_gx.html

leetcode 排序数组十大排序算法实现

leetcode912. 排序数组十大排序算法实现

文章目录

912. 排序数组

题目描述

排序算法

分类

算法复杂度

Solution Idea

bubble sort(冒泡排序)

Selection sort(选择排序)

Insertion sort(插入排序)

Shell sort（希尔排序）

Merge sort（归并排序）

Quick sort（快速排序）

Heap sort（堆排序）

Count sort（计数排序）

Bucket sort（桶排序）

Radix sort（基数排序）

Bin sort

RadixSort

Reference

最后

评论列表共有 0 条评论

发表评论取消回复

leetcode 排序数组 十大排序算法实现

leetcode912. 排序数组 十大排序算法实现

文章目录

912. 排序数组

题目描述

排序算法

分类

算法复杂度

Solution Idea

bubble sort(冒泡排序)

Selection sort(选择排序)

Insertion sort(插入排序)

Shell sort（希尔排序）

Merge sort（归并排序）

Quick sort（快速排序）

Heap sort（堆排序）

Count sort（计数排序）

Bucket sort（桶排序）

Radix sort（基数排序）

Bin sort

RadixSort

Reference

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

微信扫一扫：分享

leetcode 排序数组十大排序算法实现

leetcode912. 排序数组十大排序算法实现

发表评论取消回复