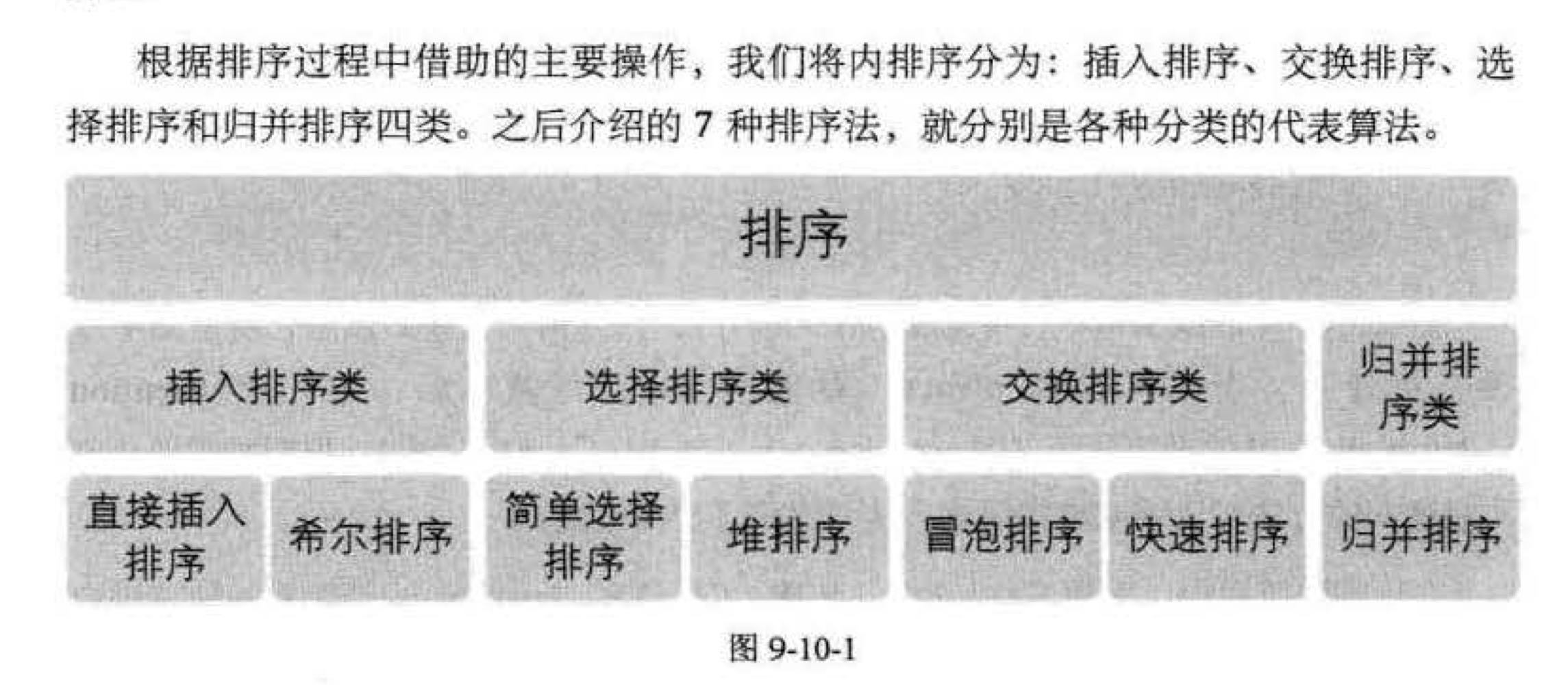
Leetcode刷题——数组排序

算法简介

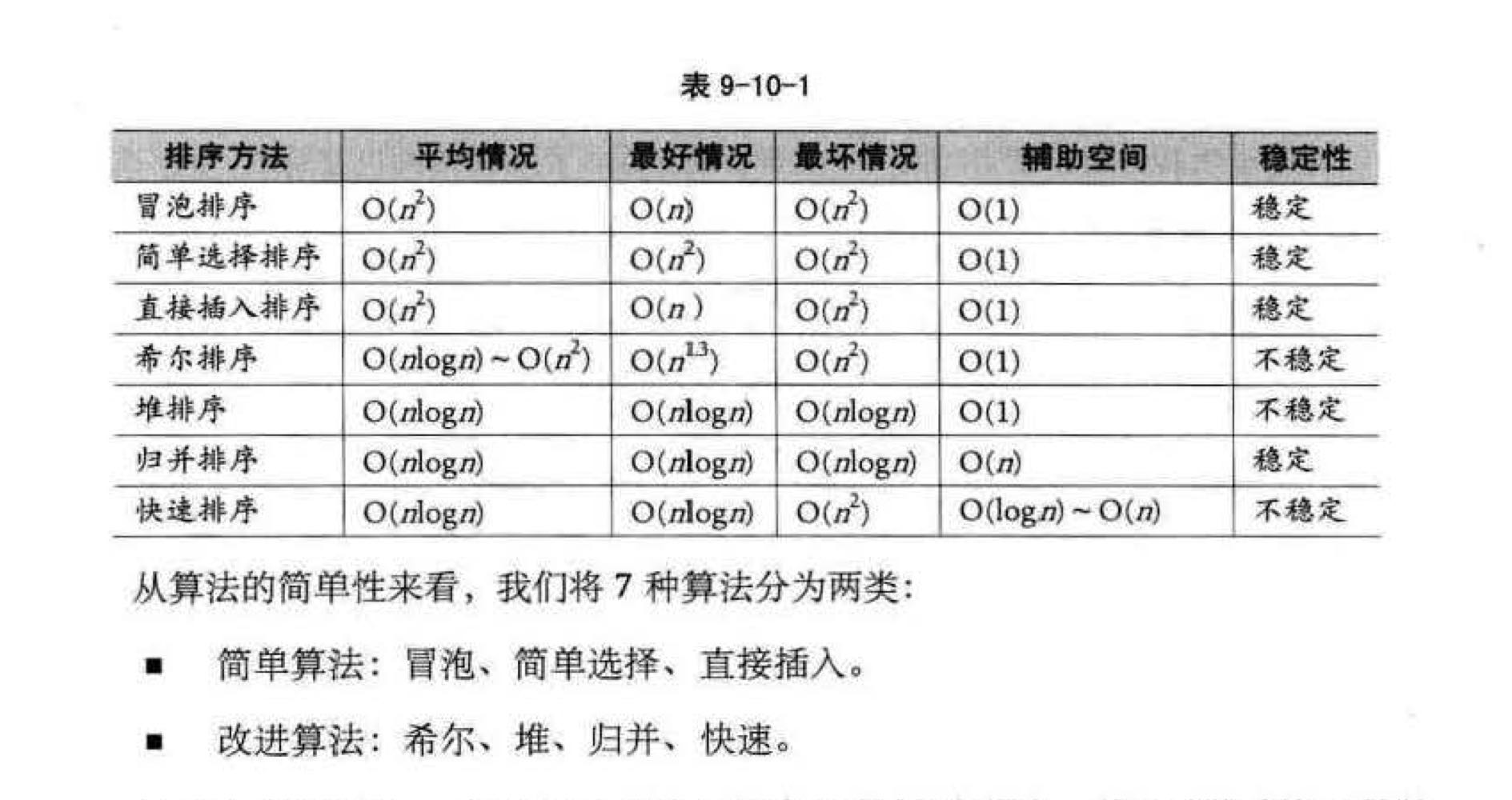
• 排序稳定性
  如果排序前序列中x领先于y，排序后x仍领先于y，则称该排序方法是稳定的；反之为不稳定的。
  
  

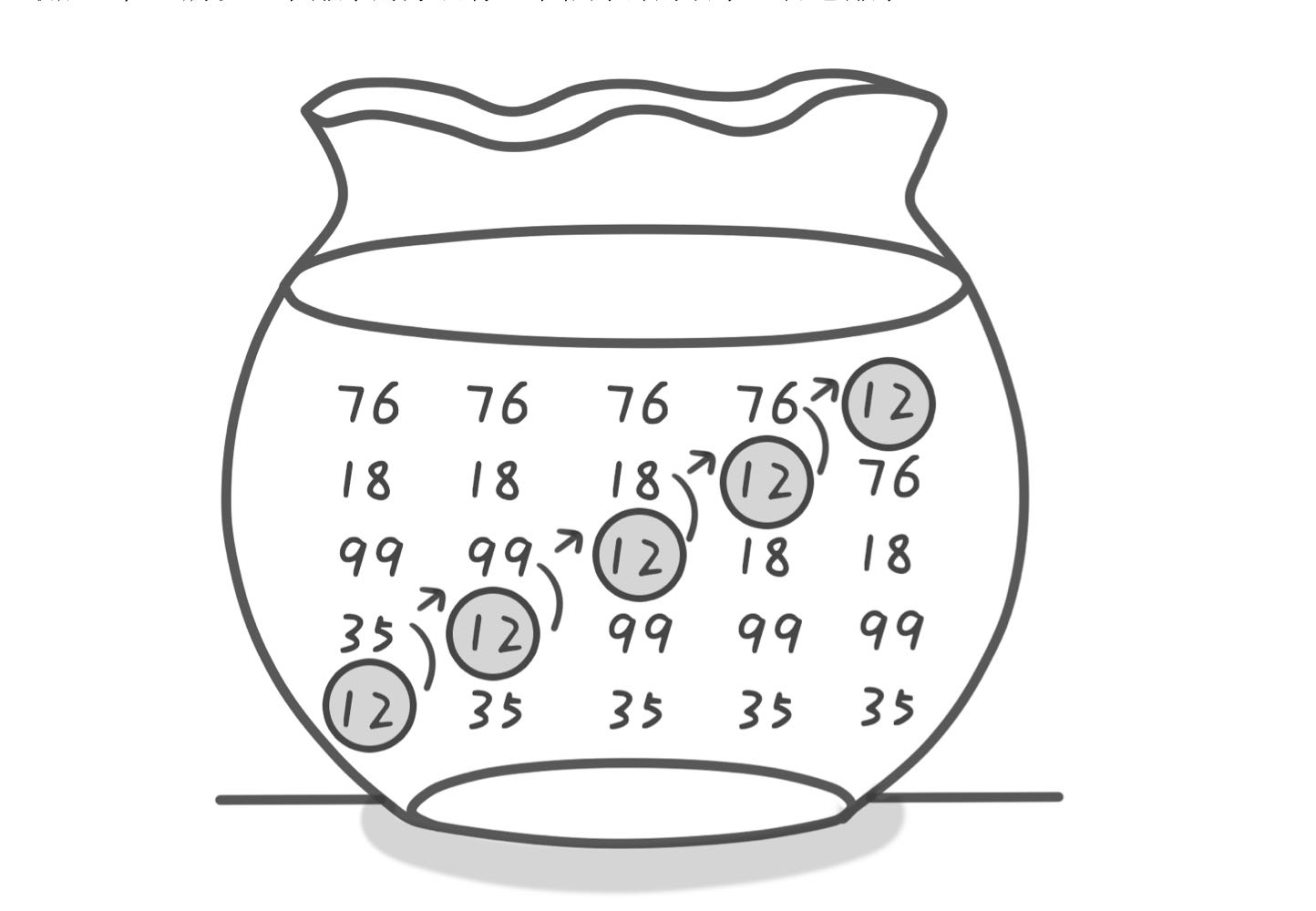
1. 冒泡排序
   是一种交换排序，两两比较相邻记录，如果反序就交换，直到没有反序的记录为止，使得较小的数字如同气泡般上浮。
   

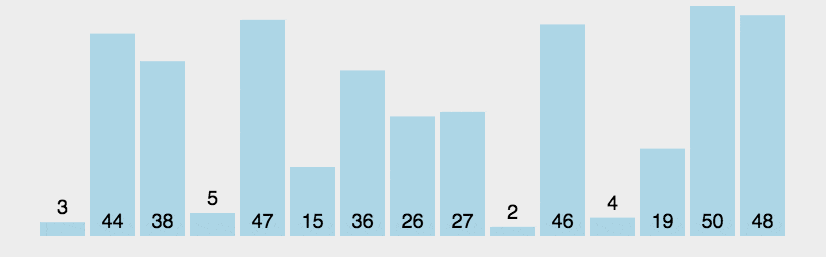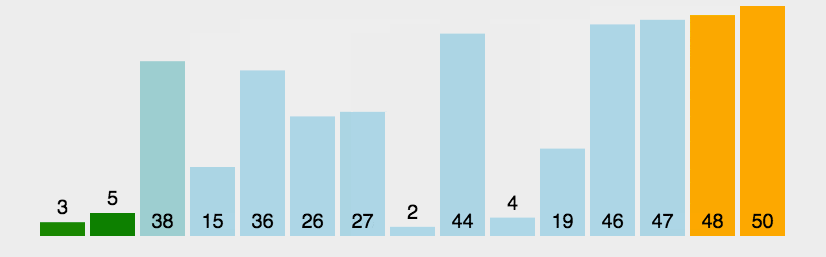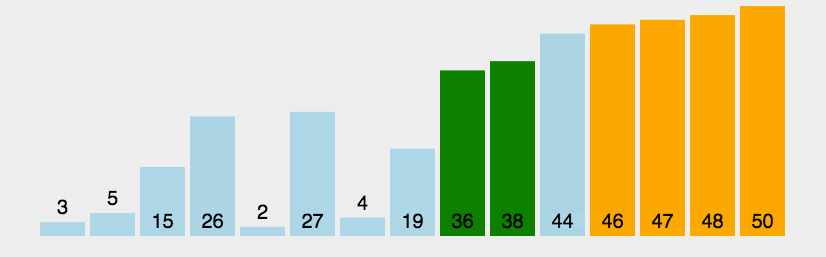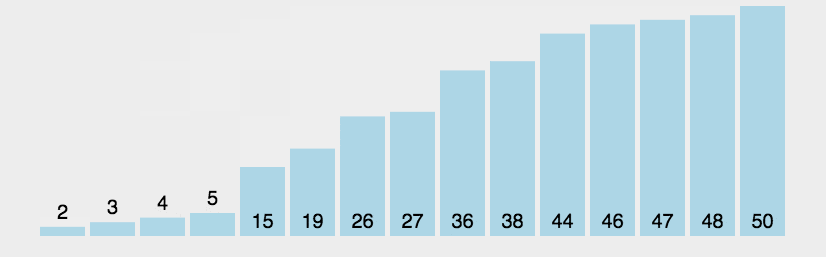
def bubbleSort(arr):
    for i in range(len(arr)):
    	flag = FLASE
        for j in range(len(arr) - i - 1):
            if arr[j] > arr[j + 1]:
            	arr[j], arr[j + 1] = arr[j + 1], arr[j]
            	flag = TRUE
            if not flag:
            	break   
    return arr

• 算法优化
  • 添加标记变量flag
    当没有任何数据交换时，说明序列已有序，增加flag标记，避免无意义的循环判断。
  • 鸡尾酒排序——在特定条件下减少排序回合数，但代码量增加了。

def cocktail_sort(iterable):
    '''鸡尾酒排序（英语：Cocktail Sort/Shaker Sort）是冒泡排序的轻微变形，
    它还有很多奇怪的名字，双向冒泡排序 (Bidirectional Bubble Sort)、
    波浪排序 (Ripple Sort)、摇曳排序 (Shuffle Sort)、
    飞梭排序 (Shuttle Sort) 和欢乐时光排序 (Happy Hour Sort)
    原理：
     1. 对序列向尾部做升序冒泡排序，最大元素沉落尾部。
     2. 对序列向头部做降序冒泡排序，最小元素升到头部。
     3. 交替重复步骤1、2，逐渐缩小无序元素范围，直到没有无序元素。
    时间复杂度：O(n^2)
    稳定性： 稳定
    '''
    for i in range(len(iterable) - 1, 0, -1):
        bubbled = 0

        for j in range(i):
            if iterable[j] > iterable[j + 1]:
                iterable[j], iterable[j + 1] = iterable[j + 1], iterable[j]
                bubbled = 1
        
        for j in range(i, 0, -1):
            if iterable[j] < iterable[j - 1]:
                iterable[j], iterable[j - 1] = iterable[j - 1], iterable[j]
                bubbled = 1

        if not bubbled: break

    return iterable

2. 选择排序
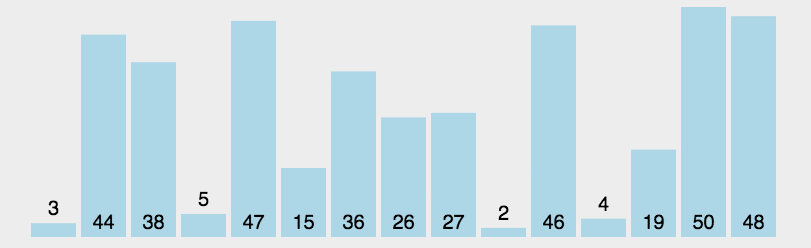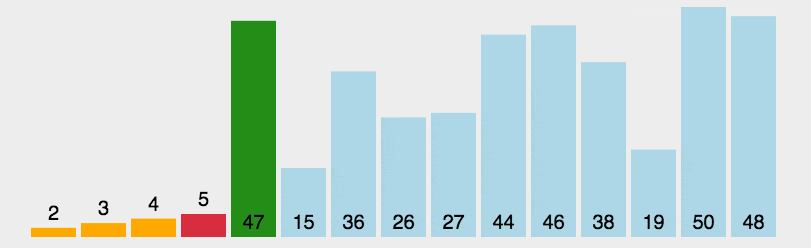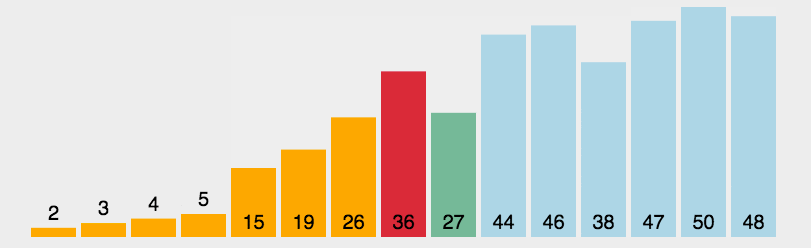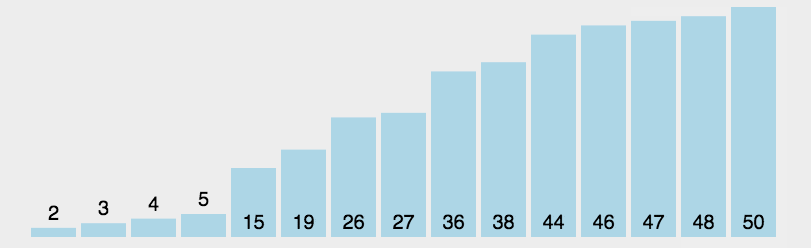
   每一趟排序中，从剩余未排序元素中选择一个最小的元素，与未排好序的元素最前面的那个元素交换位置。
   

def selectionSort(arr):
    for i in range(len(arr) - 1):
        # 记录未排序序列中最小数的索引
        min_i = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_i]:
                min_i = j
        # 如果找到最小数，将 i 位置上元素与最小数位置上元素进行交换
        if i != min_i:
            arr[i], arr[min_i] = arr[min_i], arr[i]
            
    return arr

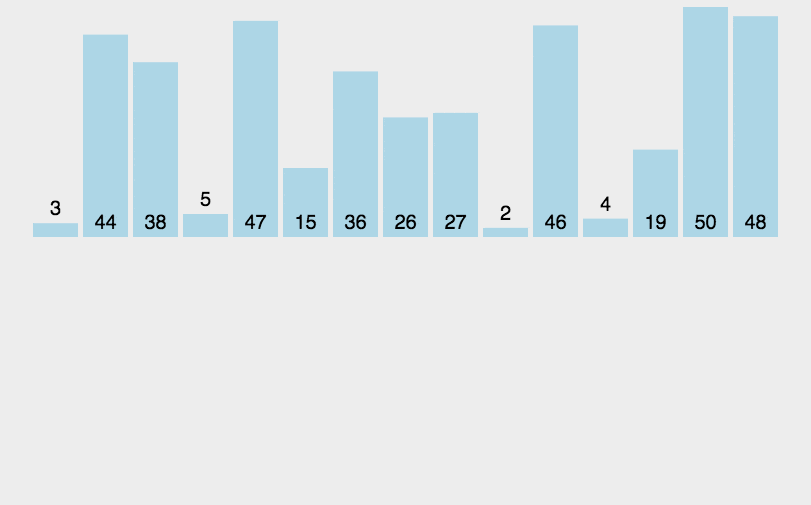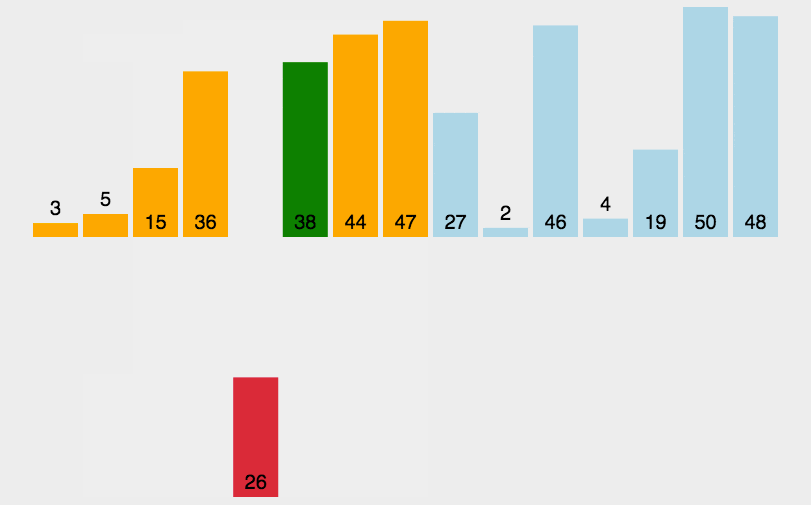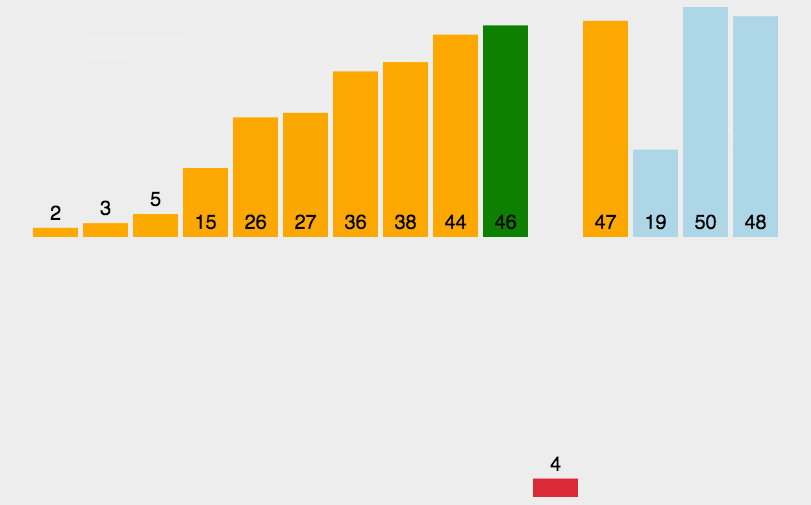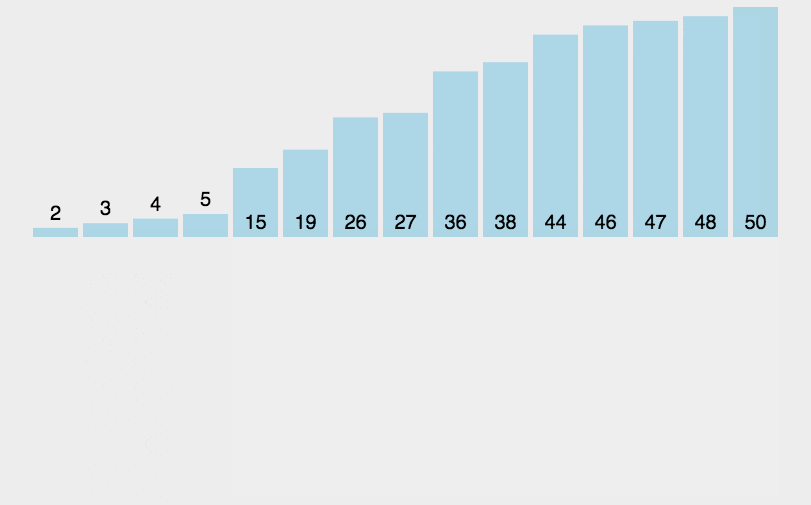
4. 插入排序
   将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录数增1的有序表，需要一个记录的辅助空间。
   

def insertionSort(arr):
    for i in range(1, len(arr)):
        temp = arr[i]
        j = i
        while j > 0 and arr[j - 1] > temp:
            arr[j] = arr[j - 1]
            j -= 1
        arr[j] = temp
        
    return arr

6. 希尔排序
   将整个序列切按照一定的间隔取值划分为若干个子序列，每个子序列分别进行插入排序。然后逐渐缩小间隔进行下一轮划分子序列和插入排序。直至最后一轮排序间隔为 1，对整个序列进行插入排序。
   满足基本有序：小的关键字基本在前面，大的基本在后面，不大不小基本在中间。可以将相距某个“增量”的记录组成一个子序列，这样保证子序列分别进行直接插入排序后得到的结果是基本有序而不是局部有序。
   
   
   

def shellSort(arr):
	size = len(arr)
    gap = size // 2
    
    while gap > 0:
        for i in range(gap, size):
            temp = arr[i]
            j = i
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap = gap // 2
    return arr

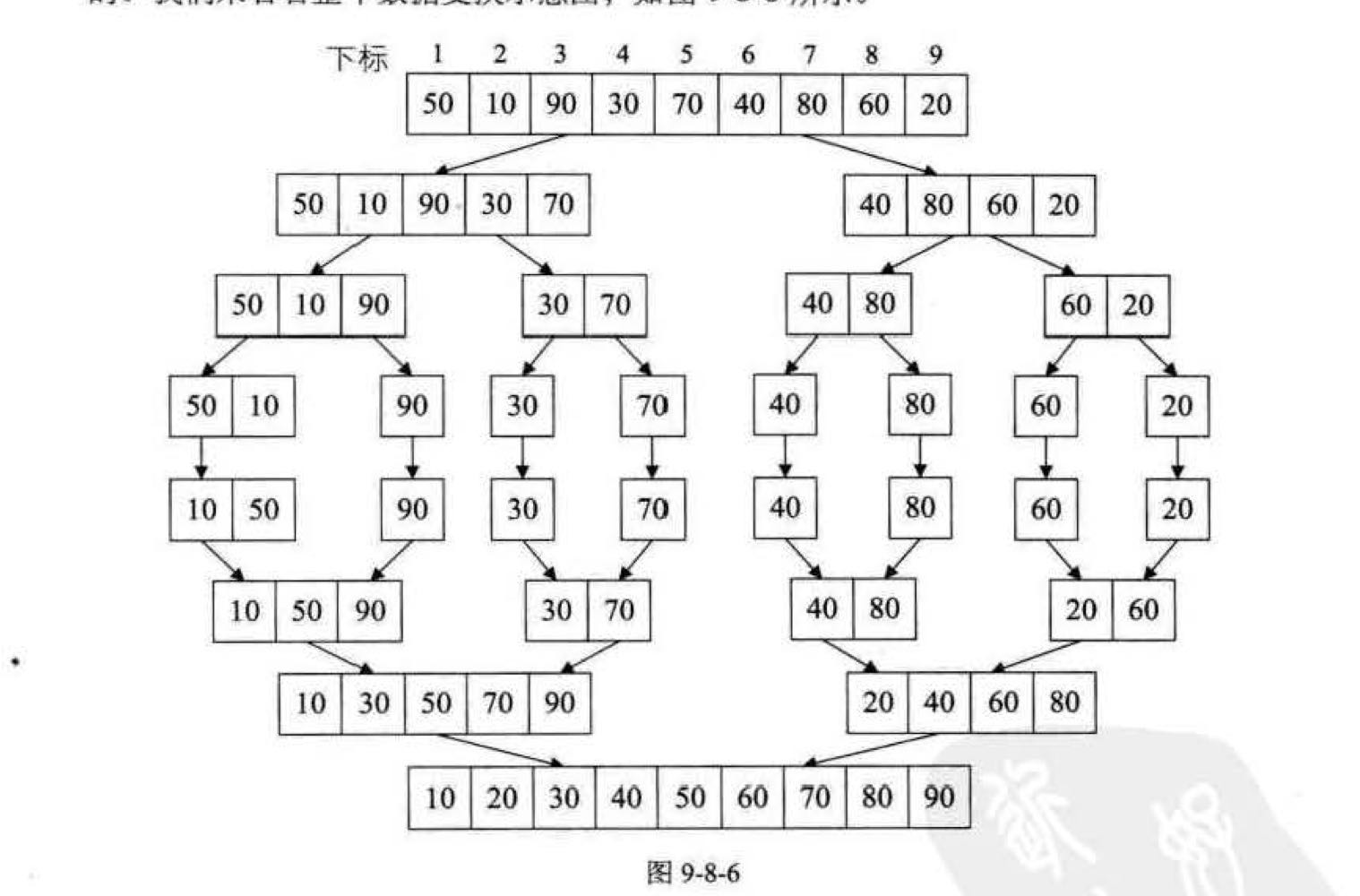
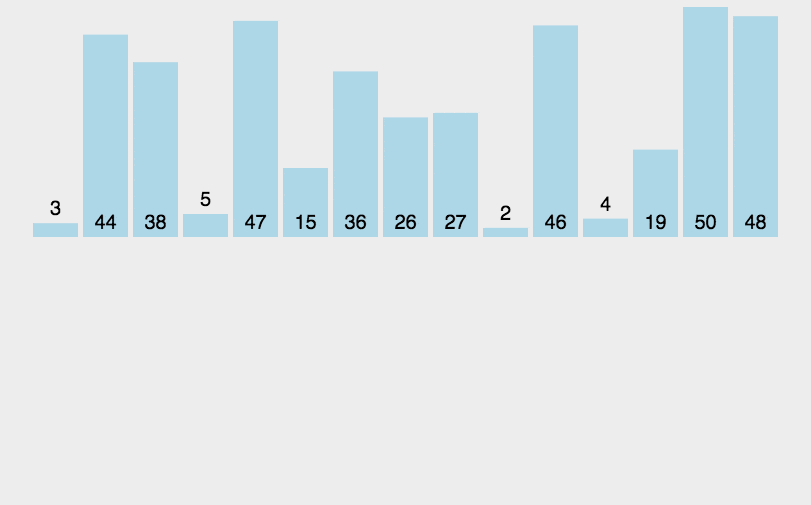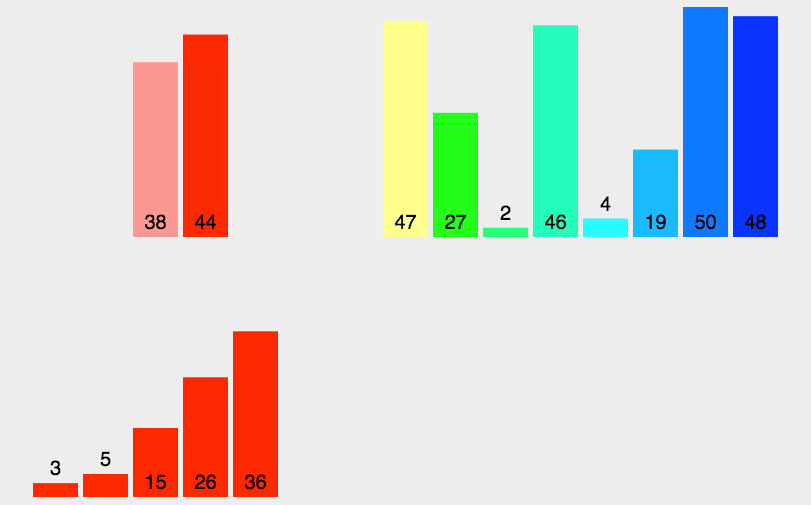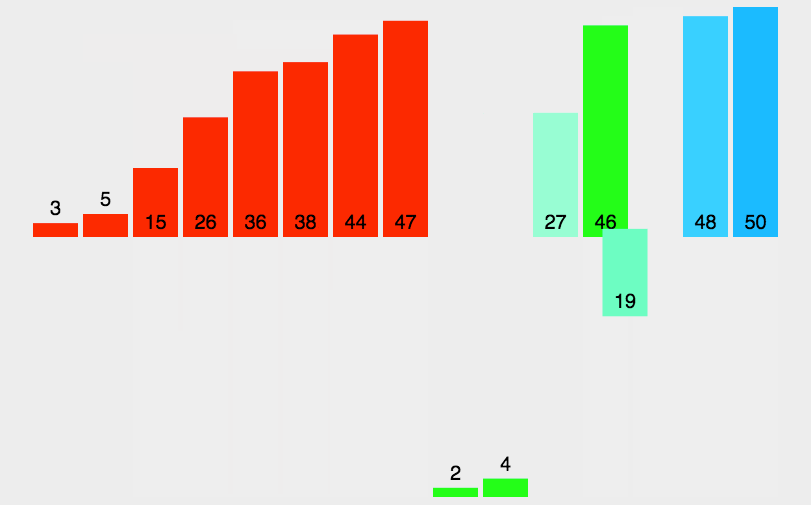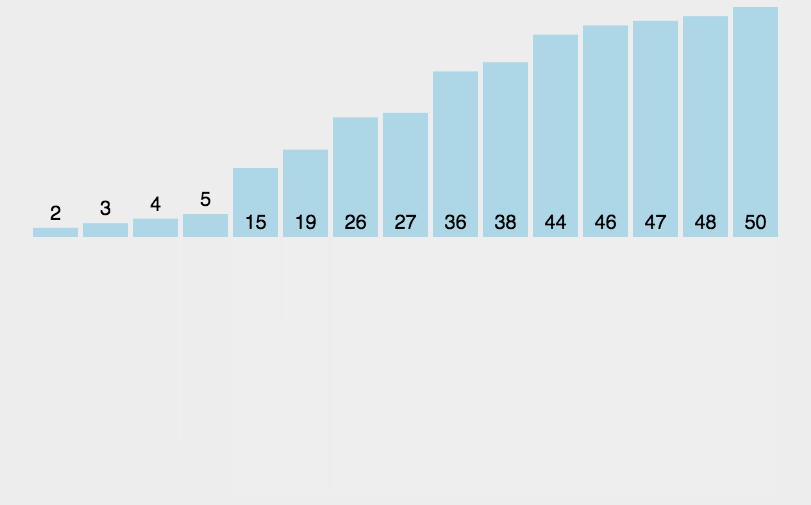
8. 归并排序
   采用经典的分治策略，先递归地将当前序列平均分成两半。然后将有序序列两两合并，最终合并成一个有序序列。
   
   

def merge(left_arr, right_arr):
    arr = []
    while left_arr and right_arr:
        if left_arr[0] <= right_arr[0]:
            arr.append(left_arr.pop(0))
        else:
            arr.append(right_arr.pop(0))
    while left_arr:
        arr.append(left_arr.pop(0))
    while right_arr:
        arr.append(right_arr.pop(0))
    return arr

def mergeSort(arr):
    size = len(arr)
    if size < 2:
        return arr
    mid = len(arr) // 2
    left_arr, right_arr = arr[0: mid], arr[mid:]
    return merge(mergeSort(left_arr), mergeSort(right_arr))

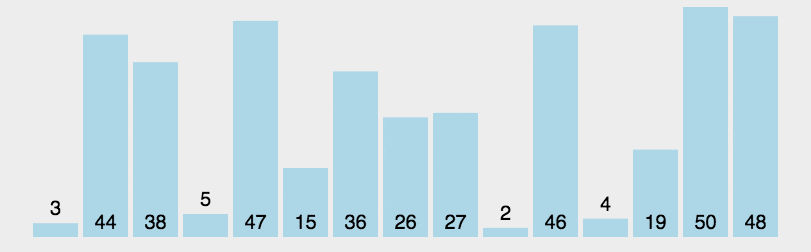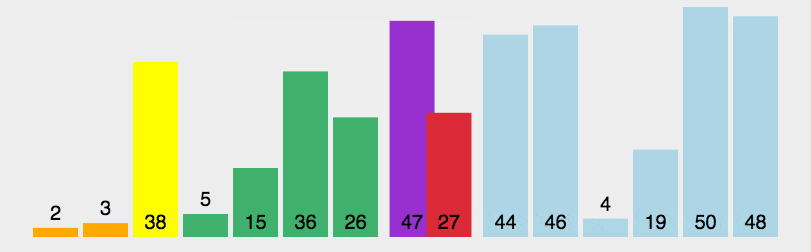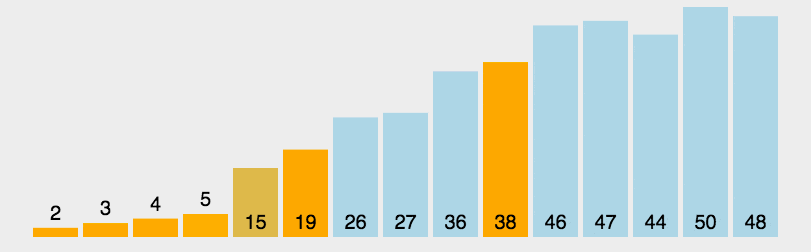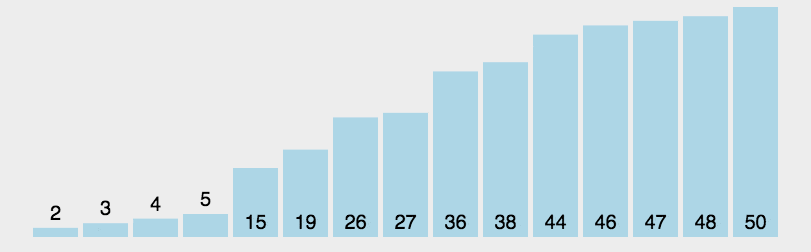
10. 快速排序
    通过一趟排序将无序序列分为独立的两个序列，第一个序列的值均比第二个序列的值小。然后递归地排列两个子序列，以达到整个序列有序。
    

• 优化
  • 优化枢轴选取
  • 优化不必要的交换——采用替换而不是交换的方式进行操作
  • 优化小数组的排序方案——当high-low 不大于7时，就用直接插入排序，综合利用两种优势完成排序
  • 优化递归操作——尾递归优化，采用迭代而不是递归的方式缩减堆栈深度

import random
#随机选取枢纽法优化：pi为low与high之间的随机值；
#还有三数取中、九数取中等方式用于选择pi
def randomPartition(arr: [int], low: int, high: int):
		i = random.randint(low, high)
		arr[i], arr[high] = arr[high], arr[i]
		return partition(arr, low, high)

def partition(arr: [int], low: int, high: int):
	x = arr[high]
	i = low - 1
	for j in range(low, high):
		if arr[j] <= arr[high]:
			i += 1
			arr[i], arr[j] = arr[j], arr[i]
	arr[i + 1], arr[high] = arr[high], arr[i + 1]
	return i + 1

def quickSort(arr, low, high):
	if low < high:
		pi = randomPartition(arr, low, high)
		quickSort(arr, low, pi - 1)
		quickSort(arr, pi + 1, high)

	return arr

12. 堆排序
    借用「堆结构」所设计的排序算法。将数组转化为大顶堆，重复从大顶堆中取出数值最大的节点，并让剩余的堆维持大顶堆性质。大顶堆：根节点值 ≥ 子节点值；小顶堆：根节点值 ≤ 子节点值
    堆具有完全二叉树的性质：
    
    
    
    
    

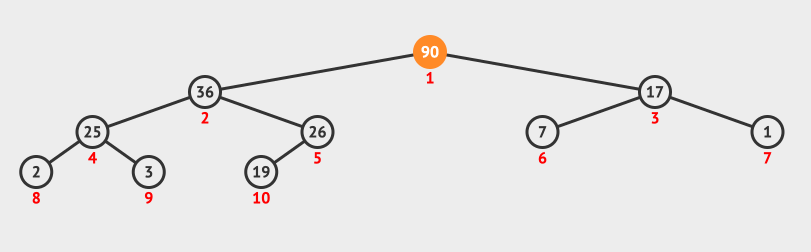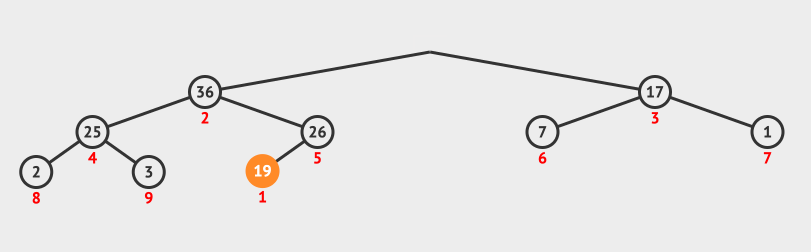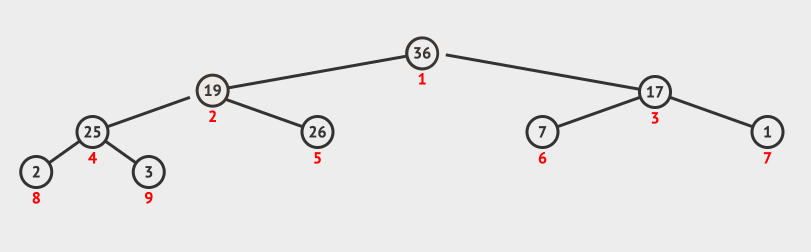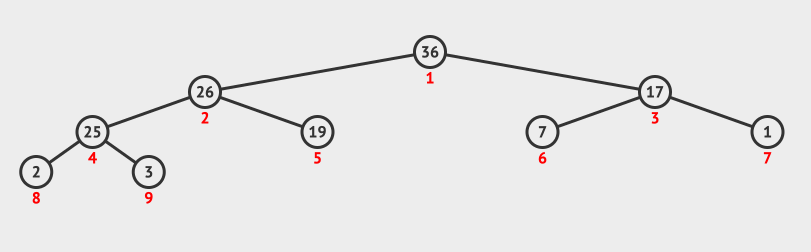
# 调整为大顶堆
def heapify(arr: [int], index: int, end: int):
	left = index * 2 + 1
	right = left + 1
	while left <= end:
		# 当前节点为非叶子结点
		max_index = index
		if arr[left] > arr[max_index]:
			max_index = left
		if right <= end and arr[right] > arr[max_index]:
			max_index = right
		if index == max_index:
			# 如果不用交换，则说明已经交换结束
			break
		arr[index], arr[max_index] = arr[max_index], arr[index]
		# 继续调整子树
		index = max_index
		left = index * 2 + 1
		right = left + 1

# 初始化大顶堆
def buildMaxHeap(arr: [int]):
	size = len(arr)
	# (size-2) // 2 是最后一个非叶节点，叶节点不用调整
	for i in range((size - 2) // 2, -1, -1):
		heapify(arr, i, size - 1)
	return arr

# 升序堆排序，思路如下：
# 1. 先建立大顶堆
# 2. 让堆顶最大元素与最后一个交换，然后调整第一个元素到倒数第二个元素，这一步获取最大值
# 3. 再交换堆顶元素与倒数第二个元素，然后调整第一个元素到倒数第三个元素，这一步获取第二大值
# 4. 以此类推，直到最后一个元素交换之后完毕。
def maxHeapSort(arr: [int]):
	buildMaxHeap(arr)
	size = len(arr)
	for i in range(size):
		arr[0], arr[size-i-1] = arr[size-i-1], arr[0]
		heapify(arr, 0, size-i-2)
	return arr

14. 计数排序
    使用一个额外的数组 counts，其中第 i 个元素 counts[i] 是待排序数组 arr 中值等于 i 的元素个数。然后根据数组 counts 来将 arr 中的元素排到正确的位置。
    当最大值和最小值差距过大时，并不适合用计数排序。当数列元素不是整数时，也不适合用计数排序，上述问题可以通过桶排序来解决，借助桶的区间范围加以统计。
    

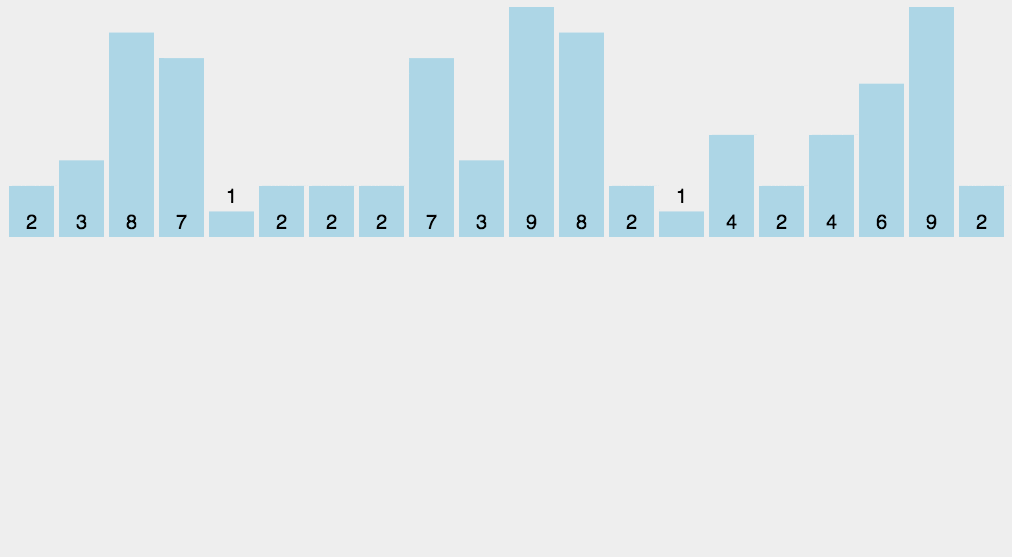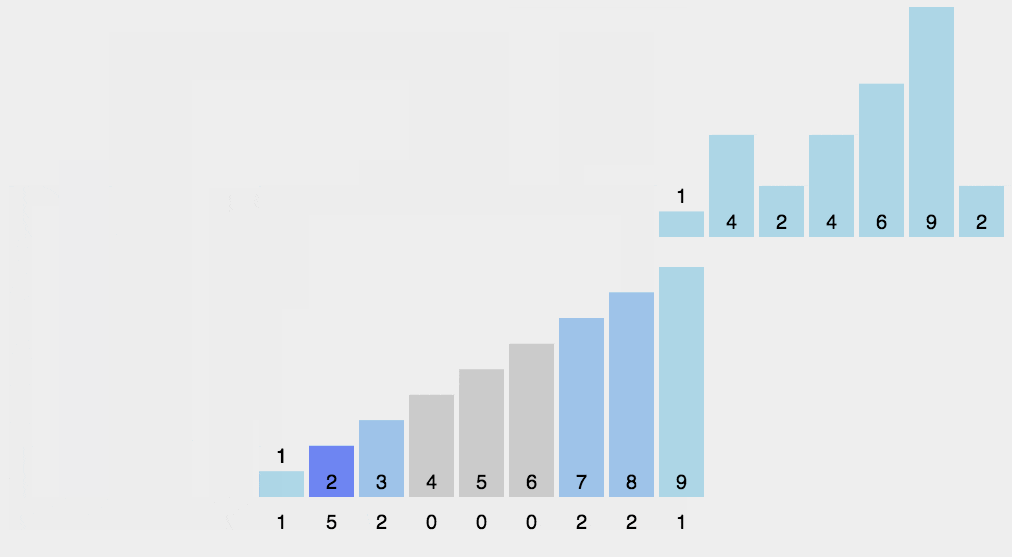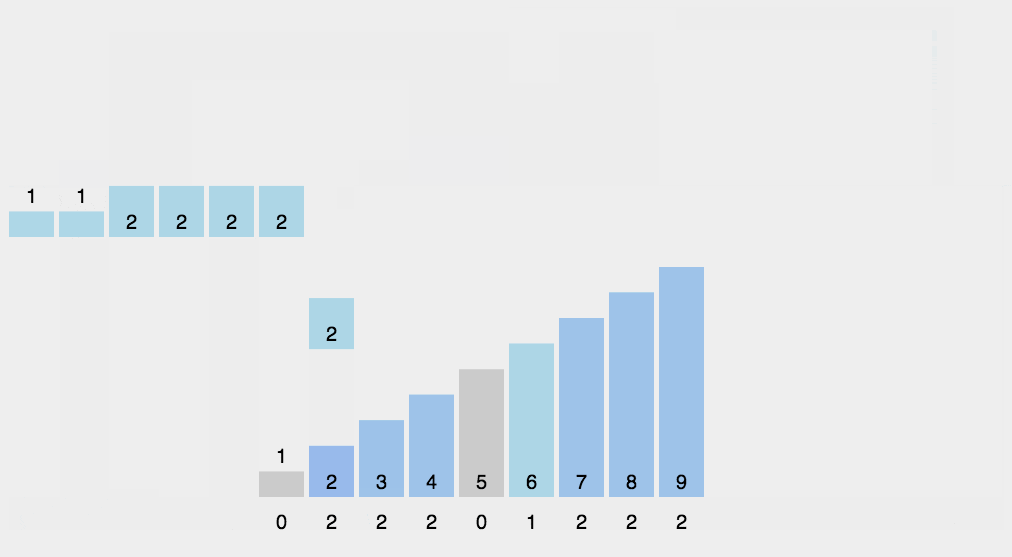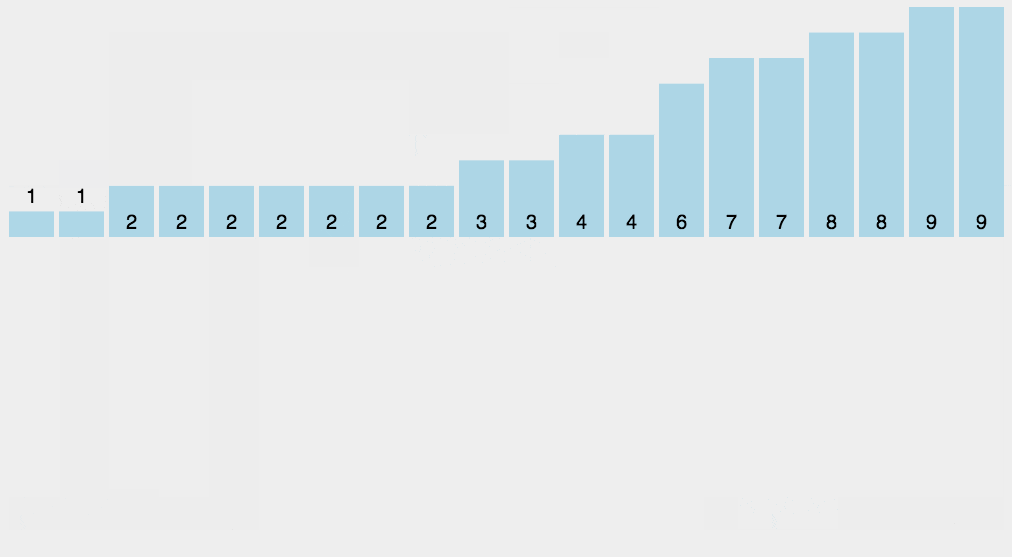
def countingSort(arr):
    arr_min, arr_max = min(arr), max(arr)
    size = arr_max - arr_min + 1
    counts = [0 for _ in range(size)]
    
    for num in arr:
    	#用数列最小值作为偏移量，计算下标出现次数
        counts[num - arr_min] += 1
    for j in range(1, size):
        counts[j] += counts[j - 1]
    
    res = [0 for _ in range(len(arr))]
    for i in range(len(arr) - 1, -1, -1):
        res[counts[arr[i] - arr_min] - 1] = arr[i]
        counts[arr[i] - arr_min] -= 1
    
    return res  

• 优化
  • 最小值作为偏移量，计算整数在统计数组下标的出现次数
  • 保存原数组位置信息，保持稳定性

16. 桶排序
    将未排序的数组分到若干个「桶」中，每个桶的元素再进行单独排序。——稳定排序
    

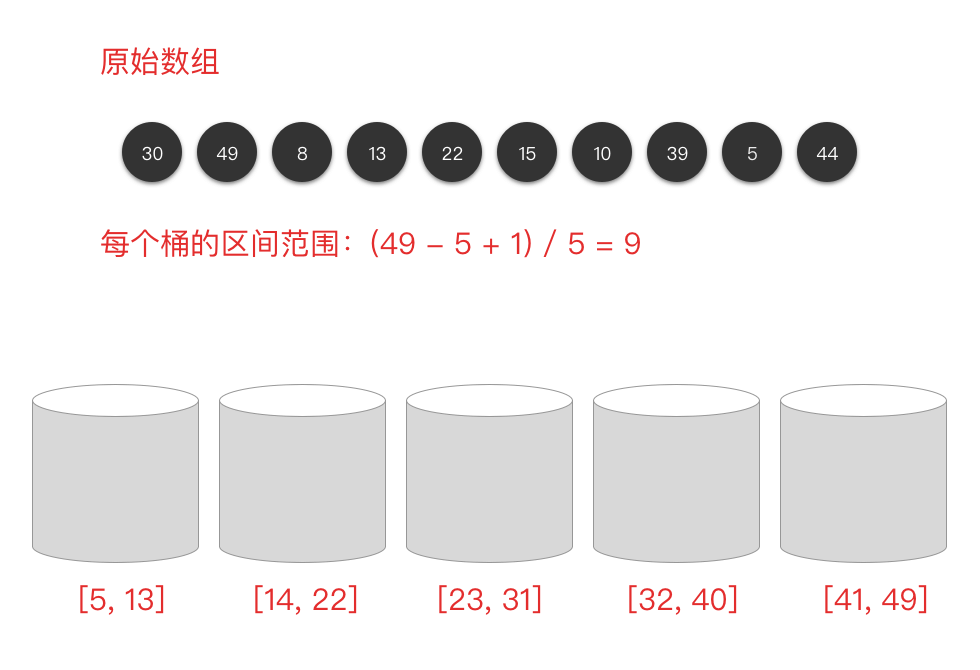
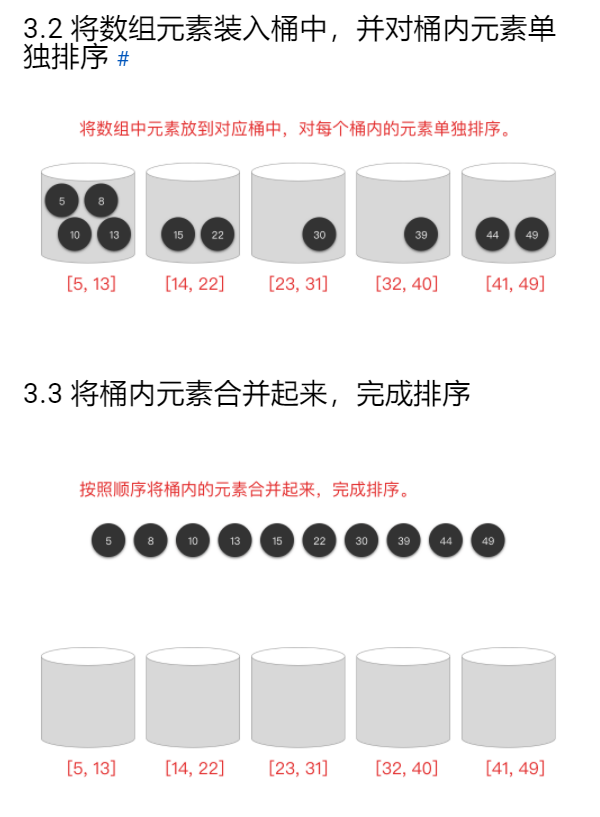
def insertionSort(arr):
    for i in range(1, len(arr)):
        temp = arr[i]
        j = i
        while j > 0 and arr[j - 1] > temp:
            arr[j] = arr[j - 1]
            j -= 1
        arr[j] = temp
        
    return arr
    
    
def bucketSort(arr, bucket_size = 5):
    arr_min, arr_max = min(arr), max(arr)
    bucket_count = (arr_max - arr_min) // bucket_size + 1
    buckets = [[] for _ in range(bucket_count)]
    
    for num in arr:
        buckets[(num - arr_min) // bucket_size].append(num)
        
    res = []
    for bucket in buckets:
        insertionSort(bucket)
        res.extend(bucket)
    
    return res  

18. 基数排序
    将整数按位数切割成不同的数字，然后按每个位数分别比较进行排序。——稳定排序
    

def radixSort(arr):
    size = len(str(max(arr)))
    
    for i in range(size):
        buckets = [[] for _ in range(10)]
        for num in arr:
            buckets[num // (10**i) % 10].append(num)
    	arr.clear()
    	for bucket in buckets:
        	for num in bucket:
                arr.append(num)
            
    return arr

刷题实战

• 0283 移动零

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        left = 0
        right = 0
        while right < len(nums):
            if nums[right] != 0:
                nums[left], nums[right] = nums[right], nums[left]
                left += 1
            right += 1

• 0506 相对名次
• sorted函数

class Solution:
    def findRelativeRanks(self, score: List[int]) -> List[str]:
        medals = ["Gold Medal", "Silver Medal", "Bronze Medal"]
        awards = medals + [str(i+1) for i in range(3,len(score))]
        score_to_award = {s:a for s,a in zip(sorted(score,reverse=True),awards)}
        res = [score_to_award[s] for s in score]
        return res

• 自定义排序函数

class Solution:
	# 希尔排序
    def shellSort(self, arr):
        size = len(arr)
        gap = size // 2
        while gap > 0:
            for i in range(gap, size):
                temp = arr[i]
                j = i
                while j >= gap and arr[j - gap] < temp:
                    arr[j] = arr[j - gap]
                    j -= gap
                arr[j] = temp
            gap = gap // 2
        return arr

    def findRelativeRanks(self, score: List[int]) -> List[str]:
    	#浅复制，保留原数组数据
        nums = score.copy()
        nums = self.shellSort(nums)
        #创建字典保留数值及排序
        score_map = dict()
        for i in range(len(nums)):
            score_map[nums[i]] = i + 1

        res = []
        #重新赋值
        for i in range(len(score)):
            if score[i] == nums[0]:
                res.append("Gold Medal")
            elif score[i] == nums[1]:
                res.append("Silver Medal")
            elif score[i] == nums[2]:
                res.append("Bronze Medal")
            else:
            #否则保留数值排序标号
                res.append(str(score_map[score[i]]))
        return res

• 面试题10.01 合并排序的数组

class Solution:
    def merge(self, A: List[int], m: int, B: List[int], n: int) -> None:
        """
        Do not return anything, modify A in-place instead.
        """
        arr = []
        #双指针排序
        index_A, index_B = 0, 0
        while index_A < m and index_B < n:
            if A[index_A] <= B[index_B]:
                arr.append(A[index_A])
                index_A += 1
            else:
                arr.append(B[index_B])
                index_B += 1
        while index_A < m:
            arr.append(A[index_A])
            index_A += 1
        while index_B < n:
            arr.append(B[index_B])
            index_B += 1
        for i in range(m + n):
            A[i] = arr[i]

• 0088 合并两个有序数组

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        p1 = m - 1
        p2 = n - 1
        p = m + n - 1
        while p1 >= 0 and p2 >= 0:
            if nums1[p1] < nums2[p2]:
                nums1[p] = nums2[p2]
                p2 -= 1
            else:
                nums1[p] = nums1[p1]
                p1 -= 1
            p -= 1

        nums1[:p2+1] = nums2[:p2+1]

• 0169 多数元素

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        numDict = dict()
        for num in nums:
            if num in numDict:
                numDict[num] += 1
            else:
                numDict[num] = 1
        max = 0
        max_index = -1
        for num in numDict:
            if numDict[num] > max:
                max = numDict[num]
                max_index = num
        return max_index

• 剑指offer 40 最小的k个数

class Solution:
    def heapify(self, nums: [int], index: int, end: int):
        left = index * 2 + 1
        right = left + 1
        while left <= end:
            # 当前节点为非叶子节点
            max_index = index
            if nums[left] > nums[max_index]:
                max_index = left
            if right <= end and nums[right] > nums[max_index]:
                max_index = right
            if index == max_index:
                # 如果不用交换，则说明已经交换结束
                break
            nums[index], nums[max_index] = nums[max_index], nums[index]
            # 继续调整子树
            index = max_index
            left = index * 2 + 1
            right = left + 1

    # 初始化大顶堆
    def buildMaxHeap(self, nums: [int], k: int):
        # (k-2) // 2 是最后一个非叶节点，叶节点不用调整
        for i in range((k - 2) // 2, -1, -1):
            self.heapify(nums, i, k - 1)
        return nums

    def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
        size = len(arr)
        if k <= 0 or not arr:
            return []
        if size <= k:
            return arr

        self.buildMaxHeap(arr, k)
        for i in range(k, size):
            if arr[i] < arr[0]:
                arr[i], arr[0] = arr[0], arr[i]
                self.heapify(arr, 0, k - 1)

        return arr[:k]

• 1122 数组的相对排序

class Solution:
    def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
        count = [0 for _ in range(1010)]
        for num1 in arr1:
            count[num1] += 1
        res = []
        for num2 in arr2:
            while count[num2] > 0:
                res.append(num2)
                count[num2] -= 1

        for num in range(len(count)):
            while count[num] > 0:
                res.append(num)
                count[num] -= 1

        return res

• 0561 数组拆分I

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        nums.sort()
        return sum(nums[::2])

• 0217 存在重复元素

class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        numDict = dict()
        for i in range(len(nums)):
            num = nums[i]
            if num in numDict:
                return True
            else:
                numDict[num] = num
        return False

• 0136 只出现一次的数字

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        if len(nums) == 1:
            return nums[0]
        ans = 0
        for i in range(len(nums)):
            ans ^= nums[i]
        return ans

• 0056 合并区间

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        intervals.sort(key=lambda x: x[0])

        ans = []
        for interval in intervals:
            if not ans or ans[-1][1] < interval[0]:
                ans.append(interval)
            else:
                ans[-1][1] = max(ans[-1][1], interval[1])
        return ans

• 剑指Offer 45 把数组排成最小的数

import functools

class Solution:
    def minNumber(self, nums: List[int]) -> str:
        def cmp(a, b):
            if a + b == b + a:
                return 0
            elif a + b > b + a:
                return 1
            else:
                return -1

        nums_s = list(map(str, nums))
        nums_s.sort(key=functools.cmp_to_key(cmp))
        return ''.join(nums_s)

• 数组中的第k个最大元素

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        # 调整为大顶堆
        def heapify(nums, index, end):
            left = index * 2 + 1
            right = left + 1
            while left <= end:
                # 当前节点为非叶子节点
                max_index = index
                if nums[left] > nums[max_index]:
                    max_index = left
                if right <= end and nums[right] > nums[max_index]:
                    max_index = right
                if index == max_index:
                    # 如果不用交换，则说明已经交换结束
                    break
                nums[index], nums[max_index] = nums[max_index], nums[index]
                # 继续调整子树
                index = max_index
                left = index * 2 + 1
                right = left + 1
                
        # 初始化大顶堆
        def buildMaxHeap(nums):
            size = len(nums)
            # (size-2) // 2 是最后一个非叶节点，叶节点不用调整
            for i in range((size - 2) // 2, -1, -1):
                heapify(nums, i, size - 1)
            return nums

        buildMaxHeap(nums)
        size = len(nums)
        for i in range(k-1):
            nums[0], nums[size-i-1] = nums[size-i-1], nums[0]
            heapify(nums, 0, size-i-2)
        return nums[0]

• 0075 颜色分类

class Solution:
    def sortColors(self, nums: List[int]) -> None:
        left = 0
        right = len(nums) - 1
        index = 0
        while index <= right:
            if index < left:
                index += 1
            elif nums[index] == 0:
                nums[index], nums[left] = nums[left], nums[index]
                left += 1
            elif nums[index] == 2:
                nums[index], nums[right] = nums[right], nums[index]
                right -= 1
            else:
                index += 1

• 0912 排序数组（多种解法）

class Solution:
    def insertionSort(self, arr):
        for i in range(1, len(arr)):
            temp = arr[i]
            j = i
            while j > 0 and arr[j - 1] > temp:
                arr[j] = arr[j - 1]
                j -= 1
            arr[j] = temp
            
        return arr
    
    def sortArray(self, nums: List[int]) -> List[int]:
        return self.insertionSort(nums)

• 0215 数组中第K个最大元素

import random
class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        def randomPartition(nums, low, high):
            i = random.randint(low, high)
            nums[i], nums[high] = nums[high], nums[i]
            return partition(nums, low, high)

        def partition(nums, low, high):
            x = nums[high]
            i = low-1
            for j in range(low, high):
                if nums[j] <= nums[high]:
                    i += 1
                    nums[i], nums[j] = nums[j], nums[i]
            nums[i+1], nums[high] = nums[high], nums[i+1]
            return i+1

        def quickSort(nums, low, high, k):
            n = len(nums)
            if low < high:
                pi = randomPartition(nums, low, high)
                if pi == n-k:
                    return nums[len(nums)-k]
                if pi > n-k:
                    quickSort(nums, low, pi-1, k)
                if pi < n-k:
                    quickSort(nums, pi+1, high, k)

            return nums[len(nums)-k]

        return quickSort(nums, 0, len(nums)-1, k)

• 剑指Offer 51 数组中的逆序对

import bisect

class BinaryIndexTree:

    def __init__(self, n):
        self.size = n
        self.tree = [0 for _ in range(n + 1)]

    def lowbit(self, index):
        return index & (-index)

    def update(self, index, delta):
        while index <= self.size:
            self.tree[index] += delta
            index += self.lowbit(index)

    def query(self, index):
        res = 0
        while index > 0:
            res += self.tree[index]
            index -= self.lowbit(index)
        return res

class Solution:
    def reversePairs(self, nums: List[int]) -> int:
        size = len(nums)
        sort_nums = sorted(nums)
        for i in range(size):
            nums[i] = bisect.bisect_left(sort_nums, nums[i]) + 1

        bit = BinaryIndexTree(size)
        ans = 0
        for i in range(size):
            bit.update(nums[i], 1)
            ans += (i + 1 - bit.query(nums[i]))
        return ans

• 0315 计算右侧小于当前元素的个数-困难

import bisect

class BinaryIndexTree:

    def __init__(self, n):
        self.size = n
        self.tree = [0 for _ in range(n + 1)]

    def lowbit(self, index):
        return index & (-index)

    def update(self, index, delta):
        while index <= self.size:
            self.tree[index] += delta
            index += self.lowbit(index)

    def query(self, index):
        res = 0
        while index > 0:
            res += self.tree[index]
            index -= self.lowbit(index)
        return res

class Solution:
    def countSmaller(self, nums: List[int]) -> List[int]:
        size = len(nums)
        if size == 0:
            return []
        if size == 1:
            return [0]

        # 离散化
        sort_nums = list(set(nums))
        sort_nums.sort()
        size_s = len(sort_nums)
        bit = BinaryIndexTree(size_s)

        ans = [0 for _ in range(size)]
        for i in range(size - 1, -1, -1):
            index = bisect.bisect_left(sort_nums, nums[i]) + 1
            ans[i] = bit.query(index - 1)
            bit.update(index, 1)

        return ans

• 0164 最大间距-困难

class Solution:
    def radixSort(self, arr):
        size = len(str(max(arr)))

        for i in range(size):
            buckets = [[] for _ in range(10)]
            for num in arr:
                buckets[num // (10 ** i) % 10].append(num)
            arr.clear()
            for bucket in buckets:
                for num in bucket:
                    arr.append(num)

        return arr

    def maximumGap(self, nums: List[int]) -> int:
        if len(nums) < 2:
            return 0
        arr = self.radixSort(nums)
        return max(arr[i] - arr[i-1] for i in range(1, len(arr)))

参考资料：
算法通关手册 https://github.com/itcharge/LeetCode-Py
程杰. 大话数据结构 = Play with data structure. 北京: 清华大学出版社, 2011.
啊哈磊. 啊哈! 算法 = Aha! algorithms. 北京: 人民邮电出版社, 2014.
魏梦舒. 漫画算法：小灰的算法之旅 Python篇. 北京：电子工业出版社, 2019.

最后

以上就是强健花瓣为你收集整理的Leetcode刷题——数组排序的全部内容，希望文章能够帮你解决Leetcode刷题——数组排序所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。