计算数字 1 的个数（小于等于 n 的非负整数中数字 1 出现的个数）

448 阅读 0 评论 296 点赞

我是靠谱客的博主自信裙子，这篇文章主要介绍计算数字 1 的个数（小于等于 n 的非负整数中数字 1 出现的个数），现在分享给大家，希望可以做个参考。

写在前面

觉得写得好，有所收获，记得点个关注和点个赞，不胜感激。
这个问题乍一看，我最开始以为是计算二进制位的1的个数（最近对二进制比较敏感，想啥问题都是先想着能不能二进制解决）。然后仔细看了问题之后才发现，其实就是计算十进制中1的个数。其实理解问题之后，感觉也不是很难，一个暴力计算就搞定，不过，光用暴力解决问题并不是我的风格，所以还要想着其他更有效的方式。这里记录这个问题，不是因为他有多难，而是这个问题其实是一个纯粹的数学问题，我们需要进行数学分析就可以很简单的实现出来并解决，而不是使用语言上的奇淫巧技。

描述问题

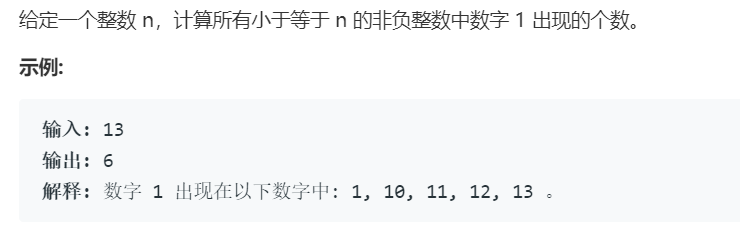
在这里插入图片描述
如果没有事先遇到过，并解决这问题，我相信很多人在第一次遇见这个问题的时候，很容易卡壳。

直接暴力

在算法中，也有所谓的暴力美学，这种思路体现了人最直观的看问题以及解决问题的思路。所以在我们进行其他思路的讲解的时候，还是需要先来看看暴力解决的思路，上下才能有个比较。

我们只要从 $1$ 遍历到 $n$ ，遍历过程中的数，我们用 $i$ 来表示
将 $i$ 转成字符串，数字符串中 $1$ 的个数
将每个字符串里 $1$ 的个数累加到变量 count
返回 count

暴力就是这么简单直观，当然，你可以不转成字符串，直接通过对十取模相除也可以。代码如下：

public int countDigitOne(int n) {
    int num = 0;
    for (int i = 1; i <= n; i++) {
        int temp = i;
        while (temp > 0) {
            if (temp % 10 == 1) {
                num++;
            }
            temp /= 10;
        }
    }
    return num;
}

数学分析

其实吧，上面暴力的思路中，如果我们使用的是取模相除的话，我们就已经接近了数学分析的思路了。不过就是因为没有进一步的深入分析，所以与数学分析正解无缘。数学分析的思路也就是分类，先求所有数中个位是 $1$ 的个数，再求十位是 $1 $ 的个数，再求百位是 $1$ 的个数，以此类推，一直到数的最高位。

这里我们假设我们要计算的数 n 的值为xyzdabc，这个时候，我们计算整个数 n 中，d 位上数字 1 出现的个数。那么此时有三种情况，如下：

当 d == 0 时，那么在 d 位上数字 1 出现的个数为 xyz * 1000
当 d == 1 时，那么在 d 位上数字 1 出现的个数为 xyz * 1000 + abc + 1
当 d > 1 时，那么在 d 位上数字 1 出现的个数为 (xyz + 1) * 1000

其实这个不难理解，当我们考虑千位是 1 的时候，我们将千位定为 1，也就是 xyz1abc。对于 xyz 的话，可以取 0,1,2...(xyz-1)，也就是 xyz 种可能。而 abc 可以取 0,1,2...999，也就是 1000 种可能。这样的话，总共就是 xyz * 1000 种可能。注意到，我们前三位只取到了 xyz - 1，那么如果取 xyz 呢？

此时就出现了上边的三种情况，取决于 d 的值。d == 1 的时候，千位刚好是 1，此时 abc 可以取的值就是 0 到 abc ，所以多加了 abc + 1。d > 1 的时候，d 如果取 1，那么 abc 就可以取 0 到 999，此时就多加了 1000。还不懂？再看一个具体的例子。

如果n = 4560234
让我们统计一下千位有多少个 1
xyz 可以取 0 到 455, abc 可以取 0 到 999
4551000 to 4551999 (1000)
4541000 to 4541999 (1000)
4531000 to 4531999 (1000)
...
  21000 to   21999 (1000)
  11000 to   11999 (1000)    
   1000 to    1999 (1000)
总共就是 456 * 1000

如果 n = 4561234
xyz 可以取 0 到 455, abc 可以取 0 到 999
4551000 to 4551999 (1000)
4541000 to 4541999 (1000)
4531000 to 4531999 (1000)
...
1000 to 1999 (1000)
xyz 还可以取 456, abc 可以取 0 到 234
4561000 to 4561234 (234 + 1)
总共就是 456 * 1000 + 234 + 1

如果 n = 4563234
xyz 可以取 0 到 455, abc 可以取 0 到 999    
4551000 to 4551999 (1000)
4541000 to 4541999 (1000)
4531000 to 4531999 (1000)
...
1000 to 1999 (1000)
xyz 还可以取 456, abc 可以取 0 到 999
4561000 to 4561999 (1000)
总共就是 456 * 1000 + 1000

至于其它位的话是一样的道理。代码的话就很好写了。

public int countDigitOne(int n) {
    int count = 0;
    for (int i = 1; i <= n; i *= 10) {
        int abc = n % i;
        int xyzd = n / i;
        int d = xyzd % 10;
        int xyz = xyzd / 10;
        count += xyz * i;
        if (d == 1) count += abc + 1;
        if (d > 1) count += i;

        //如果不加这句的话，虽然 i 一直乘以 10，但由于溢出的问题
        //i 本来要大于 n 的时候，却小于了 n 会再次进入循环
        //此时代表最高位是 1 的情况也考虑完成了
        if (xyz == 0) break;
    }
    return count;
}

然后代码的话，可以再简化一下，注意到 d > 1 的时候，我们多加了一个 i。我们可以通过计算 long xyz = xyzd / 10; 的时候，给 xyzd 多加 8，从而使得当 d > 1 的时候，此时求出来的 xyz 会比之前大 1，这样计算 xyz * i 的时候就相当于多加了一个 i。此外，上边 i 溢出的问题，我们可以通过 long 类型解决。

public int countDigitOne(int n) {
    int count = 0;
    for (long k = 1; k <= n; k *= 10) {
        // xyzdabc
        int abc = n % k;
        int xyzd = n / k;
        int d = xyzd % 10;
        int xyz = (xyzd + 8) / 10;
        count += xyz * k;
        if (d == 1) {
            count += abc + 1;
        }
    }
    return count;
}

当然，还可以进一步省去xyz 和 d 这两个变量。

public int countDigitOne(int n) {
    int count = 0;

    for (long k = 1; k <= n; k *= 10) {
        long r = n / k, m = n % k;
        // sum up the count of ones on every place k
        count += (r + 8) / 10 * k + (r % 10 == 1 ? m + 1 : 0);
    }

    return count;
}