Dynamic Routing Between Capsules 笔记

胶囊神经网络，路由机制，capsule network，capsnet

参考资料

1.论文：Sabour S, Frosst N, Hinton G E. Dynamic routing between capsules[J]. Advances in neural information processing systems, 2017, 30.

2.讲解视频：Capsule Networks (CapsNets) – Tutorial: https://www.youtube.com/watch?v=pPN8d0E3900
该视频的b站转载: https://www.bilibili.com/video/BV1RW411W7rv
Hinton亲自称赞该视频： “This is an amazingly good video. I wish I could explain capsules that well.”

3.讲解博客：“Understanding Dynamic Routing between Capsules (Capsule Networks)”：https://jhui.github.io/2017/11/03/Dynamic-Routing-Between-Capsules/
该博客的csdn翻译转载：https://blog.csdn.net/bhneo/article/details/79391469

4.pytorch代码： https://github.com/adambielski/CapsNet-pytorch

简介

胶囊：描述（探测）某一特征的一组神经元。向量长度代表某特征出现的概率，向量方向体现了实例化参数。

作者使用 iterative routing-by-agreement mechanism 来传输胶囊的参数，并达到了很好的效果。高层胶囊向量由低层胶囊向量通过转移矩阵然后加权相加变换而来，可以提炼出更抽象的特征。

胶囊的路由（routing）机制

作者想要使用输出向量的模长来代表某一特征出现的概率，并使用了squashing function 来达到这一目的。
$$squash(x)=\frac{||x|{|}^2}{1+||x|{|}^2}\frac{x}{||x||}$$
对于不是第一层的胶囊$j$，我们设它接收到的前胶囊的总输入为$s_j$，我们可以使用如下方法来传输：

设$u_i$是前胶囊的输出，我们首先通过乘一个参数得到“预测向量”（prediction vectors）${\hat{u}}_{j|i}$ ，即
$${\hat{u}}_{j|i}=W_{ij}{u}_i$$
这一步如果将胶囊看作神经元，类似神经网络的全连接层，不同的是，下一步我们不只是将所有的 ${\hat{u}}_{j|i}$ 简单相加，而是继续给它增加一个权重 $c_{ij}$ ，使系统学习到低层胶囊对高层胶囊影响的大小。

需要注意，这里如果 $u_i$ 是标量，那么这两个参数可以简化为一个参数。而这里 $u_i$ 是矢量，我们可以理解为 $W_{ij}$ 调整了胶囊内部的权重，$c_{ij}$ 调节了胶囊间的权重。

现在只剩下一个问题待解决，那就是我们如何求权重 $c_{ij}$ ？答案也是这篇文章的精髓，路由机制：

路由机制的大概想法就是，增加最“像”输出的那个预测向量的权重，某种意义上是一种“注意”，达到了类似池化的效果，但是也并没有损失过多信息。

margin loss

目的：当某一特征（在这篇文章中使digit）出现，则输出向量的模长$||v_k||$尽量长（靠近1）

作者构造了如下损失函数：
$$L_k=T_k\max (0,m^{+}-||v_k||{)}^2+\lambda (1-T_k)\max (0,||v_k||-m^{-}{)}^2$$
这里 $T_k=1$ 当第k类特征存在于该样本中，其余情况 $T_k=0$ ，$m^{+}=0.9$ 和 $m^{-}=0.1$ 是阈值，更直观的，这个损失函数可以重写成：
$$L(k)=\{\begin{array}{ll}\max (0,m^{+}-||v_k||{)}^2,& k^{th}featureexists\\ \lambda \max (0,||v_k||-m^{-}{)}^2,& k^{th}featuredoesnotexist\end{array}$$

CapsNet网络结构

整体

• 卷积层
• primarycaps
• digitcaps

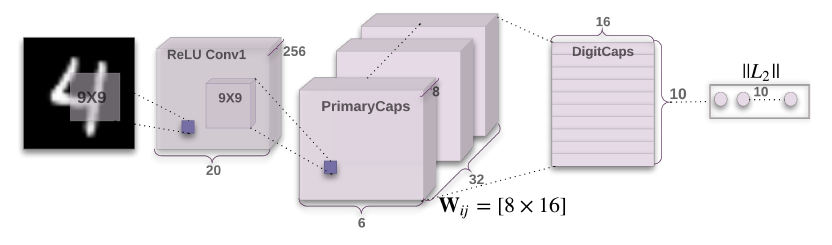
卷积层

普通二维卷积

primarycaps

二维卷积+重排+squash

digitcaps

作为primarycaps中胶囊的高层胶囊，使用前面介绍的传输机制搭建网络。

capsnets的正则方法

方法： 重建

目的： 鼓励digitcaps编码原始图像（类似自编码器的bottleneck层）

tricks：新增三个全连接层来解码，使用SE作为重构误差，并赋予重构误差一个较小的权重（相对于margin loss）

胶囊神经网络的优势

5.2： 对经过仿射变换的图像很稳定

6：分割高度重叠的digits效果很好

最后

以上就是老迟到汉堡为你收集整理的[笔记][胶囊神经网络]Dynamic Routing Between CapsulesDynamic Routing Between Capsules 笔记的全部内容，希望文章能够帮你解决[笔记][胶囊神经网络]Dynamic Routing Between CapsulesDynamic Routing Between Capsules 笔记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。