这里不讨论capsule的设计原理、优势以及特点等信息,只关注Capsule Net是如何实现的。
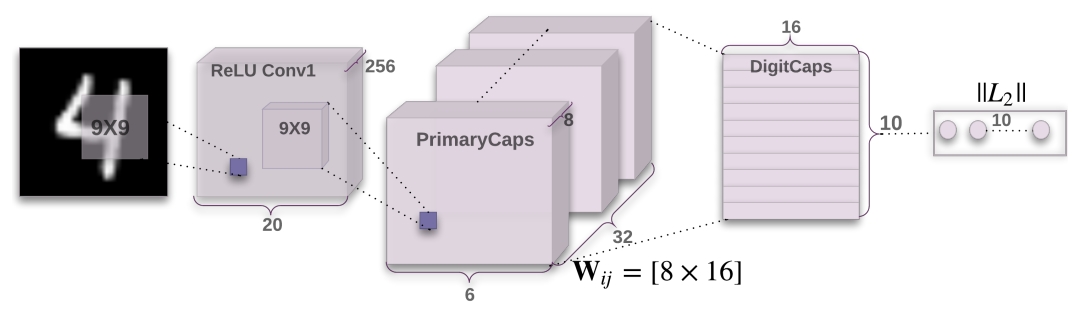
总体流程
- 在(28,28)的图片上进行卷积操作,得到feature map(20,20,256)
- concat 8个卷积得到的feature map,将其作为capsule(2048,8)
- 使用转移矩阵W将每个8维的capsule转换为10个16维的高级capsule(2048,10,16),再加权求和这2048个高级capsule得到DigitCaps(10,16),使用动态路由算法调整W.
- 将长度作为概率进行预测,并将概率最高的向量通过全连接层进行重构,分别计算分类损失和重构损失。
Conv1原图上提取低级特征
输入的mnist图片维度是(28,28),首先经过一个尺寸为(9,9)的卷积核,输出的feature map为(20,20,256)。
class ConvLayer(nn.Module):
def __init__(self, in_channels=1, out_channels=256, kernel_size=9):
super(ConvLayer, self).__init__()
self.conv = nn.Conv2d(in_channels=in_channels,
out_channels=out_channels,
kernel_size=kernel_size,
stride=1
)
def forward(self, x):
return F.relu(self.conv(x))
PrimaryCaps生成Capsules
capsules的产生同样是使用卷积得来的。论文中通过PrimaryCaps输出的capsule一共有32个,每个capsule尺寸是(6,6,8),于是卷积核被设计成(9,9),步长为2,输出通道数为32,每个卷积核输出的feature map为(6,6,32)。一共有8个这样的卷积核,也就意味着每个卷积核都产生capsule的一个维度。然后将这8个feature map拼接起来,得到的feature map为(8,32,6,6)。capsule的个数为2048,每个capsule是一个8维向量。最后,再将每个capsule进行squash操作,将每个向量的长度控制到0-1之间。
这个让我想起capsule与CNN的概念上的区别,CNN每个神经元是一个标量,而capsule的神经元是一个矢量,从上面这个操作我们能看到这个矢量是怎么得来的。如果说每个矢量的维度为8,那就设计8个卷积,将得到的8个feature map拼接起来,就将8个标量转换成一个8维的矢量,这是什么神仙操作?
class PrimaryCaps(nn.Module):
def __init__(self, num_capsules=8, in_channels=256, out_channels=32, kernel_size=9, num_routes=32 * 6 * 6):
super(PrimaryCaps, self).__init__()
self.num_routes = num_routes
self.capsules = nn.ModuleList([
nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=2, padding=0)
for _ in range(num_capsules)])
def forward(self, x):
u = [capsule(x) for capsule in self.capsules] # 8 *(32,6,6)
u = torch.stack(u, dim=1) # (8,32,6,6)
u = u.view(x.size(0), self.num_routes, -1) # (2048,8)
return self.squash(u)
def squash(self, input_tensor):
squared_norm = (input_tensor ** 2).sum(-1, keepdim=True)
output_tensor = squared_norm * input_tensor / ((1. + squared_norm) * torch.sqrt(squared_norm))
return output_tensor
低级Capsule转换成DigitCaps
生成高级capsule
从上面步骤已经得到capsule特征(2048,8),现在需要把它转化为更高级的capsule,由于是10分类,所以有10个capsule,每个capsule是16维的向量。每个低级capsule转换成高级capsule所需的矩阵W为(10,16,8),一共有2048个低级capsule,所以转换矩阵W为(2048,10,16,8)。得到的高级capsule为(2048,10,16),每个低级capsule都得到10个16维的向量。
动态路由算法生成DigitCaps
得到的高级capsule为(2048,10,16),就像在CNN最后的全连接层一样,所有的标量输入加权求和,激活后得到输出。这里权重矩阵为(2048,10),将这2048个高级capsule加权求和后得到特征经过squash激活后得到DigitCaps为(10,16)。为了更新权重矩阵的参数,计算2048个高级capsule与激活后DigitCaps的向量积,将其作为权重矩阵调整数值加到上一个权重矩阵上。
class DigitCaps(nn.Module):
def __init__(self, num_capsules=10, num_routes=32 * 6 * 6, in_channels=8, out_channels=16):
super(DigitCaps, self).__init__()
self.in_channels = in_channels
self.num_routes = num_routes
self.num_capsules = num_capsules
# [1, 2048, 10, 16, 8]
self.W = nn.Parameter(torch.randn(1, num_routes, num_capsules, out_channels, in_channels))
def forward(self, x):
batch_size = x.size(0)
x = torch.stack([x] * self.num_capsules, dim=2).unsqueeze(4) # (2048,10,8,1)
W = torch.cat([self.W] * batch_size, dim=0)
u_hat = torch.matmul(W, x)
b_ij = Variable(torch.zeros(1, self.num_routes, self.num_capsules, 1)) # (2048,10,1)
if USE_CUDA:
b_ij = b_ij.cuda()
num_iterations = 3
for iteration in range(num_iterations):
c_ij = F.softmax(b_ij, dim=1)
c_ij = torch.cat([c_ij] * batch_size, dim=0).unsqueeze(4) # (2048,10,1,1)
s_j = (c_ij * u_hat).sum(dim=1, keepdim=True)
v_j = self.squash(s_j)
if iteration < num_iterations - 1:
a_ij = torch.matmul(u_hat.transpose(3, 4), torch.cat([v_j] * self.num_routes, dim=1))
b_ij = b_ij + a_ij.squeeze(4).mean(dim=0, keepdim=True)
return v_j.squeeze(1)
def squash(self, input_tensor):
squared_norm = (input_tensor ** 2).sum(-1, keepdim=True)
output_tensor = squared_norm * input_tensor / ((1. + squared_norm) * torch.sqrt(squared_norm))
return output_tensor
DigitCaps解码重构
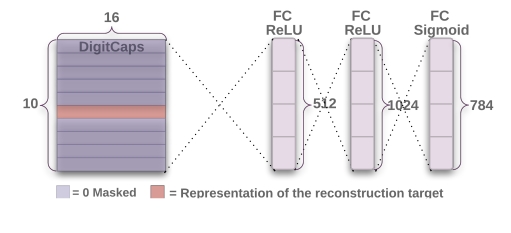
10个16维的向量,每个向量长度代表其存在概率,于是概率最大的向量就是预测结果。并且将这个向量输入到3层全连接层得到784维的向量表示重构的图片。
class Decoder(nn.Module):
def __init__(self, input_width=28, input_height=28, input_channel=1):
super(Decoder, self).__init__()
self.input_width = input_width
self.input_height = input_height
self.input_channel = input_channel
self.reconstraction_layers = nn.Sequential(
nn.Linear(16 * 10, 512),
nn.ReLU(inplace=True),
nn.Linear(512, 1024),
nn.ReLU(inplace=True),
nn.Linear(1024, self.input_height * self.input_height * self.input_channel),
nn.Sigmoid()
)
def forward(self, x, data):
classes = torch.sqrt((x ** 2).sum(2)) # (10,1)计算每个向量的长度
classes = F.softmax(classes, dim=0) # (10,1) 通过长度计算每个类别的概率
_, max_length_indices = classes.max(dim=1) # 找到预测概率最大的类别
# one hot编码
masked = Variable(torch.sparse.torch.eye(10))
if USE_CUDA:
masked = masked.cuda()
masked = masked.index_select(dim=0, index=Variable(max_length_indices.squeeze(1).data))
# 找到长度最长的向量进行重构
t = (x * masked[:, :, None, None]).view(x.size(0), -1)
reconstructions = self.reconstraction_layers(t) # (784)
reconstructions = reconstructions.view(-1, self.input_channel, self.input_width, self.input_height)
return reconstructions, masked
损失计算
分类损失
由于这里是使用向量的长度来表示预测的概率,所以希望正确类别的DigitCap能够长度更长,其他类别的capsule长度更短,作者设计了margin loss.
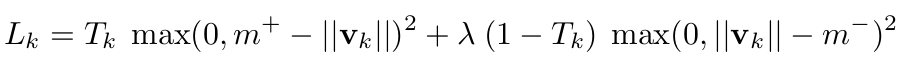
def margin_loss(self, x, labels, size_average=True):
batch_size = x.size(0)
v_c = torch.sqrt((x ** 2).sum(dim=2, keepdim=True))
left = F.relu(0.9 - v_c).view(batch_size, -1)
right = F.relu(v_c - 0.1).view(batch_size, -1)
loss = labels * left + 0.5 * (1.0 - labels) * right
loss = loss.sum(dim=1).mean()
return loss
重构损失
这里直接简单地计算重构的图片与原始图片每个像素的均方误差。并且这个损失在总的损失中权重只有0.0005.
def reconstruction_loss(self, data, reconstructions):
loss = self.mse_loss(reconstructions.view(reconstructions.size(0), -1), data.view(reconstructions.size(0), -1))
return loss * 0.0005
最后
以上就是爱笑白云最近收集整理的关于Pytorch实现CapsuleNet总体流程Conv1原图上提取低级特征PrimaryCaps生成Capsules低级Capsule转换成DigitCapsDigitCaps解码重构损失计算的全部内容,更多相关Pytorch实现CapsuleNet总体流程Conv1原图上提取低级特征PrimaryCaps生成Capsules低级Capsule转换成DigitCapsDigitCaps解码重构损失计算内容请搜索靠谱客的其他文章。








发表评论 取消回复