0 前言
昨天的面试官讲了利用自动驾驶激光雷达数据探测路上行人、车辆问题的局部空间关系的见解,提到了Vector向量多方位,多角度问题,我感觉和Capsule里的Vector有相似之处,但是面试官认为Hinton的Capsule有很多局限,在应用上目前只用在了mnist数据集上,并且建议我再好好读读Hinton的这篇论文。今年5月份时候我大概花了两三天看这个网络的讲解,后来仍然是一知半解就搁置了,现在就再好好的学习一下这篇论文吧。(面试表现不好,现在特别后悔。也感谢面试官一针见血指出我的问题)。
1. 论文理解
摘要翻译
Capsules是一组神经元,其活动向量(activity vector)代表特定类型实体的实例化参数,例如对象或对象部分。我们使用活动向量的长度表示实体存在的概率。它的方向表示实例化参数。一级活动Capsule通过变换矩阵进行预测,用于高级Capsule的参数实例化。当多个预测一致时,更高级别的Capsule被激活。经过这样特殊的训练,多层Capsule系统在MNIST上实现了最先进的性能,并且在识别高度重叠数字上更加优于卷积网络。为了实现这些效果,我们使用一个迭代的“按协议路由”机制:较低级别的Capsule喜欢将其输出发送到较高级别的Capsule,其活动向量具有大的标量积,而预测来自较低级别的胶囊。
重点理解
Capsule 是一组神经元,其输入输出向量表示特定实体类型的实例化参数(即特定物体、概念实体等出现的概率与某些属性)。我们使用输入输出向量的长度表征实体存在的概率,向量的方向表示实例化参数(即实体的某些图形属性)。同一层级的 capsule 通过变换矩阵对更高级别的 capsule 的实例化参数进行预测。当多个预测一致时(本论文使用动态路由使预测一致),更高级别的 capsule 将变得活跃。
Capsule 是一个高维向量,模长表示概率,方向表示属性。Hinton采用Squashing的非线性函数作为capsule的激活函数
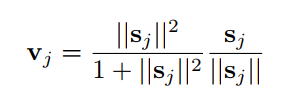
其中 v_j 为 Capsule j 的输出向量,s_j 为上一层所有 Capsule 输出到当前层 Capsule j 的向量加权和。 即 s_j 为 Capsule j 的输入向量。
- 该非线性函数前一部分是输入向量 s_j 的缩放尺度,后一部分是输入向量的单位向量s_j.
Capsule_j的输入向量 s_j的获取计算,是两层间的传播与联系方式。S_j计算过程分为两步,线性组合 和 Routing:
- 下图左式是Routing,右式是线性组合
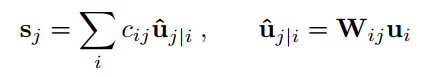
capsule层级结构图
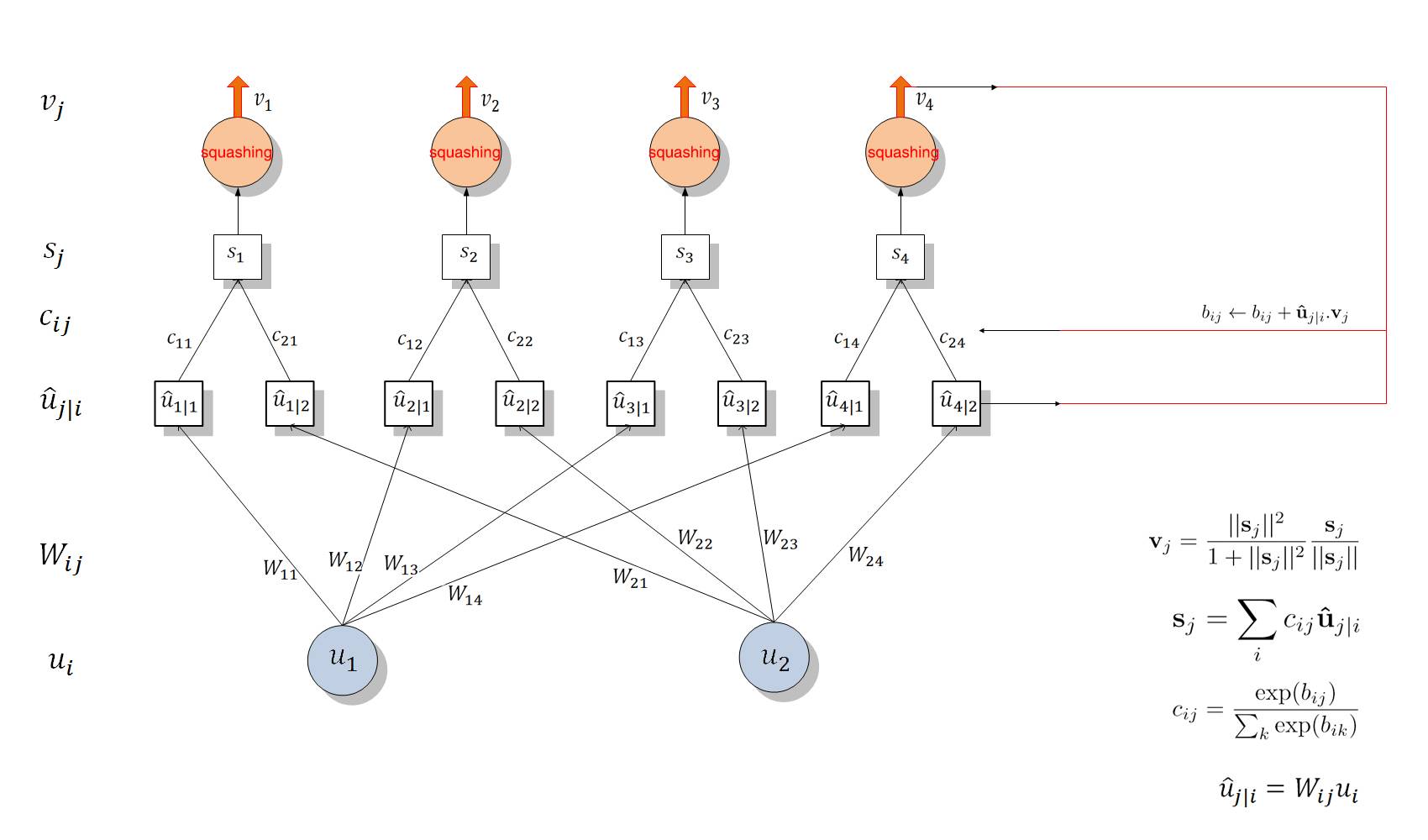
该图展示了 Capsule 的层级结构与动态 Routing 的过程。最下面的层级 u_i 共有两个 Capsule 单元,该层级传递到下一层级 v_j 共有四个 Capsule。u_1 和 u_2 是一个向量,即含有一组神经元的 Capsule 单元,它们分别与不同的权重 W_ij(同样是向量)相乘得出 u_j|i hat。例如 u_1 与 W_12 相乘得出预测向量 u_2|1 hat。随后该预测向量和对应的「耦合系数」c_ij 相乘并传入特定的后一层 Capsule 单元。不同 Capsule 单元的输入 s_j 是所有可能传入该单元的加权和,即所有可能传入的预测向量与耦合系数的乘积和。随后我们就得到了不同的输入向量 s_j,将该输入向量投入到「squashing」非线性函数就能得出后一层 Capsule 单元的输出向量 v_j。然后我们可以利用该输出向量 v_j 和对应预测向量 u_j|i hat 的乘积更新耦合系数 c_ij,这样的迭代更新不需要应用反向传播。
动态路由算法流程:

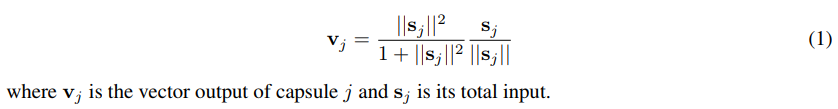


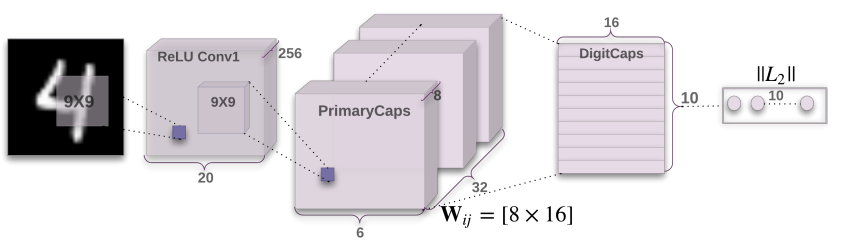
网络架构
第一层卷积层,输入:28*28; 输出:20*20*256
(使用256个9*9大小、步长为1的卷积核,该层拥有20*20*256个神经元)
第二层卷积层(主胶囊层),输入:20*20*256 ; 输出:6*6*8*32
(使用32个9*9大小、步长为2的卷积核,执行8遍,该层拥有6*6*32个胶囊)
第三层全连接层(数字胶囊层),输入:6*6*8*32 ; 输出:10*16 (拥有10个胶囊)
损失函数和最优化
耦合系数 c_ij 是通过一致性 Routing 进行更新的,但是整个网络其它的卷积参数和 Capsule 内的 W_ij 都需要根据损失函数进行反向更新。
作者采用了 SVM 中常用的 Margin loss,该损失函数的表达式为:
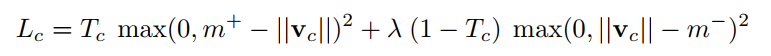
- 其中 c 是分类类别,T_c 为分类的指示函数(c 存在为 1,c 不存在为 0),m+ 为上边界,m- 为下边界。此外,v_c 的模即向量的 L2 距离。
- 对每一个表征数字 k 的 Capsule 分别给出单独的 Margin loss。
- 实例化向量的长度来表示 Capsule 要表征的实体是否存在。
重构与表征
Hinton 一直坚持的一个理念是,一个好的robust的模型,一定能够有重构的能力(”让模型说话“)。这点是有道理的,因为如果能够重构,我们至少知道模型有了一个好的表示,并且从重构结果中我们可以看出模型存在的问题。之前说过,capsule 的一个重要假设是每个 capsule 的向量可以表征一个实例。怎么来检验这个假设呢?一个方法就是重构。
重构的时候,我们单独取出需要重构的向量,扔到后面的网络中重构。当然后面的重构网络需要训练。利用预测出来的Capsules,重新构建出该类别的图像
文章中使用额外的重构损失(reconstruction loss)来促进 DigitCaps 层对输入数字图片进行编码:
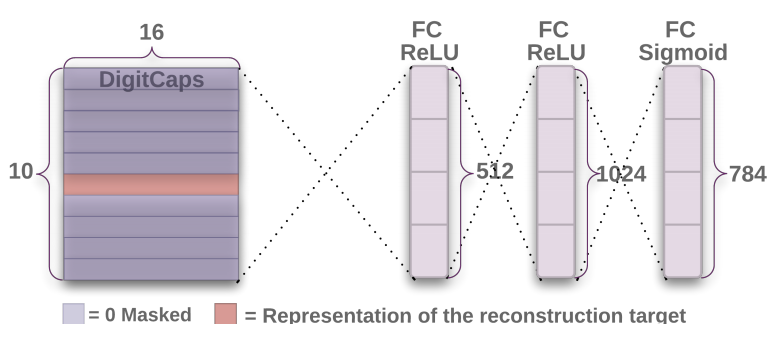
原图片可能数字重叠覆盖,导致预测出来的10个Capsules中部分Capsules的模都很大,所以重构单个数字图片时候,需要将其他Capsule进行Mask遮住,让有代表的Capsules去重构图片。损失函数通过计算在最后的 FC Sigmoid 层采用的输出像素点与原始图像像素点间的欧几里德距离作为损失函数。
为防止重构损失主导了整体损失(从而体现不出Margin loss作用),作者还按 0.0005 的比例缩小重构损失。
相比Softmax,Capsules不受多类别重叠的干扰,非常适合做单样本预测多类别的工作。
为什么Capsule没有在工业界引起更多关注?Capsules的应用点在哪里?
- 很难在其它大型数据集上应用
ImageNet 很难做重叠图像的实验(现实图片重叠的情况下本来就很难辨认,即使实现了也很难可视化),这点手写数字几乎是最理想的方案。
第二点是,在此实验的配置下,做 ImageNet 是自杀行为。因为 Capsules 假设是每个 Capsule 能够代表一个实例,本论文实现的动态路由方案比较naive,根本不能满足这么多的 Capsule 数量,何必做不符合自己假设的实验呢?其实文章作者知道这点,还是强行试了试 cifar10,果然效果不好(和最初应用到cifar10的CNN效果差不多)。
- 动态路由方案的缺陷
按照 Capsules 的假设,在当前方案下,训练 ImageNet,估计至少要用长度100的向量来表征一个物体吧(可能还是不够)。假设我们卷积层保持 256 * 256 的长宽,256个独立的 Capsules 分组,那么一层就有 16777216 个 Capsules,我们不管其他的,就看最后输出1000个分类,需要1000个Capsules(假设向量长度还是100个元素),那么参数占用内存(设类型为float32)就是 16777216 * 1000 * (100*100*4)= 671088640000000 = 671.08864 TB(不计路由等部分)。实际训练中内存还会数倍于这个数字,至少要翻一倍,到1.7 PB左右。如果你要单独用GPU放下这一层,就需要 80000 张 Titan X Pascal,更别提整个网络的参数量。如此多的参数显然是因为全连接的动态路由造成的。
参考网址
《Dynamic Routing Between Capsules》
CapsulesNet 的解析及整理
2. 代码理解
以下部分代码来自机器之心:先读懂CapsNet架构然后用TensorFlow实现:全面解析Hinton提出的Capsule
以下定义构建 CapsNet 后面两层的方法。在 CapsNet 架构中,我们能访问该类中的对象和方法构建 PrimaryCaps 层和 DigitCaps 层。
#通过定义类和对象的方式定义Capssule层级
class CapsLayer(object):
''' Capsule layer 类别参数有:
Args:
input: 一个4维张量
num_outputs: 当前层的Capsule单元数量
vec_len: 一个Capsule输出向量的长度
layer_type: 选择'FC' 或 "CONV", 以确定是用全连接层还是卷积层
with_routing: 当前Capsule是否从较低层级中Routing而得出输出向量
Returns:
一个四维张量
'''
def __init__(self, num_outputs, vec_len, with_routing=True, layer_type='FC'):
self.num_outputs = num_outputs
self.vec_len = vec_len
self.with_routing = with_routing
self.layer_type = layer_type
def __call__(self, input, kernel_size=None, stride=None):
'''
当“Layer_type”选择的是“CONV”,我们将使用 'kernel_size' 和 'stride'
'''
# 开始构建卷积层
if self.layer_type == 'CONV':
self.kernel_size = kernel_size
self.stride = stride
# PrimaryCaps层没有Routing过程
if not self.with_routing:
# 卷积层为 PrimaryCaps 层(CapsNet第二层), 并将第一层卷积的输出张量作为输入。
# 输入张量的维度为: [batch_size, 20, 20, 256]
assert input.get_shape() == [batch_size, 20, 20, 256]
#从CapsNet输出向量的每一个分量开始执行卷积,每个分量上执行带32个卷积核的9×9标准卷积
capsules = []
for i in range(self.vec_len):
# 所有Capsule的一个分量,其维度为: [batch_size, 6, 6, 32],即6×6×1×32
with tf.variable_scope('ConvUnit_' + str(i)):
caps_i = tf.contrib.layers.conv2d(input, self.num_outputs,
self.kernel_size, self.stride,
padding="VALID")
# 将一般卷积的结果张量拉平,并为添加到列表中
caps_i = tf.reshape(caps_i, shape=(batch_size, -1, 1, 1))
capsules.append(caps_i)
# 为将卷积后张量各个分量合并为向量做准备
assert capsules[0].get_shape() == [batch_size, 1152, 1, 1]
# 合并为PrimaryCaps的输出张量,即6×6×32个长度为8的向量,合并后的维度为 [batch_size, 1152, 8, 1]
capsules = tf.concat(capsules, axis=2)
# 将每个Capsule 向量投入非线性函数squash进行缩放与激活
capsules = squash(capsules)
assert capsules.get_shape() == [batch_size, 1152, 8, 1]
return(capsules)
if self.layer_type == 'FC':
# DigitCaps 带有Routing过程
if self.with_routing:
# CapsNet 的第三层 DigitCaps 层是一个全连接网络
# 将输入张量重建为 [batch_size, 1152, 1, 8, 1]
self.input = tf.reshape(input, shape=(batch_size, -1, 1, input.shape[-2].value, 1))
with tf.variable_scope('routing'):
# 初始化b_IJ的值为零,且维度满足: [1, 1, num_caps_l, num_caps_l_plus_1, 1]
b_IJ = tf.constant(np.zeros([1, input.shape[1].value, self.num_outputs, 1, 1], dtype=np.float32))
# 使用定义的Routing过程计算权值更新与s_j
capsules = routing(self.input, b_IJ)
#将s_j投入 squeeze 函数以得出 DigitCaps 层的输出向量
capsules = tf.squeeze(capsules, axis=1)
return(capsules)下面是整个 CapsNet 的架构与推断过程代码,我们需要从 MNIST 抽出图像并投入到以下定义的方法中,该批量的图像将先通过三层 CapsNet 网络输出 10 个类别向量,每个向量有 16 个元素,且每个类别向量的长度为输出图像是该类别的概率。随后,我们会将一个向量投入到重构网络中构建出该向量所代表的图像。
# 以下定义整个 CapsNet 的架构与正向传播过程
class CapsNet():
def __init__(self, is_training=True):
self.graph = tf.Graph()
with self.graph.as_default():
if is_training:
# 获取一个批量的训练数据
self.X, self.Y = get_batch_data()
self.build_arch()
self.loss()
# t_vars = tf.trainable_variables()
self.optimizer = tf.train.AdamOptimizer()
self.global_step = tf.Variable(0, name='global_step', trainable=False)
self.train_op = self.optimizer.minimize(self.total_loss, global_step=self.global_step) # var_list=t_vars)
else:
self.X = tf.placeholder(tf.float32,
shape=(batch_size, 28, 28, 1))
self.build_arch()
tf.logging.info('Seting up the main structure')
# CapsNet 类中的build_arch方法能构建整个网络的架构
def build_arch(self):
# 以下构建第一个常规卷积层
with tf.variable_scope('Conv1_layer'):
# 第一个卷积层的输出张量为: [batch_size, 20, 20, 256]
# 以下卷积输入图像X,采用256个9×9的卷积核,步幅为1,且不使用
conv1 = tf.contrib.layers.conv2d(self.X, num_outputs=256,
kernel_size=9, stride=1,
padding='VALID')
assert conv1.get_shape() == [batch_size, 20, 20, 256]
# 以下是原论文中PrimaryCaps层的构建过程,该层的输出维度为 [batch_size, 1152, 8, 1]
with tf.variable_scope('PrimaryCaps_layer'):
# 调用前面定义的CapLayer函数构建第二个卷积层,该过程相当于执行八次常规卷积,
# 然后将各对应位置的元素组合成一个长度为8的向量,这八次常规卷积都是采用32个9×9的卷积核、步幅为2
primaryCaps = CapsLayer(num_outputs=32, vec_len=8, with_routing=False, layer_type='CONV')
caps1 = primaryCaps(conv1, kernel_size=9, stride=2)
assert caps1.get_shape() == [batch_size, 1152, 8, 1]
# 以下构建 DigitCaps 层, 该层返回的张量维度为 [batch_size, 10, 16, 1]
with tf.variable_scope('DigitCaps_layer'):
# DigitCaps是最后一层,它返回对应10个类别的向量(每个有16个元素),该层的构建带有Routing过程
digitCaps = CapsLayer(num_outputs=10, vec_len=16, with_routing=True, layer_type='FC')
self.caps2 = digitCaps(caps1)
# 以下构建论文图2中的解码结构,即由16维向量重构出对应类别的整个图像
# 除了特定的 Capsule 输出向量,我们需要蒙住其它所有的输出向量
with tf.variable_scope('Masking'):
#mask_with_y是否用真实标签蒙住目标Capsule
mask_with_y=True
if mask_with_y:
self.masked_v = tf.matmul(tf.squeeze(self.caps2), tf.reshape(self.Y, (-1, 10, 1)), transpose_a=True)
self.v_length = tf.sqrt(tf.reduce_sum(tf.square(self.caps2), axis=2, keep_dims=True) + epsilon)
# 通过3个全连接层重构MNIST图像,这三个全连接层的神经元数分别为512、1024、784
# [batch_size, 1, 16, 1] => [batch_size, 16] => [batch_size, 512]
with tf.variable_scope('Decoder'):
vector_j = tf.reshape(self.masked_v, shape=(batch_size, -1))
fc1 = tf.contrib.layers.fully_connected(vector_j, num_outputs=512)
assert fc1.get_shape() == [batch_size, 512]
fc2 = tf.contrib.layers.fully_connected(fc1, num_outputs=1024)
assert fc2.get_shape() == [batch_size, 1024]
self.decoded = tf.contrib.layers.fully_connected(fc2, num_outputs=784, activation_fn=tf.sigmoid)
# 定义 CapsNet 的损失函数,损失函数一共分为衡量 CapsNet准确度的Margin loss
# 和衡量重构图像准确度的 Reconstruction loss
def loss(self):
# 以下先定义重构损失,因为DigitCaps的输出向量长度就为某类别的概率,因此可以借助计算向量长度计算损失
# [batch_size, 10, 1, 1]
# max_l = max(0, m_plus-||v_c||)^2
max_l = tf.square(tf.maximum(0., m_plus - self.v_length))
# max_r = max(0, ||v_c||-m_minus)^2
max_r = tf.square(tf.maximum(0., self.v_length - m_minus))
assert max_l.get_shape() == [batch_size, 10, 1, 1]
# 将当前的维度[batch_size, 10, 1, 1] 转换为10个数字类别的one-hot编码 [batch_size, 10]
max_l = tf.reshape(max_l, shape=(batch_size, -1))
max_r = tf.reshape(max_r, shape=(batch_size, -1))
# 计算 T_c: [batch_size, 10],其为分类的指示函数
# 若令T_c = Y,那么对应元素相乘就是有类别相同才会有非零输出值,T_c 和 Y 都为One-hot编码
T_c = self.Y
# [batch_size, 10], 对应元素相乘并构建最后的Margin loss 函数
L_c = T_c * max_l + lambda_val * (1 - T_c) * max_r
self.margin_loss = tf.reduce_mean(tf.reduce_sum(L_c, axis=1))
# 以下构建reconstruction loss函数
# 这一过程的损失函数通过计算FC Sigmoid层的输出像素点与原始图像像素点间的欧几里德距离而构建
orgin = tf.reshape(self.X, shape=(batch_size, -1))
squared = tf.square(self.decoded - orgin)
self.reconstruction_err = tf.reduce_mean(squared)
# 构建总损失函数,Hinton论文将reconstruction loss乘上0.0005
# 以使它不会主导训练过程中的Margin loss
self.total_loss = self.margin_loss + 0.0005 * self.reconstruction_err
# 以下输出TensorBoard
tf.summary.scalar('margin_loss', self.margin_loss)
tf.summary.scalar('reconstruction_loss', self.reconstruction_err)
tf.summary.scalar('total_loss', self.total_loss)
recon_img = tf.reshape(self.decoded, shape=(batch_size, 28, 28, 1))
tf.summary.image('reconstruction_img', recon_img)
self.merged_sum = tf.summary.merge_all()完整代码地址:https://github.com/naturomics/CapsNet-Tensorflow
最后
以上就是整齐绿草最近收集整理的关于学习笔记-《Dynamic Routing Between Capsules》的全部内容,更多相关学习笔记-《Dynamic内容请搜索靠谱客的其他文章。








发表评论 取消回复