01 - 大O表示法

84 阅读 0 评论 56 点赞

我是靠谱客的博主复杂马里奥，最近开发中收集的这篇文章主要介绍01 - 大O表示法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

使用它来估算算法的好坏

概念：

一般用大O表示法来描述复杂度，它表示的是数据规模n 对应的复杂度。
解读：当给了一个形参n, 它的对应复杂度是多少。

估算下面方法的复杂度

Java 版本

public static void test1(int n) {
	if (n > 10) {
		System.out.println("n > 10");
	} else if if (n > 5) {
		System.out.println("n > 5");
	}  else {
		System.out.println("n <= 5");
	}

	for (int i = 0; i < 4; i++) {
		System.out.println("test");
	}

swift 版本

/// 估算方法的复杂度
    public func test1(n: Int) {
        if n > 10 {
            print("n > 10")
        } else if n > 5 {
            print("n > 5")
        } else {
            print("n <= 5")
        }
        
        for _ in 0..<4 {
            print("test")
        }
    }

整个 if else 判断是1 次
for 循环是 1 + 4 + 4 + 4
int i = 0 ；是1次
i < 4 ; 是 4 次
i++ ；是 4 次
system 输出时 4 次

代码如下：
Java 版本

public static void test3(int n) {
	for (int i = 0; i < n ; i++) {
		for (int j = 0; j < n; j++) {
			System.out.println("test");
		}
	}
}

Swift 版本

public func test3 (n: Int) {
        for i in 0..<n {
            for j in 0..<n {
                print("test - (i) (j)")
            }
        }
    }

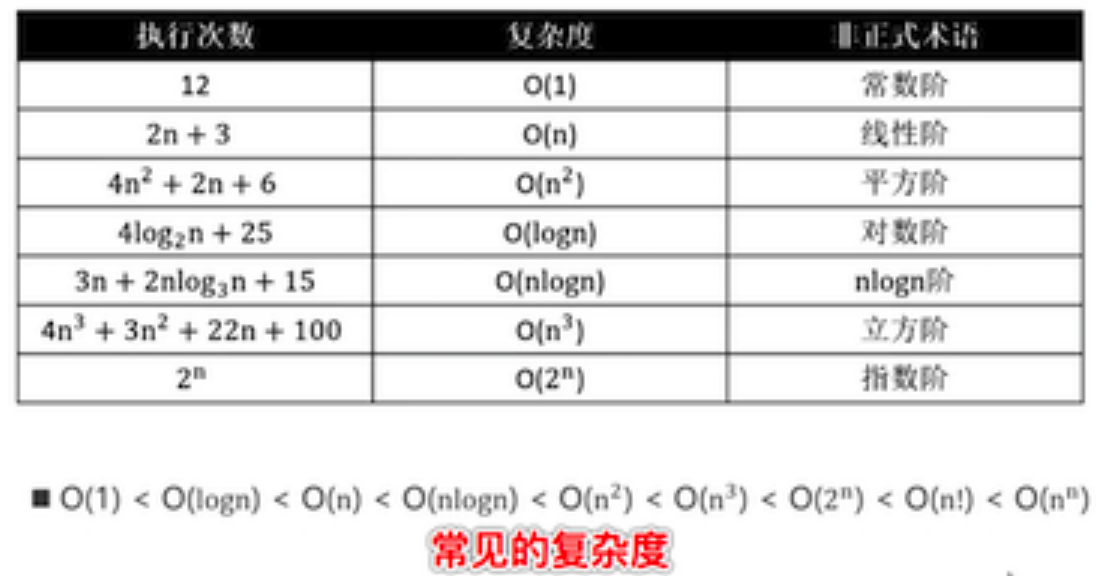
可以看到，这样估算时间非常的麻烦，这个时候就可以用大O表示法来估算，它可以忽略常数、系数、低阶

9 >> O(1)
只要是常数，以后的估算就是 O(1)
这是因为，当 n 非常大的时候，就不会有太大的差别了。
2n + 3 >> O(n)
有 n 的时候，忽略常数3. 叫做 O(n)
n的平方 + 2n + 6 >> O(n的平方)
有 n^2 时，忽略 n （所以这里忽略了 2n）. 叫做 O(n^2)
4(n^3) + 3(n^2) + 22n + 100 >> O(n^3)
有 n^3 时，忽略 n的平方，所以这里忽略了 3 * n的平方，叫做 O( n^3)
n的3次方等价于 n^3

总结：

对数阶的细节
在这里插入图片描述

速度：常数 > logn > O(n) > O(nlogn) > O(n^2)

注意：大O表示法仅仅是一种粗略的分析模型，是一种估算，能帮助我们短时间内了解一个算法的执行效率。
在这里插入图片描述

O(1)
O(1)表示该算法的执行时间（或执行时占用空间）总是为一个常量，不论输入的数据集是大是小。

O(N)
O(N)表示一个算法的性能会随着输入数据的大小变化而线性变化。下面的例子同时也表明了大O表示法其实是用来描述一个算法的最差情况的：在for循环中，一旦程序找到了输入数据中与第二个传入的string匹配时，程序就会提前退出，然而大O表示法却总是假定程序会运行到最差情况（在这个例子中，意味着大O会表示程序全部循环完成时的性能）。

O(N^2)
O(N^2)表示一个算法的性能将会随着输入数据的增长而呈现出二次增长。最常见的算法就是对输入数据进行嵌套循环。如果嵌套层级不断深入的话，算法的性能将会变为O(N3)，O(N4)，以此类推。

O(2^N)
O(2^{N)表示一个算法的性能将会随着输入数据的每次增加而增大两倍。O(2}N)的增长曲线是一条爆炸式增长曲线——开始时较为平滑，但数据增长后曲线增长非常陡峭。一个典型的O(2^N)方法就是裴波那契数列的递归计算实现。

对数
要说明对数情况，稍稍有点复杂，因此我将使用一个非常通用的示例：
二分查找是一种用来在有序集合中进行查找的高效算法。二分查找从数据集的中间位置开始，然后用这个中间值和一个目标值进行比较。如果比较结果为相等，则程序返回成功。如果目标值大于中间值，程序会截取从中间值开始到最大值的那段数据集，并重复执行同样的查找方法。想死的，如果目标值小于中间值，程序将会继续在数据集中较小的那一半执行二分查找。二分查找程序会持续的将数据集对等分，以进入下一次循环，直到最终找到与目标值相等的数据后，程序就退出。
这类算法的性能就会被描述为O(logN)。正是通过这种不断对数据进行对等分的二分查找操作，使得二分查找算法的曲线从一个峰值开始，随着输入数据集的增长而慢慢的变得平缓。用例子来说明的话，例如一个包含10个输入数据的程序需要耗时一秒完成，则一个包含100个输入数据的程序就需要耗时两秒，然后一个包含1000个输入数据的程序就耗时三秒。加倍的输入数据对这类算法的性能结果影响非常小。基于如此，类似于二分查找的对数级算法在处理大量数据集时非常高效。
———————————————————————————————————————————————————————

空间复杂度