Mr.Yang的学习笔记------图的基本操作

图的基本操作（无向图）

1.两种遍历方法

1）深度优先搜索（DFS，Depth First Search）
当然初始的图没有被访问过，我们从某个顶点v开始访问，然后从v的相邻顶点开始访问，假设有v1，v2，v3，那么假设从v1开始，又要把v1的相邻顶点访问完，才能退回去访问v2和v3，其实就是一个递归问题。例子如下：

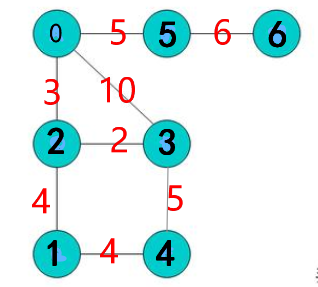
搜索结果为：0214356
2）广度优先搜索（BFS，Breadth First Search）
我们从某个顶点v开始访问，然后从v的相邻顶点开始访问，假设有v1，v2，v3，而v1相邻顶点有v4，v5，那么v访问之后，要先把v的相邻顶点v1，v2，v3访问完成之后再去访问v1，v2，v3的相邻顶点。1）中例子的广度优先搜索结果为：0235146

2.求单源最短路径

1. 从起点开始，查找所有起点的相邻顶点，并把连接它们的边权值作为起点到它们的距离(有平行边取最小值)。起点到起点的距离为0，其它不与起点直接相连的点距离为无穷大。
2. 遍历所有点，查找得到的结果中距离最小的那个点，然后再看所有与该点直接相连的点，计算该点到它们的最短距离(即从起点开始，经由该点到达的点的距离)。
3. 不断重复2中过程，直到每一个点都像2中那样计算过一遍。
   if(D[i]==0) {D[i]=D[v]+G.weight(v,i);}
   else
   {if(D[i]>D[v]+G.weight(v,i)) D[i]=D[v]+G.weight(v,i);}

3.判断是否有环

判断一个图是否有环，首先一点边数肯定要少于顶点数，其次就是边数少于顶点数也不一定没有环，比如：

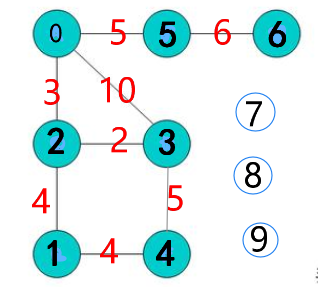
这种情况边数少于顶点数，但是有环，所以只有判断图的每一个连通图都满足边数少于顶点数，这样就没有环。
总结的一个公式：e（边数）+n（连通子图数）>v（顶点数）
这种情况有环。

4.例题

1.图的存储结构使用邻接矩阵。
2.创建图操作类，支持BFS遍历、DFS遍历、求单源最短路径、判断是否存在回路等四个功能，这些功能封装成图操作类的成员函数。
3.输入图的节点数n（不超过10个）、边数m，节点分别用0到n-1表示。
4.采用“起始节点，终止节点，权值”输入图的m条边，创建图。
5.输出从节点0开始的BFS遍历、DFS遍历节点遍历顺序。
6.输出从节点0到其余节点最短路径的长度，如果没有路经，输出0。

5.代码

#include <iostream> 
#include <conio.h>                  
using namespace std;

class Edge{                       //class edge 
public:
	int v1,v2,weight;
	Edge() {}
	Edge(int x,int y,int z) {v1=x;v2=y;weight=z;}
	~Edge() {}
	friend istream& operator >> (istream &in, Edge &e);
};
istream& operator >> (istream& input, Edge& e){
   input>>e.v1>>e.v2>>e.weight;
   return input;
}

class Graph{                 // class Graph
private:
	int numVertex,numEdge;
	int **matrix;
	int *mark;
public:
	Graph(int numVert){
		Init(numVert);
	}
	~Graph(){
		delete [] mark;
		for(int i=0;i<numVertex;i++)
			delete [] matrix[i];
		delete [] matrix;
	}
	void Init(int n){        //initailization of undirected graph
		int i;
		numVertex=n;
		numEdge=0;
		mark=new int[n];
		for(i=0;i<numVertex;i++)
			mark[i]=0;
		matrix=(int**) new int*[numVertex];
		for(i=0;i<numVertex;i++)
			matrix[i]= new int[numVertex];
		for(i=0;i<numVertex;i++)
			for(int j=0;j<numVertex;j++)
				matrix[i][j]=0;
	}
	int n() { return numVertex;}
	int e() { return numEdge;}
	int first(int v){
		for(int i=0;i<numVertex;i++)
			if(matrix[v][i]!=0)
				return i;
		return numVertex;
	}
	int next(int v,int w){
		for(int i=w+1;i<numVertex;i++)
			if(matrix[v][i]!=0)
				return i;
		return numVertex;
	}
	void setEdge(int v1,int v2,int wt){
		if(matrix[v1][v2]==0)
			numEdge++;
		matrix[v1][v2]=wt;
		matrix[v2][v1]=wt;
	}
	void delEdge(int v1,int v2){
		if(matrix[v1][v2]!=0)
			numEdge--;
		matrix[v1][v2]=0;
		matrix[v2][v1]=0;
	}
	bool isEdge(int i,int j){
		return matrix[i][j]!=0;
	}
	int weight(int v1,int v2){
		return matrix[v1][v2];
	}
	int getMark(int v){
		return mark[v];
	}
	void setMark(int v,int val){
		mark[v]=val;
	}
	void Initmark(){
		for(int i=0;i<this->n();i++)
			this->setMark(i,0);
	}
	void DFS1(int v){
		cout<<v<<" ";
		this->setMark(v,1);
		for(int w=this->first(v);w<this->n();w=this->next(v,w))
		{
			if(this->getMark(w)==0)
			{
				DFS1(w);
			}
		}		
	}
	void DFS(){                    // the DFS
		for(int i=0;i<this->n();i++){
			if(this->getMark(i)==0)
				DFS1(i);
		}
	}
	void BFS(int start,int *Q){   // the BFS
		int v,w,a=0;
		Q[a]=start;
		a++;
		this->setMark(start,1);
		for(int i=0;i<this->n();i++){
			v=i;
			if(this->getMark(v)==0){
				Q[a]=v;
				this->setMark(v,1);
				a++;
			}
			for(w=this->first(v);w<this->n();w=this->next(v,w))
				if(this->getMark(w)==0){
					this->setMark(w,1);
					Q[a]=w;
					a++;
				}
		}
		for(int i=0;i<a;i++)
			cout<<Q[i]<<" ";		
	}
	int Mindis(Graph& G,int *D,int start){ //the shortest distance
		int v,a=0,b,min,count=1;
		v=start;
		G.setMark(v,1);
		while(a==0){
			int F[G.n()];
			for(int i=0;i<G.n();i++)
				F[i]=-1;
			for(int i=0;i<G.n();i++){
				if(G.getMark(i)==0 && G.weight(v,i)!=0){
					if(D[i]==0) {D[i]=D[v]+G.weight(v,i);}
					else{
						if(D[i]>D[v]+G.weight(v,i)) D[i]=D[v]+G.weight(v,i);
					}
				}	
			}
			for(int k=0;k<G.n();k++){
				if(G.getMark(k)==0 && D[k]!=0){
					F[k]=D[k];
				}
			}
			for(int i=0;i<G.n();i++){
				if(F[i]!=-1){
					min=F[i];
					b=i;
					break;
				}
			}
			for(int i=0;i<G.n();i++){
				if(F[i]!=-1 && F[i]<min){
					min=F[i];
					b=i;
				}
			}
			G.setMark(b,1);
			v=b;
			if(this->first(v)>=this->n())
				count++;
			for(int w=this->first(v);w<this->n();w=this->next(v,w)){
				if(this->getMark(w)==0){
					a=0;
					break;
				}	
				else
					a=1;
			}	
		}
		for(int i=0;i<G.n();i++){
			if(this->getMark(i)==0)
				this->setEdge(0,i,0);
		}
		for(int t=1;t<G.n();t++){
			cout<<"0 "<<t<<" "<<D[t]<<endl;
		}
		return count;
	}
	void isCycle(Graph& G,int b){        //have or haven't cycle
		int a;
		a=b+this->e()-1;
		if(a>=this->n())
			cout<<"YES";
		else
			cout<<"NO";
	}
};

int main(){
	int sizeV,sizeE,b;
	cout<<"please enter the size of Vertex and Edge:"<<endl;
	cin>>sizeV>>sizeE;
	Graph G(sizeV);
	int Q[sizeV],D[sizeV]={0};
	cout<<"please enter the weight of the edge:"<<endl;
	for(int i=0;i<sizeE;i++){
		Edge E=Edge();
		cin>>E;
		G.setEdge(E.v1,E.v2,E.weight);
	}
	cout<<"the BFS is:"<<endl;
	G.BFS(0,Q);
	G.Initmark();
	cout<<endl;
	cout<<"the DFS is:"<<endl;
	G.DFS();
	G.Initmark();
	cout<<endl;
	cout<<"the shortest distance from 0 to others:"<<endl;
	b=G.Mindis(G,D,0);
	G.Initmark();
	cout<<"have a cycle:"<<endl;
	G.isCycle(G,b);
	G.~Graph();
}

6.结果

最后

以上就是风中铃铛为你收集整理的Mr.Yang的学习笔记------图的基本操作的全部内容，希望文章能够帮你解决Mr.Yang的学习笔记------图的基本操作所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。