- ???? 个人网站: 路遥叶子
- ???? 版权: 本文由【路遥叶子】原创、在CSDN首发、需要转载请联系博主
- ???? 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦
- ???? 想寻找共同成长的小伙伴,请点击【Java全栈开发社区】
目录
第三章 串与数组 
一、什么是串?
1. 串概述
2. 名词解释
3. 串的抽象类型(接口)
二、串的存储方式有那些?
三、顺序串
3.1 算法:基本功能
3.2 算法:扩容
3.3 算法:求子串
3.4 算法:插入
3.5 算法:删除
3.6 算法:比较
四、什么是模式匹配?
4.1 概述
4.2 Brute-Force算法:分析
4.3 Brute-Force算法:算法实现
4.4 KMP算法:动态演示
4.5 KMP算法:求公共前后缀
4.6KMP算法:求公共前后缀 next数组 -- 算法演示
4.7 KMP算法:求公共前后缀 next数组 -- 算法实现
4.8 KMP算法:算法实现
如果觉得文章对您有帮助,就拿起你的小手赶紧给博主点赞、评论、收藏一下吧~~~ 赶紧动起来,让我们一起加油学习。博主会不断推出更多优质文章哟
第三章 串与数组 
 一、什么是串?
一、什么是串?
 1. 串概述
1. 串概述
![]() 串,也称为
串,也称为字符串,是一个种特殊的线性表,由n(n>=0)个字符组成的有序序列。
 2. 名词解释
2. 名词解释
![]() 长度:包含的字符个数n。
长度:包含的字符个数n。
![]() 空串:n为0的串就是空串,不包含任何字符。
空串:n为0的串就是空串,不包含任何字符。
![]() 空白串:包含一个及以上(n>=1)空白字符的串,长度为空白字符的个数。
空白串:包含一个及以上(n>=1)空白字符的串,长度为空白字符的个数。
![]() 子串:串中任意连续的字符组成的子序列。
子串:串中任意连续的字符组成的子序列。
![]() 空串是任意串的子串。
空串是任意串的子串。
![]() 任意串是其自身的子串。“ABC”
任意串是其自身的子串。“ABC”
![]() 主串:包含子串的串。
主串:包含子串的串。
![]() 序号值:在之前的学习过程中称为“索引值”,字符在串中的位置。
序号值:在之前的学习过程中称为“索引值”,字符在串中的位置。
![]() 子串在主串中的位置:子串在主串中首次出现时的第一个字符在主串中的位置。
子串在主串中的位置:子串在主串中首次出现时的第一个字符在主串中的位置。
![]() 串相等:两个串的长度相同,且各个对应位置的字符相同。
串相等:两个串的长度相同,且各个对应位置的字符相同。
 3. 串的抽象类型(接口)
3. 串的抽象类型(接口)
public interface IString{
public void clear(); //串的清空
public boolean isEmpty(); //是否为空
public int length(); //串的长度,串中字符的个数
public char charAt(index); //返回第index个字符值
public IString substring(begin,end); //*获得子串[begin,end)
public IString insert(offset, str); //在第offset个字符之前插入str串
public IString delete(begin, end); //删除子串[begin,end)
public IString concat(IString str); //*把str串连接到当前串的后面
public int compareTo(IString str); //串的比较,相同返回0,否则返回正/负
public int indexOf(str, begin); //从start开始,返回str在串中位置,不存在返回-1
}------------------------------------------------------------------
 二、串的存储方式有那些?
二、串的存储方式有那些?
![]() 串的存储结构包括:顺序存储 和 链式存储。
串的存储结构包括:顺序存储 和 链式存储。
![]() 顺序存储:使用数组存放字符。
顺序存储:使用数组存放字符。
public class SeqString implements IString{
private char[] strvalue; // 字符数组,用于存放字符串信息
private int curlen; // 串的长度 current length
} ![]() 链式存储:使用链表存储。
链式存储:使用链表存储。
![]() 字符链表:每个结点只有一个字符的链表。
字符链表:每个结点只有一个字符的链表。
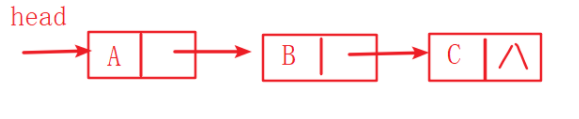
![]() 块链表:每个结点可以有多个字符。
块链表:每个结点可以有多个字符。

------------------------------------------------------------------
 三、顺序串
三、顺序串
 3.1 算法:基本功能
3.1 算法:基本功能
public class SeqString implements IString{
private char[] strvalue; // 字符数组,用于存放字符串信息
private int curlen; // 串的长度 current length
public void clear() { //清空
this.curlen = 0;
}
public boolean isEmpty() { //是否有空
return this.curlen == 0;
}
public int length() { //串的长度
return this.curlen;
}
public char charAt(int index) {
if(index < 0 || index >= curlen) {
throw new 字符串索引越界异常(); //String Index OutOfBounds Exception
}
return strvalue[index];
}
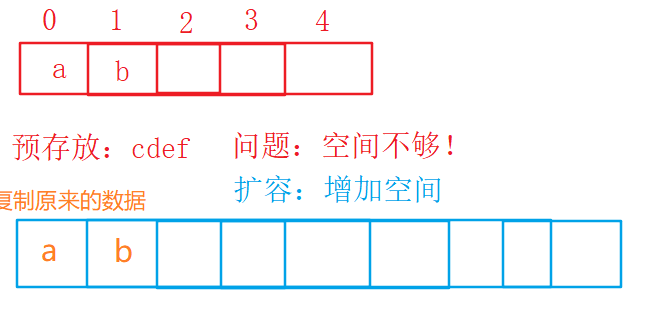
}  3.2 算法:扩容
3.2 算法:扩容
/**
* @param newCapacity 新容器大小
*/
public void allocate(int newCapacity) {
char[] temp = strvalue; // 存放原来的数据 ab数组
strvalue = new char[newCapacity]; // 给strValue重新赋一个更大数组的值
for(int i = 0; i < temp.length; i++) { // 拷贝数据
strvalue[i] = temp[i];
}
}  3.3 算法:求子串
3.3 算法:求子串
![]() 需求:"abcd".substring(1,3) --> "bc"
需求:"abcd".substring(1,3) --> "bc"
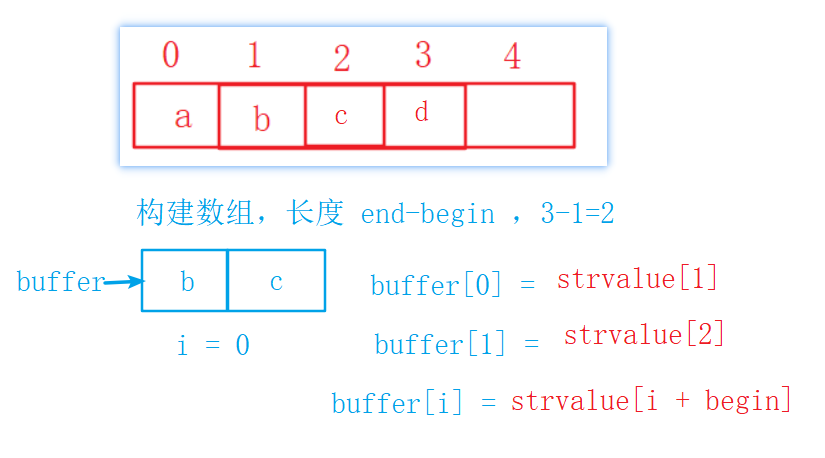
public IString substring(int begin , int end) {
// 1 两个参数校验
if(begin < 0) { // 1.1 begin 不能小于0
throw new StringIndexOutOfBoundsException("begin不能小于0");
}
if(end > curlen) { // 1.2 end 不能大于当前长度
throw new StringIndexOutOfBoundsException("end不能大于当前长度");
}
if(begin > end) { // 1.3
throw new StringIndexOutOfBoundsException("begin不能大于end");
}
// 2 优化:当前串直接返回
if(begin == 0 && end == curlen) {
return this;
}
// 3 核心算法
char[] buffer = new char[end - begin]; // 构建新数组
for(int i = 0 ; i < buffer.length ; i ++) { // 依次循环遍历新数组,一个一个赋值
buffer[i] = strvalue[i + begin];
}
return new SeqString(buffer); // 使用字符数组构建一个新字符串
}  3.4 算法:插入
3.4 算法:插入
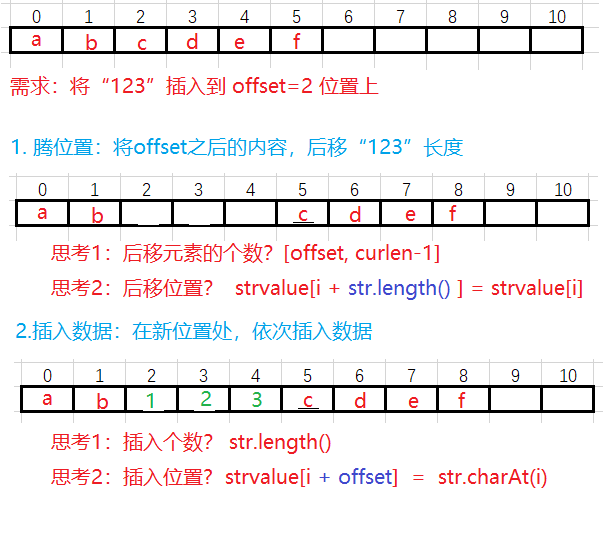
/** "abcdef".insert(2,"123").insert(...)
* @param offset 偏移量,插入的位置
* @param str 插入数据
*/
public IString insert (int offset, IString str) {
//1 校验
if(offset < 0 || offset > curlen) {
throw new StringIndexOutOfBoundsException("插入位置不合法");
}
//2 兼容:如果容器不够,需要扩容 当前长度 + 新字符串 > 容器长度
int newCount = curlen + str.length();
if( newCount > strvalue.length ) {
allocate(newCount); //扩容结果就是刚刚好,没有额外空间
}
// 3 核心
//3.1 核心1:从offset开始向后移动 str长度 个字符
for(int i = curlen-1 ; i >= offset ; i --) {
strvalue[i + str.length() ] = strvalue[i];
}
//3.2 核心2:依次插入
for(int i = 0; i < str.length() ; i ++) {
strvalue[i + offset] = str.charAt(i);
}
//3.3 设置数组长度
this.curlen = newCount;
return this;
}  3.5 算法:删除
3.5 算法:删除

/**
* @param begin 删除开始位置(含)
* @param end 删除结果位置(不含)
*/
public IString delete(int begin , int end) {
// 1 校验
// 1.1 begin 范围
if(begin < 0) {
throw new StringIndexOutOfBoundsException("begin不能小于0");
}
// 1.2 end 范围
if(end > curlen) {
throw new StringIndexOutOfBoundsException("end不能大于串长");
}
// 1.3 关系
if(begin > end) {
throw new StringIndexOutOfBoundsException("begin不能大于end");
}
// 2 核心:将后面内容移动到签名
// 2.1 移动
for(int i = 0 ; i < curlen - end ; i ++) {
strvalue[i + begin] = strvalue[i + end];
}
// 2.2 重新统计长度 (end-begin 需要删除串的长度)
curlen = curlen - (end-begin)
return this;
}  3.6 算法:比较
3.6 算法:比较

/**
* @param str 需要比较的串
* return
* >0 : 前面串值的值大于后面串
* =0 : 前面串值的值等于后面串
* <0 : 前面串值的值小于后面串
*/
public int compareTo(SeqString str) {
int n = Math.min(curlen, str.curnlen) ; // 获得最短串的长度
int k = 0 ; // 循环遍历k
char[] s1 = strvalue;
char[] s2 = str.strvalue;
while(k < n) {
if(s1[k] != s2[k]) { // 处理前缀不一致
return s1[k] - s2[k];
}
k++;
}
return curlen - str.curlen; // 两个串的前缀相等
}------------------------------------------------------------------
 四、什么是模式匹配?
四、什么是模式匹配?
 4.1 概述
4.1 概述
![]() 串的查找定位操作,也称为串的模式匹配操作。
串的查找定位操作,也称为串的模式匹配操作。
![]() 主串:当前串,长度用n表示。
主串:当前串,长度用n表示。
![]() 模式串:在主串中需要寻找的子串,长度用m表示。
模式串:在主串中需要寻找的子串,长度用m表示。
![]() 模式匹配特点:
模式匹配特点:
![]() 匹配成功,返回模式串的首字母在主串中的位序号(索引号)。
匹配成功,返回模式串的首字母在主串中的位序号(索引号)。
![]() 匹配失败,返回-1
匹配失败,返回-1
![]() 模式匹配的常见算法:
模式匹配的常见算法:
![]() Brute-Force算法:蛮力算法,依次比较每一个,比较次数多,时间复杂度O(n×m)
Brute-Force算法:蛮力算法,依次比较每一个,比较次数多,时间复杂度O(n×m)
![]() KMP算法:滑动算法,比较的次数较少,时间复杂度O(n+m)
KMP算法:滑动算法,比较的次数较少,时间复杂度O(n+m)
 4.2 Brute-Force算法:分析
4.2 Brute-Force算法:分析
![]() 第一趟:运行后的结果
第一趟:运行后的结果
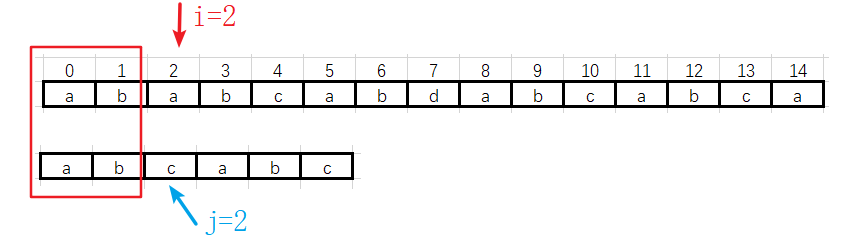
![]() 第一趟 过渡 到第二趟
第一趟 过渡 到第二趟
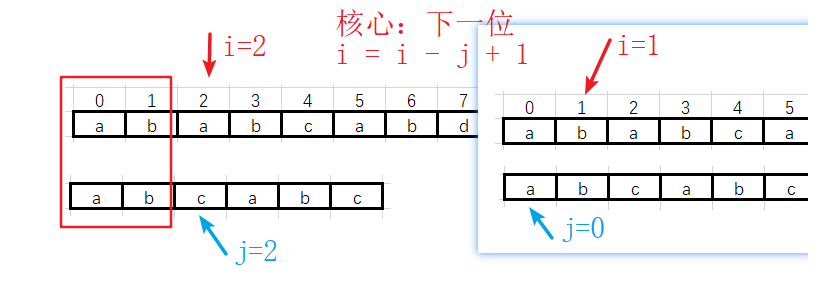
![]() 第二趟不匹配,直接 过渡 到第三趟
第二趟不匹配,直接 过渡 到第三趟
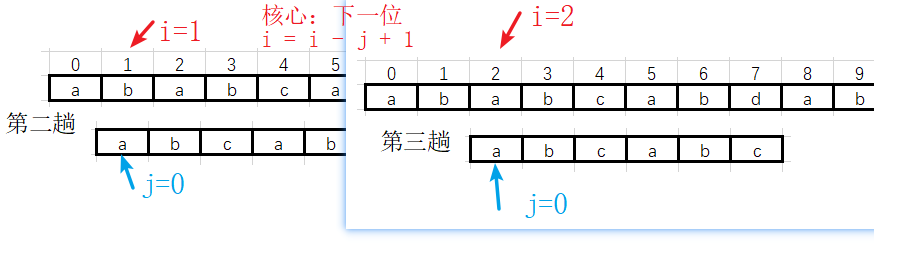
![]() 第三趟
第三趟
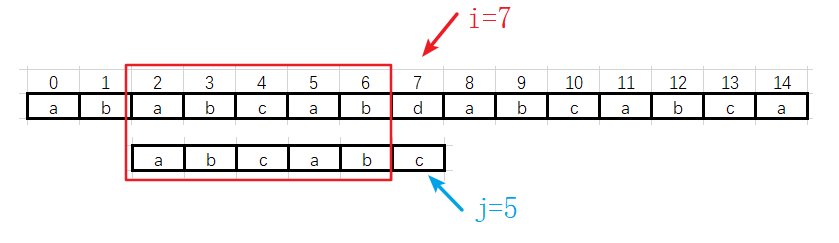
![]() 第三趟过渡到第四趟
第三趟过渡到第四趟
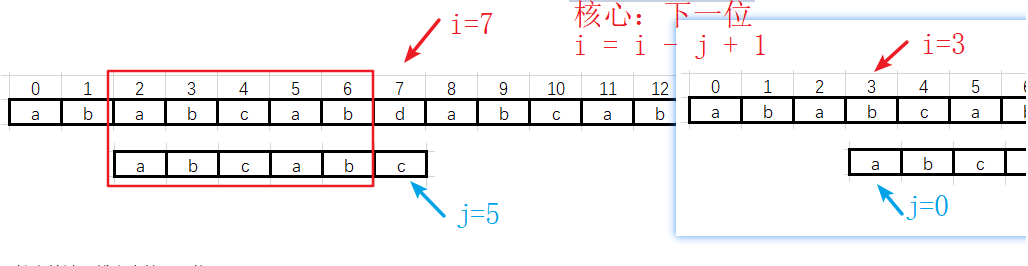
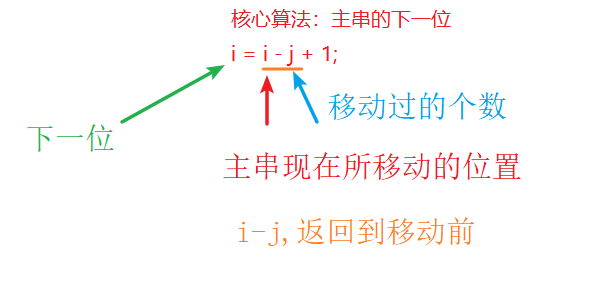
![]() 总结:核心算法(找主串的下一位)
总结:核心算法(找主串的下一位)
 4.3 Brute-Force算法:算法实现
4.3 Brute-Force算法:算法实现
/** this 主串
* @param t 模式串
* @param start 在主串中开始位置,例如:indexOf_BF("abcabc", 0)
*/
public int indexOf_BF(IString t, int start) {
// 0.1 非空校验
if(this == null || t == null) { //0.1 主串或模式串为空
return -1;
}
// 0.2 范围校验
if(t.length() == 0 || this.length() < t.length()) { //0.2模式串为空或比主串长
return -1;
}
int i = start , j = 0; // 1 声明变量
while( i<this.length() && j<t.length() ) { // 2 循环比较,主串和模式串都不能超过长度
if(this.charAt(i) == t.charAt(j)) { // 2.1 主串和模式串依次比较每一个字符
i++;
j++;
} else { // 2.2 当前趟过渡到下一趟
i = i - j + 1; // 2.3 核心算法:主串中下一字符
j = 0; // 2.4 模式串归零
}
}
// 3 处理结果
if(j >= t.length()) { //3.1 模式串已经循环完毕
return i - t.length(); //3.2 匹配成功,第一个字母的索引号
} else {
return -1; //3.3 匹配失败
}
} ![]() 注解加强版
注解加强版
/**
* this 主串
* @param t 模式串
* @param start 在主串中开始位置,例如:indexOf_BF("abcabc", 0)
* @return
*/
//Brute-Force模式匹配算法
//返回模式串t在主串中从start开始的第一次匹配位置,匹配失败时返回-1
public int indexOf_BF ( IString t , int start) {
//0.1非空校验:主串或模式串为空
if (this == null || t == null) {
return -1;
}
//0.2范围校验 : 模式串长度=0 或 主串长度比模式串长度小
if (t.length() == 0 || this.length() < t.length()) {
return -1;
}
//变量声明
//t是模式串,this表示当前主串
//当主串比模式串长时进行比较
int i = start; //i表示主串中某个子串的序号
int j = 0; // j 表示模式串当前字符的下标
int slen = this.length(); // slen 表示当前主串的长度
int tlen = t.length(); //tlen 表示当前模式串的长度
//循环条件:主串匹配的序号 < 主串的长度 ;或者 模式串当前字符下标j < 当前模式串的长度
//循环比较:主串和模式串都不能超过长度
while ((i < slen) && (j < tlen)) {
if (this.charAt(i) == t.charAt(j)) { //主串与模式串依次比较每一个字符
//相等,进行下一个字符的匹配
i++;
j++;
} else {
//当前字符不匹配,主串的下一个子串,与模式串的第一个字符继续比较;
//当前趟过滤到下一趟
i = i - j + 1; // 核心算法:i - j 回退所有已经匹配的序号,表示回到i的起始序号, +1 ,表示从下一个序号开始
j = 0; //模式串还是才第一个字符开始比较,下标归零
}
}
//如果模式串的下标索引j >= 模式串的长度,即为匹配成功
if (j >= t.length()) {
//匹配成功,返回子串序号
//返回模式串匹配成功的第一个字符在主串中的位置;
// 即当前模式串最后一个字符在主串中的位置i - 模式串的长度 = 模式串匹配成功的第一个字符所在主串中的位置
return i - tlen;
} else {
return -1;
}
}  4.4 KMP算法:动态演示
4.4 KMP算法:动态演示
![]() 核心思想:主串的指针 i 不会回退,通过
核心思想:主串的指针 i 不会回退,通过滑动模式串进行匹配。
![]() 滑动的原则:可以从最大公共前缀,直接跳 到最大公共后缀。
滑动的原则:可以从最大公共前缀,直接跳 到最大公共后缀。
![]() 思考:ababa 最大公共前后缀是?
思考:ababa 最大公共前后缀是?
![]() 最大公共前缀:==aba==ba
最大公共前缀:==aba==ba
![]() 最大公共后缀:ab==aba==
最大公共后缀:ab==aba==
![]() 动态演示
动态演示
![]() 第一趟:i 从 0 —> 2
第一趟:i 从 0 —> 2
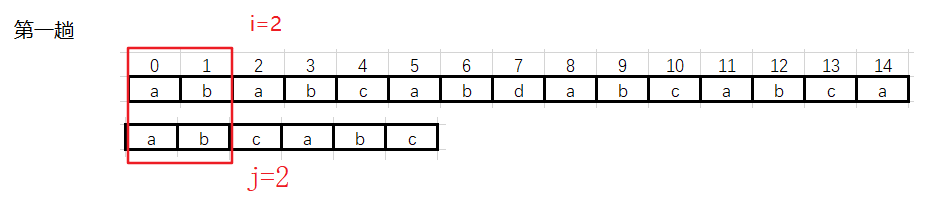
![]() 遇到不匹配的数据时,需要移动模式串,当前公共部分是“ab”,没有最大公共前后缀。模式串从头开始
遇到不匹配的数据时,需要移动模式串,当前公共部分是“ab”,没有最大公共前后缀。模式串从头开始

![]() 第二趟:i 从 2 —> 7
第二趟:i 从 2 —> 7
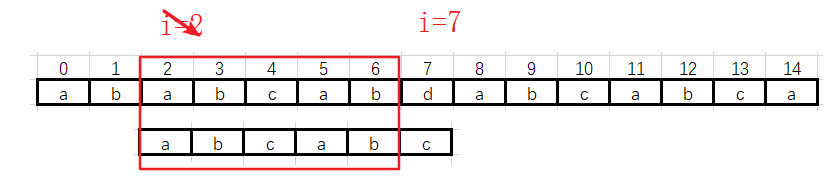
![]() 遇到不匹配的数据时,需要移动模式串,当前公共部分是“abcab”,有最大公共前后缀:
遇到不匹配的数据时,需要移动模式串,当前公共部分是“abcab”,有最大公共前后缀:

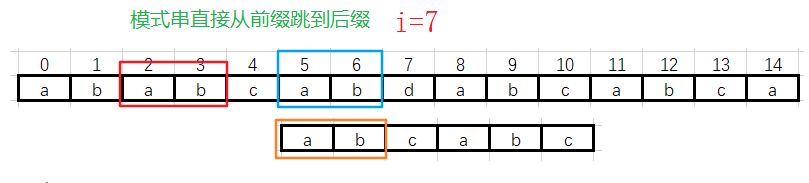
![]() 第三趟: i =7 位置数据不一致
第三趟: i =7 位置数据不一致
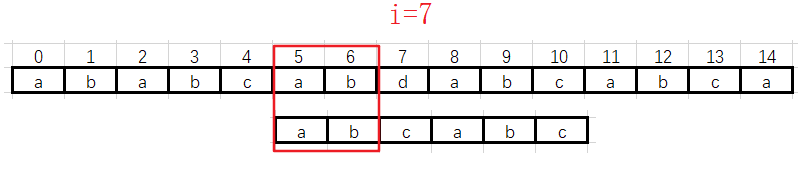
![]() 遇到不匹配的数据时,需要移动模式串,当前公共部分是“ab”,没有最大公共前后缀。模式串从头开始
遇到不匹配的数据时,需要移动模式串,当前公共部分是“ab”,没有最大公共前后缀。模式串从头开始
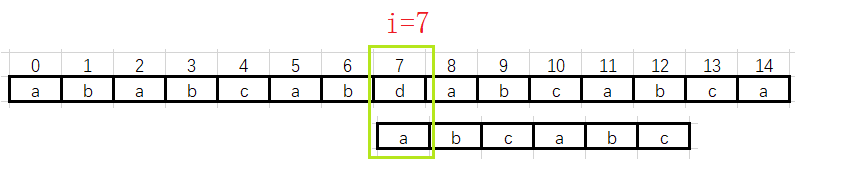
![]() 第四趟:数据不一致,i从 7—> 8
第四趟:数据不一致,i从 7—> 8
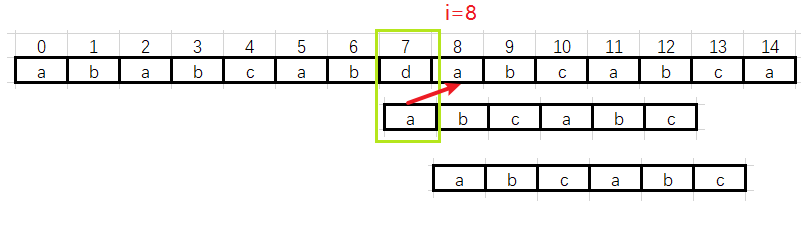
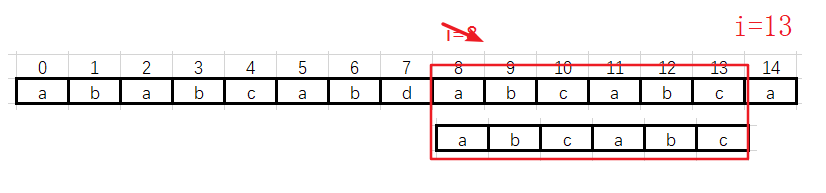
![]() 第五趟:i 从 8 —> 13,匹配成功
第五趟:i 从 8 —> 13,匹配成功
 4.5 KMP算法:求公共前后缀
4.5 KMP算法:求公共前后缀
![]() 当我们准备求公共前后缀时,主串和模式串具有相同的内容,所以只需要看模式串。
当我们准备求公共前后缀时,主串和模式串具有相同的内容,所以只需要看模式串。
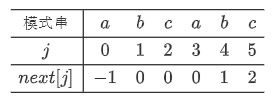
![]() 实例1:模式串:"abcabc"
实例1:模式串:"abcabc"
![]() 提前将模式进行处理(预判):将每一个字符假设不匹配时,公共前后缀提前记录下来,形成一个表格。
提前将模式进行处理(预判):将每一个字符假设不匹配时,公共前后缀提前记录下来,形成一个表格。
![]() 第一个位置:-1 (默认)
第一个位置:-1 (默认)
![]() 第二个位置:0 (默认)
第二个位置:0 (默认)
![]() 使用next数组,记录统计好的表格。
使用next数组,记录统计好的表格。
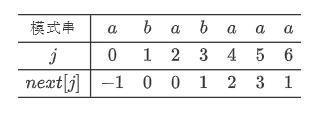
![]() 实例2:"ababaaa"
实例2:"ababaaa"
 4.6KMP算法:求公共前后缀 next数组 -- 算法演示
4.6KMP算法:求公共前后缀 next数组 -- 算法演示
![]() 实例1:模式串:"abcabc" ; 前两个值默认为-1 和 0
实例1:模式串:"abcabc" ; 前两个值默认为-1 和 0
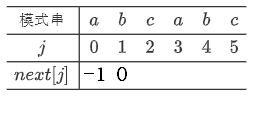
![]() 第三位的数值 :
第三位的数值 :

![]() 第四位的数值 :
第四位的数值 :

![]() 第五位的数值 :
第五位的数值 :
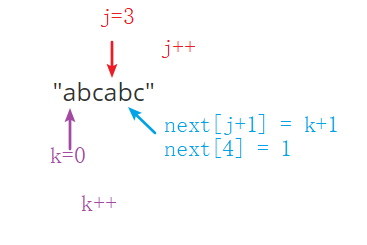
![]() 第六位的数值 :
第六位的数值 :

![]() 处理完成 :
处理完成 :
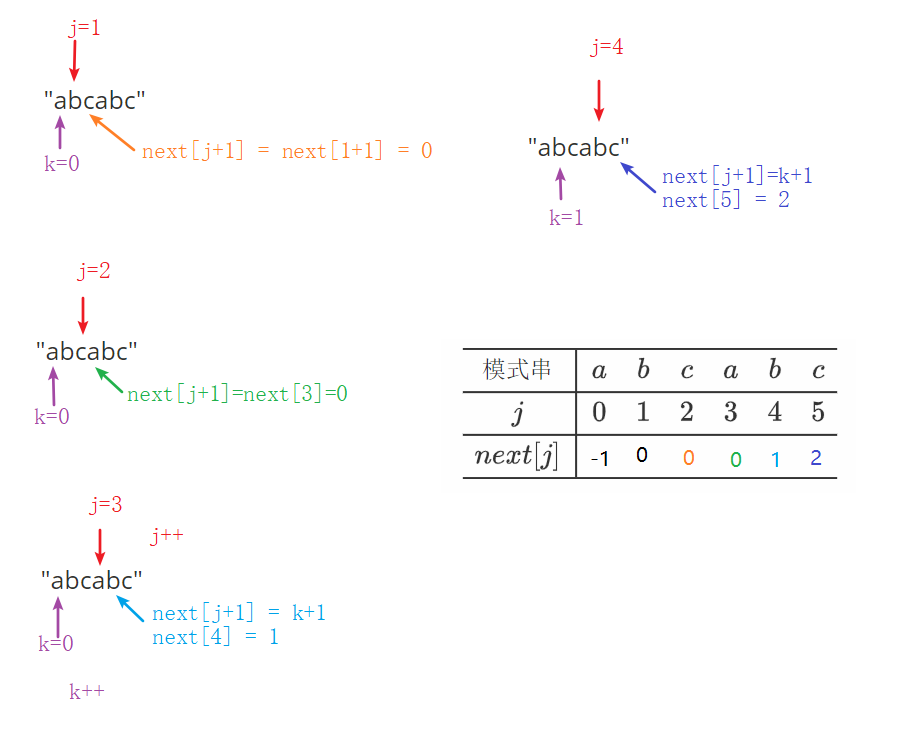
 4.7 KMP算法:求公共前后缀 next数组 -- 算法实现
4.7 KMP算法:求公共前后缀 next数组 -- 算法实现
/**
* 获得next数组
* @param T 模式串
* @return 返回next数组
*/
public int[] getNext (IString T) {
int[] next = new int[T.length()]; //创建next[] 数组,与模式串字符个数一致
int j = 1 ; //主串指针
int k = 0 ; // 模式串指针(相同字符计数器)
//2. 默认情况
next[0] = -1 ;
next[1] = 0 ;
//3. 准备比较
while (j < T.length() -1) { //比较倒数第二个字符
if (T.charAt(j) == T.charAt(k)) { //匹配,连续有字符相等
next[j+1] = k+1 ;
j++ ;
k++ ;
}else if (k == 0 ) { //失配
next[j+1] = 0 ;
j++ ;
}else { // k不是0
k = next[k] ;
}
}
//4 处理完成,返回数组
return next ;
}  4.8 KMP算法:算法实现
4.8 KMP算法:算法实现
//模式匹配的KMP算法
public int index_KMP (IString T , int start) {
int[] next = getNext(T) ; //计算模式串的next[]的函数值
int i = start ; //主串指针
int j = 0 ; //模式串指针
//对两个串从左到右进行逐个比较字符
while ( i < this.length() && j < T.length()) {
//若对应字符匹配
if (j == -1 || this.charAt(i) == T.charAt(j) ) { //j == -1 表示s[i] != T[0]
i ++ ;
j ++ ;
}else {
j = next[j] ; //模式串右移
}
}
if (j < T.length()) {
return -1 ; //匹配失败
}else {
return (i- T.length()) ; //匹配成功
}
}
如果觉得文章对您有帮助,就拿起你的小手赶紧给博主点赞、评论、收藏一下吧~~~ 赶紧动起来,让我们一起加油学习。博主会不断推出更多优质文章哟

想要了解更多吗?没时间解释了,快来点一点!
《数据结构-Java语言描述》打卡第七天 https://blog.csdn.net/zsy3757486/article/details/124001582?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第六天
https://blog.csdn.net/zsy3757486/article/details/124001582?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第六天 https://blog.csdn.net/zsy3757486/article/details/123894111?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第五天
https://blog.csdn.net/zsy3757486/article/details/123894111?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第五天 https://blog.csdn.net/zsy3757486/article/details/123862163?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第四天
https://blog.csdn.net/zsy3757486/article/details/123862163?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第四天 https://blog.csdn.net/zsy3757486/article/details/123846758?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第三天
https://blog.csdn.net/zsy3757486/article/details/123846758?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第三天 https://blog.csdn.net/zsy3757486/article/details/123810848?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第二天
https://blog.csdn.net/zsy3757486/article/details/123810848?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第二天 https://blog.csdn.net/zsy3757486/article/details/123786120?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第一天
https://blog.csdn.net/zsy3757486/article/details/123786120?spm=1001.2014.3001.5502《数据结构-Java语言描述》打卡第一天 https://blog.csdn.net/zsy3757486/article/details/123735691?spm=1001.2014.3001.5502
https://blog.csdn.net/zsy3757486/article/details/123735691?spm=1001.2014.3001.5502
最后
以上就是瘦瘦白羊最近收集整理的关于数据结构—串的概述与算法【求子串、比较、删除、插入、扩容、模式匹配】目录第三章 串与数组 第三章 串与数组 一、什么是串?二、串的存储方式有那些?三、顺序串 四、什么是模式匹配?的全部内容,更多相关数据结构—串的概述与算法【求子串、比较、删除、插入、扩容、模式匹配】目录第三章内容请搜索靠谱客的其他文章。








发表评论 取消回复