一、相关概念
1、增排序和减排序:如果排序的结果是按关键字从小到大的次序排列的,就是增排序,否则就是减排序。
2、稳定排序和不稳定排序:假设Ki=Kj(1≤i≤n,1≤j≤n,i≠j),且在排序前的序列中Ri领先于Rj(即i<j)。若在排序后的排序中Ri仍领先于Rj,即那些具有相同关键字的记录,经过排序后它们的相对次序仍然保持不变,则称这种排序方法是稳定的;反之,若Rj领先于Ri,则称所用的方法是不稳定的。
3、排序:将原有表中任意顺序的记录变成一个按关键字有序排列的过程称为排序。
4、内部排序与外部排序:在排序中,若数据表中的所有记录的排列过程都是在内存中进行的,称为内部排序。由于待排序的记录数量太多,在排序过程中不能同时把全部记录放在内存,需要不断地通过在内存和外存之间交换数据元素来完成整个排序的过程,称为外部排序。在外部排序情况下,只有部分记录进入内存,在内存中进行内部排序,待排序完成后再交换到外部存储器中加以保存。然后再将其它待排序的记录调入内存继续排序。这一过程需要反复进行,直到全部记录排出次序为止。显然,内部排序是外部排序的基础。
二、插入排序的算法思想
插入排序的基本思想是:每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子表中的适当位置,直到全部记录插入完成为止。也就是说,将待序列表分成左右两部分,左边为有序表(有序序列),右边为无序表(无序序列)。整个排序过程就是将右边无序表中的记录逐个插入到左边的有序表中,构成新的有序序列。根据不同的插入方法,插入排序算法主要包括:直接插入排序、折半插入排序、表插入排序和希尔排序等。我们学习介绍直接插入排序、折半插入排序和希尔排序。
1、直接插入排序
基本原理是顺次地从无序表中取出记录Ri(1≤i≤n),与有序表中记录的关键字逐个进行比较,找出其应该插入的位置,再将此位置及其之后的所有记录依次向后顺移一个位置,将记录Ri插入其中。
假设待排序的n个记录为{R1,R2 ,……,Rn},初始有序表为[R1],初始无序表为[R2 …Rn]。当插入第i个记录Ri(2≤i≤n)时,有序表为[R1…Ri-1],无序表为[Ri …Rn]。将关键字K i依次与Ki-1,Ki-2 ,…,K1进行比较,找出其应该插入的位置,将该位置及其以后的记录向后顺移,插入记录Ri,完成序列中第i个记录的插入排序。当完成序列中第n个记录Rn的插入后,整个序列排序完毕。
向有序表中插入记录,主要完成如下操作:
(1) 搜索插入位置。
(2) 移动插入点及其以后的记录空出插入位置。
(3) 插入记录。
假设将n个待排序的记录顺序存放在长度为n+1的数组R[1]~R[n] 中。R[0]作为辅助空间,用来暂时存储需要插入的记录,起监视哨的作用。该算法是稳定的。
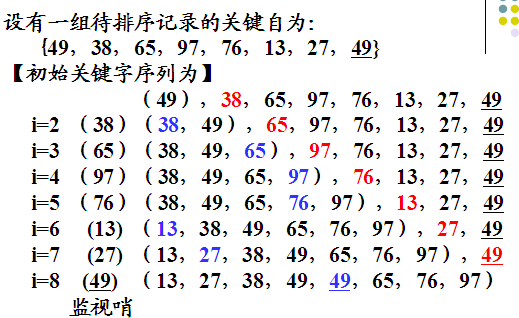
实际算法中,0单元的变化并不如上图所示。在这里只是说明0单元的作用除了辅助存储空间外,还有监视哨作用,显示当前处理的记录。
2、折半插入排序
直接插入排序的基本操作是在有序表中进行查找和插入,而在有序表中查找插入位置,可以通过折半查找的方法实现,由此进行的插入排序称之为折半插入排序。折半查找的过程是以处于有序表中间位置记录的关键字和Ki比较,经过一次比较,便可排除一半记录,把可插入的区间缩小一半,故称为折半。折半插入排序仅减少了关键字间的比较次数,但记录的移动次数不变。因此折半插入排序的时间复杂度仍为O(n2)。折半插入排序的空间复杂度与直接插入排序相同。折半插入排序也是一个稳定的排序方法。
3、希尔排序
希尔排序(shell’s sort)又称缩小增量排序(DiminishingIncrement Sort)。它是希尔(D.L.Shell)于1959年提出的插入排序的改进算法。如前所述,直接插入排序算法的时间性能取决于数据的初始特性,一般情况下,它的时间复杂度为O(n2)。但是当待排序列为正序或基本有序时,时间复杂度则为O(n)。因此,若能在一次排序前将排序序列调整为基本有序,则排序的效率就会大大提高。正是基于这样的考虑,希尔提出了改进的插入排序方法。
希尔排序的基本思想是:先将整个待排记录序列分割成若干小组(子序列),分别在组内进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。分割方法:选定一个记录的间隔值d,将所有间隔d的记录作为一组。在组内进行直接插入排序。然后缩小间隔,重新分组,再进行组内重新排序,直到间隔为1为止。
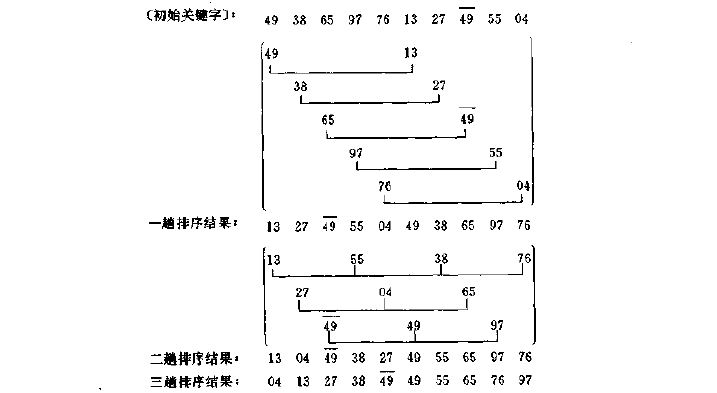

三、插入排序的C语言描述
1、直接插入排序

2、折半插入排序

3、希尔排序



四、插入排序的C语言实现
#include"stdio.h"
#include"stdlib.h"
#include"math.h"
#define OK 1
#define MAXSIZE 20
typedef intKeyType;
typedef intStatus;
typedef struct
{
KeyType key;
//InfoTypeotherinfo;
}RedType;
typedef struct
{
RedTyper[MAXSIZE+1];
int length;
}Sqlist;
voidBInsertSort(Sqlist &L)
{
int low,high;
for(inti=2;i<=L.length;++i)
{
L.r[0]=L.r[i];
low=1;
high=i-1;
while(low<=high)
{
int m;
m=(low+high)/2;
if(L.r[0].key<L.r[m].key) high=m-1;
else low=m+1;
}//while
for(int j=i-1;j>=high+1;--j)
L.r[j+1]=L.r[j];
L.r[high+1]=L.r[0];
}//for
}//BInsertSort
voidInsertSort(Sqlist &L)
{
int i,j;
for(i=2;i<=L.length;++i){
if(L.r[i].key<L.r[i-1].key)
{
L.r[0]=L.r[i];
for(j=i-1;L.r[0].key<L.r[j].key;j--)
L.r[j+1]=L.r[j];
L.r[j+1]=L.r[0];
}//if
printf("i=%d: L.[0].key:%dn",i,L.r[0].key);
}
}
voidShellInsert(Sqlist &L,int dk)
{
int i,j;
for(i=dk+1;i<=L.length;++i)
if(L.r[i].key<L.r[i-dk].key)
{
L.r[0]=L.r[i];
for(j=i-dk;j>0&&(L.r[0].key<L.r[j].key);j-=dk)
L.r[j+dk]=L.r[j];
L.r[j+dk]=L.r[0];
}//if,for
}//ShellInsertS
voidShellSort(Sqlist &L,int dlta[],int t)
{
for(intk=1;k<=t;++k)
ShellInsert(L,dlta[k]);
}
void InputL(Sqlist&L)
{
printf("inputthe length:n");
scanf("%d",&L.length);
printf("inputthe data needed to sort:n");
for(inti=1;i<=L.length;i++)
scanf("%d",&L.r[i].key);
}//InputL
voidOutputL(Sqlist &L)
{
printf("thedata after sorting is:n");
for(int i=1;i<=L.length;i++)
printf("%d ",L.r[i].key);
}
void dimish(Sqlist&L,int dlta[],int &t)
{
t=(int)floor(log10(L.length+1)/log10(2));
for(intk=1;k<=t;k++)
dlta[k]=(int)(pow(2,t-k+1)-1);
}
int main()
{
Sqlist L;
InputL(L);
intdlta[MAXSIZE],t;
//BInsertSort(L);
//InsertSort(L);
dimish(L,dlta,t);//calculatethe dlat for shellSort
ShellSort(L,dlta,t);
OutputL(L);
return OK;
}
最后
以上就是秀丽西装最近收集整理的关于20、内部排序之插入排序(直接插入、折半插入、希尔排序)的全部内容,更多相关20、内部排序之插入排序(直接插入、折半插入、希尔排序)内容请搜索靠谱客的其他文章。








发表评论 取消回复