插入排序

【基本思想】
每步将一个待排序的对象，按其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止。即边插入边排序，保证子序列中随时都是排好序的。

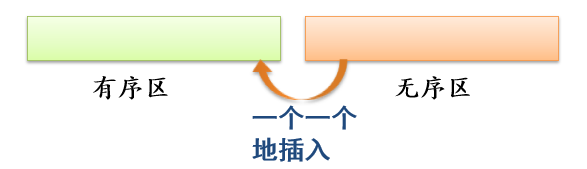
【基本操作】——有序插入
在有序序列中插入一个元素，保持序列有序，有序长度不断增加。
① 起初，a[0]是长度为1的子序列。然后，逐一将a[1]至a[n-1]插入到有序子序列中。
② 在插入a[i]前，数组a的前半段(a[0]~a[i-1])是有序段，
后半段(a[i]~a[n-1])是停留于输入次序的"无序段”。
③ 插入a[i]使a[0]~a[i-1]有序，也就是要为a[i]找到有序位置j(0≤j≤i)将a[i]插入在a[j]的位置上。

【基本步骤】
① 从第一个元素开始，该元素可以认为已经被排序，第一个元素单独成为有序区；
② 取下一个元素a[i]，从已排序的元素序列从后往前扫描；
③ 如果该元素大于a[i]，则该元素移到下一位；
④ 重复步骤③，直到找到已排序元素中小于等于a[i]的元素；
⑤ a[i]插入到该元素的后面，如果已排序所有元素都大于a[i]，则a[i]插入到第一个位置。
⑥ 重复步骤②~⑤。

插入排序的种类：
顺序法：定位插入位置——直接插入排序
二分(折半)法：定位插入位置——二分(折半)插入排序
缩小增量：多遍插入排序——希尔排序

直接插入排序

• 采用顺序查找法查找插入位置：

1、复制插入元素

x=a[i];

2、记录后移，查找插入位置

for(j=i-1;j>=0&&x<a[j];j--){
	a[j+1]=a[j];//记录后移
}

3、插入到正确位置

a[j-1]=x;

缺点：每次循环需要比较两次。

• 改进——使用"哨兵"：

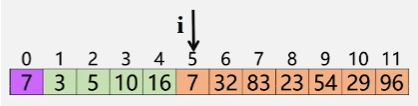
1、复制为哨兵

L.r[0]=L.r[i];

2、记录后移，查找插入位置

for(j=i-1;L.r[0].key<L.r[j].key;--j){
	L.r[j+1]=L.r[j];//记录后移
}

3、插入到正确位置

L.r[j+1]=L.r[0];

直接插入排序算法

void InsertSort(SqList &L){
	int i,j;
	for(i=2;i<=length;++i){
		if(L.r[i].key<L.r[i-1].key){//若“<”,需将L.r[i]插入有序子表
			L.r[0]=L.r[i];//复制为哨兵
			for(j=i-1;L.r[0].key<L.r[j].key;--j){
				L.r[j+1]=L.r[j];//记录后移
			}
			L.r[j+1]=L.r[0];//插入到正确位置
		}
	}
}

算法分析

时间复杂度：
① 最坏情况下(输入数据是逆有序的)——T(n)=O(n²)
② 最好情况下(关键字在记录序列中顺序有序)——T(n)=O(n)
③ 平均情况下耗时差不多是最坏情况的一半——T(n)=O(n²)

空间复杂度：
S(n)=O(1)

稳定性：
直接插入排序是一种稳定的排序方法。

原始数据越接近有序，排序速度越快。

要提高查找速度：
减少元素的比较次数
减少元素的移动次数

二分(折半)插入排序

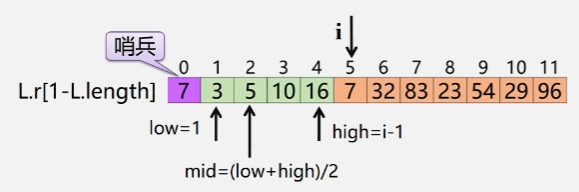
二分(折半)插入排序算法

void BInsertSort(SqList &L){
	for(i=2;i<=L.length;++i){//依次插入第2~第n个元素
		L.r[0]=L.r[i];//当前插入元素存在“哨兵”位置
		low=1;//采用二分查找法查找插入位置
		high=i-1;
		while(low<=high){
			mid=(low+high)/2;
			if(L.r[0].key<L.r[mid].key)
				high=mid-1;
			else
				low=mid+1;
		}//循环结束，high+1则为插入位置
		for(j=i-1;j>=high+1;--j){
			L.r[j+1]=L.r[j];//移动元素
		}
		L.r[high+1]=L.r[0];//插入到正确位置
	}
}

算法分析

时间复杂度为O(n²)
空间复杂度为O(1)
折半(二分)排序是一种稳定的排序方法。

① 折半查找比顺序查找快，所以折半插入排序就平均性能来说比直按插入排序要快；
② 它所需要的关键码比较次数与待排序对象序列的初始排列无关，仅依赖于对象个数。在插入第i个对象时，需要经过⌊log₂i⌋+1次关键码比较，才能确定它应插入的位置：
a. 当n较大时，总关键码比较次数比直接插入排序的最坏情况要好得多，但比其最好情况要差；
b. 在对象的初始排列已经按关键码排好序或接近有序时，直接插入排序比折半插入排序执行的关键码比较次数要少。
③ 折半插入排序的对象移动次数与直接插入排序相同，依赖于对象时初始排列
a. 减少了比较次数，但没有减少移动次数
b. 平均性能优于直接插入排序

希尔（Shell）排序

希尔排序(Shell’s Sort，又称缩小增量法Diminishing Increment Sort)是一种分组插入排序方法。

【基本思想】
先将整个待排记录序列分割成若干子序列，分别进行直接插入排序，待整个序列中的记录"基本有序”时，再对全体记录进行一次直接插入排序。
① 定义增量序列D_K：D_M>D_M-1>…>D₁=1
② 对每个D_k进行"D_k-间隔” 插入排序(k=M, M-1, …1)

例:
增量序列：D₃=5, D₂=3, D₁=1

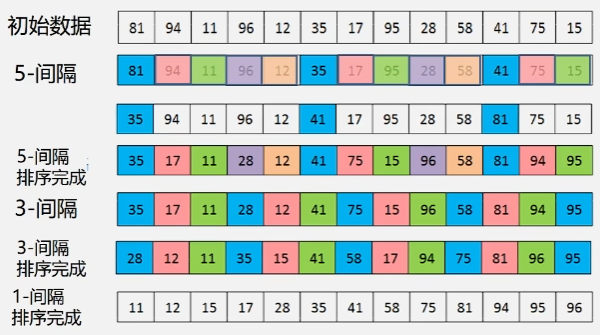
希尔排序特点：
缩小增量；多遍插入排序。
① 一次移动，移动位置较大，跳跃式地接近排序后的最终位置。
② 最后一次只需要少量移动。
③ 增量序列必须是递减的，最后一个必须是1。
④ 增量序列应该是互质的。

希尔排序算法

void ShellSort(Sqlist &L,int dlta[],int t){
//dk值依次存在dlta[t]中，按增量序列dlta[0...t-1]对顺序表L作希尔排序
	for(k=0;k<t;++k)
		ShellInsert(L,dlta[k]);//一趟增量为dlta[k]的插入排序
}

void ShellInsert(SqList &L,int dk){//对顺序表L进行一趟增量为dk的Shell排序，dk为步长因子
	for(i=dk+1;i<=L.length;++i){
		if(r[i].key<r[i-dk].key){
			r[0]=r[i];
			for(j=i-dk;j>0&&(r[0].key<r[j].key);j=j-dk){
				r[j+dk]=r[j];
			}	
			r[j+dk]=r[0];
		}
	}
}

算法分析

时间复杂度：
希尔排序的时间复杂度难以分析，是n和d的函数，一般认为约为T(n)=O(n^1.3)

空间复杂度：
S(n)=(1)

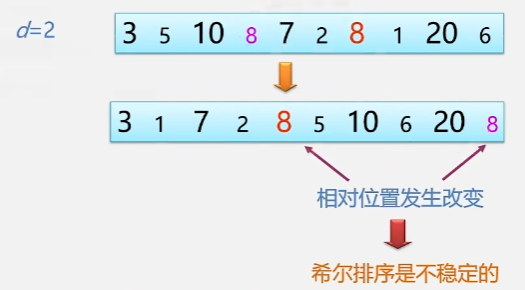
稳定性：
是一种不稳定的排序方法：

如何选择最佳d序列，目前尚未解决。
最后一个增量值必须为1，无除了1之外的公因子。
不宜在链式存储结构上实现。

最后

以上就是苹果鲜花为你收集整理的【数据结构】排序2——插入排序（直接插入排序、折半(二分)插入排序、希尔排序）插入排序的全部内容，希望文章能够帮你解决【数据结构】排序2——插入排序（直接插入排序、折半(二分)插入排序、希尔排序）插入排序所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。