排序算法(一)：插入排序(直接插入排序、希尔排序)

87 阅读 0 评论 58 点赞

我是靠谱客的博主刻苦钥匙，最近开发中收集的这篇文章主要介绍排序算法(一)：插入排序(直接插入排序、希尔排序)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、直接插入排序

1.算法思想

当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移。

2.具体算法描述

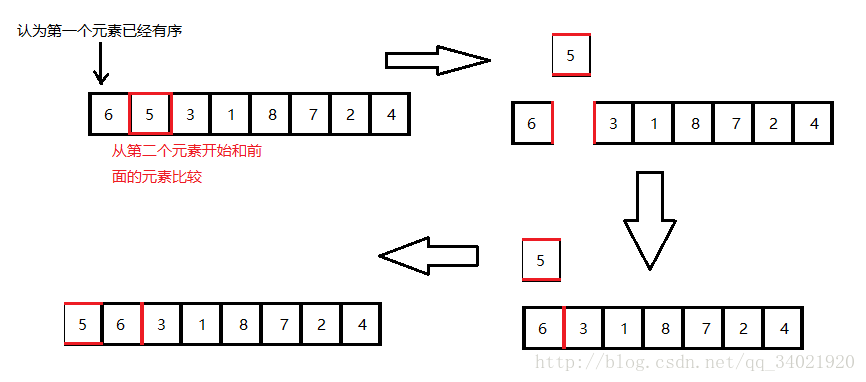
列表内容从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5

// 最差时间复杂度 ---- 最坏情况为输入序列是降序排列的,此时时间复杂度O(n^2)
// 最优时间复杂度 ---- 最好情况为输入序列是升序排列的,此时时间复杂度O(n)
// 平均时间复杂度 ---- O(n^2)
// 空间复杂度 ------ O(1)
// 稳定性 ------------ 稳定

void InsertSort(int* array, int size)
{
    for (int i = 1; i < size ; i++)
    {
        int key = array[i];
        int j = i - 1;
        while (j >= 0 && key < array[j])
        {
            array[j + 1] = array[j];
            j--;
        }
        array[j + 1] = key;
    }
}

二、插入排序的改进—->二分插入排序

对于插入排序，如果比较操作的代价比交换操作大的话，可以采用二分查找法来减少比较操作的次数，我们称为二分插入排序

// 最差时间复杂度 ---- O(n^2)
// 最优时间复杂度 ---- O(nlogn)
// 平均时间复杂度 ---- O(n^2)
// 空间复杂度 ------ O(1)
// 稳定性 ------------ 稳定

void BinaryInsertSort(int* arr, int size)
{
    for (int i = 1; i < size; i++)
    {
        int left = 0;
        int right = i - 1;
        int key = arr[i];
        while (left <= right)
        {
            int mid = left + ((right - left) >> 1);
            if (arr[mid] > key)
            {
                right = mid - 1;
            }
            else
            {
                left = mid + 1;
            }
        }
        for (int j = i - 1; j >= left; j--)
        {
            arr[j + 1] = arr[j];
        }
        arr[left] = key;
    }
}

当n较大时，二分插入排序的比较次数比直接插入排序的最差情况好得多，但比直接插入排序的最好情况要差，所当以元素初始序列已经接近升序时，直接插入排序比二分插入排序比较次数少。二分插入排序元素移动次数与直接插入排序相同，依赖于元素初始序列。

三、希尔排序

希尔排序也叫缩小增量排序，是插入排序的一种更高效的改进版本，是基于插入排序的以下两点性质而提出改进方法的：

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

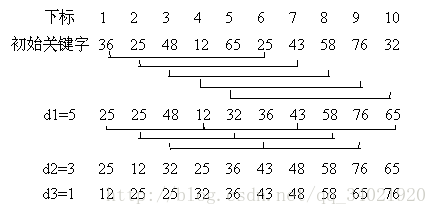
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。
　　假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n^2)的排序（冒泡排序或直接插入排序），可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据，所以小数据只需进行少数比较和交换即可到正确位置。（如下面的图）
　　这里写图片描述

// 最差时间复杂度 ---- 根据步长序列的不同而不同。已知最好的为O(n(logn)^2)
// 最优时间复杂度 ---- O(n)
// 平均时间复杂度 ---- 根据步长序列的不同而不同。
// 空间复杂度 ------ O(1)
// 稳定性 ------------ 不稳定

void ShellSort(int* arr, int size)
{
    int gap = 1;
    while (gap < size)
    {
        gap = gap * 2 + 1;
    }
    while (gap>0)
    {
        for (int i = gap; i < size; i++)
        {

            int key = arr[i];
            int j = i - gap;
            while (j >= 0 && key < arr[j])
            {
                arr[j + 1] = arr[j];
                j = j - gap;
            }
            arr[j + gap] = key;
        }
        gap = gap / 3;
    }
}