问题描述：

        给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

算法分析：

暴力解法这里就不讲解了，重点是双指针法。

方法一 ：双指针（一）

 我们从题目可以知道，数组是按升序排列的，可以有以下三种情况：

• 数组元素全都是非负数的情况下，平方之后的数据依然也是升序的；
• 数组元素全都是负数的情况下，平方之后的数据则是降序的；
• 数组元素有非负也有负数，平方之后的数据先减小后增大

这样看来，我们可以先找到数组中负数和非负数的分界线，记为flag，分界线左边为负数，非负数的右边为非负数

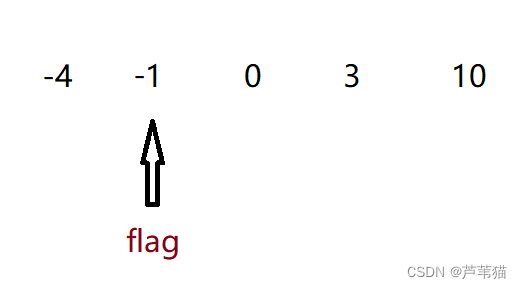
由图可知：

•  nums[0] ~ nums[flag] 全是负数
•  nums[flag+1] ~ nums[nums.size()-1] 全是非负数

当将原数组的数据平方之后，nums[0] ~ nums[flag]是单调递减的， nums[flag+1] ~ nums[nums.size()-1]是单调递增的

具体实现：

• 定义一个结果数组ans
• 定义两个指针 i 和 j 分别指向 flag 和 flag+1 的位置，即 i = flag，j = flag+1；
• 每次比较nums[i]和nums[j]的大小，选择小的数据添加到ans中
• 如果 i < 0 或者 j = nums.size()，则表示某一方移到了边界，则将另一方还未遍历的数据依次添加到ans中

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int n = nums.size();
        int flag= -1;
        //找到最后一个负数的位置
        for (int i = 0; i < n; ++i){
            if (nums[i] < 0){
                flag= i;
            } else {
                break;
            }
        }
        //结果数组
        vector<int> ans;
        //i为最后一个数组的位置，j为第一个>=0的位置
        int i = flag, j = flag+ 1;
        while (i >= 0 || j < n){
            //此时小于0的数已经全部放进结果集，只需看j的
            if (i < 0){
                ans.push_back(nums[j] * nums[j]);
                ++j;
            }
            //此时j那边的数已经全部遍历完
            else if (j == n){
                ans.push_back(nums[i] * nums[i]);
                --i;
            }
            //i的平方小于j的平方
            else if(nums[i] * nums[i] < nums[j] * nums[j]){
                ans.push_back(nums[i] * nums[i]);
                --i;
            }
            //i的平方大于j的平方
            else{
                ans.push_back(nums[j] * nums[j]);
                ++j;
            }
        }
        return ans;
    }
};
 

复杂度分析：

时间复杂度：O(n)，其中n是数组nums 的长度。

空间复杂度：O(1)，除了存储答案的数组以外，我们只需要维护常量空间。

方法二 ：双指针(二）

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int n = nums.size();
        vector<int> ans(n);
        int i = 0;//数组的起始位置
        int j = n - 1;//数组的终止位置
        int k = n - 1;//ans数组插入数据的位置
        while(i<=j)
        {
            if(nums[i]*nums[i] > nums[j]*nums[j])
            {
                ans[k] = nums[i]*nums[i];
                i++;
            }
            else
            {
                ans[k] = nums[j]*nums[j];
                j--;
            }
            --k;
        }
        return ans;
    }
};

最后

以上就是等待镜子为你收集整理的LeetCode——977.有序数组的平方（C++）问题描述：算法分析：的全部内容，希望文章能够帮你解决LeetCode——977.有序数组的平方（C++）问题描述：算法分析：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。