【课程笔记01】数字信号处理

自用，个人课程笔记

目录

• • • 周期信号的判断
    • 功率信号和能量信号
    • 时不变特性
    • 线性
    • 稳定系统
    • 狄利克雷条件
    • 傅里叶变换FT（Fourier Transform）
  • 连续时间复指数信号等
  • • s平面和z平面的关系
    • Sa函数
    • 频谱
    • 常见傅里叶变换求解
    • 留数定理
    • 理想低通滤波器不可实现的原因
  • 随机信号处理
  • • 截图
    • • Laplace
      • z变换

Fourier变换是虚轴上的Laplace变换
$s=\sigma +j\omega$
$z=e^{sT}$

周期信号的判断

1. 周期信号与周期信号的叠加不一定是周期信号
2. $sin(t)$为周期信号，周期为2$\pi$
   $sin(n)$不为周期信号，找不到N满足$sin(n+mN)=sin(n)$，m为整数
   $sin(\frac{\pi n}{4})$是周期信号，$sin(\frac{\pi }{4}(n+8m))=sin(n)$。
   对正弦函数的采样周期需要是$2\pi$的整数倍（正弦序列不一定是周期信号）

功率信号和能量信号

能量有限信号：$E={\int }_{-\infty }^{+\infty }|x(t){|}^{2}dt$
能量有限信号：$P={\lim }_{T\to \infty }\frac{1}{T}{\int }_{-T/2}^{T/2}|x(t){|}^{2}dt$
斜坡信号既不是功率有限信号也不是能量有限信号

时不变特性

• 例题：$y(t)=x(-t)$；系统的作用为对输入进行翻转

1. 输入时移$x(t-t_0)$，系统输出为$x(-t-t_0)$ ，即$y(t+t_0)$，系统只对t进行操作
2. 而输出时移应为$y(t-t_0)=x(-(t-t_0))=x)(-t+t_0)$
   从而不为时不变系统，并非数学上的变量替换

• 例题 $y(n)=nx(n)$也不为时不变系统。
  因为输入$x(n-n_0)$时，输出为$nx(n-n_0$，不等于$y(n-n_0)$

• 连续时不变系统可以用常系数微分方程表示

• 离散时不变系统可以用常系数差分方程表示

线性

• 齐次（倍乘）
• 可加
• 可分解性（零输入和零状态）
  • 零输入线性？将$x(t)=0$，则剩余的$y(t)$为0输入响应
    $y(t)=2x(t)+3$，零输入为$y(t{)}_{zeroinput}=3$，并非线性
  • 零状态线性？ 减去零输入
    $y(t{)}_{zerostate}=2x(t)$，为线性的值

稳定系统

• 有界输入对应有界输出
• 充要条件：单位冲激响应绝对可积
  ${\int }_{-\infty }^{+\infty }|h(t)|dt<-\infty$
• 因果系统稳定的条件：极点全部位于左半平面（z平面单位圆内部）

系统的分类：因时线连记稳。。。（因为时间线连记忆都稳定了）
因果与非因果；时不变与时变；线性与非线性；连续与离散；记忆与非记忆；稳定与不稳定

狄利克雷条件

狄利克雷（1805～1859），德国数学家。

是一个信号存在傅里叶变换的充分不必要条件。
狄利克雷条件括三方面：

1. 在一周期内，连续或只有有限个第一类间断点；
   可去间断点和跳跃间断点属于第一类间断点。（左极限和右极限都存在）
2. 在一周期内，极大值和极小值的数目应是有限个；
3. 在一周期内，信号是绝对可积的。

其他科学家

1. 奈奎斯特（1889-1976），美国物理学家。1917年获得耶鲁大学工学博士学位。曾在美国AT&T公司与贝尔实验室任职。

傅里叶变换FT（Fourier Transform）

• $t$连续对应$\omega$无穷
  $X(e^{j\Omega })={\int }_{-\infty }^{+\infty }f(t)e^{-j\Omega t}dt$

连续时间复指数信号等

1. 复指数信号：$e^{st}$
   $s=\sigma +j\omega$

2. 阶跃信号（单边特性）
   $u(t)=1,t\ge 0,else,u(t)=0$
   符号函数： $sgn(t)=1(-1),t>0(<0)$
   $sgn(t)=u(t)-u(-t)=2u(t)-1$

3. 冲激函数 $\delta (t)=0$

• 筛选性质：$x(t)\delta (t)=x(0)\delta (t)$（x(0)为面积）

• 取样性质：${\int }_{-\infty }^{+\infty }x(t)\delta (t)=x(0)$

• 展缩性质：$\delta (at+b)=\frac{1}{|a|}\delta (t+b/a)$：冲激信号是偶函数

  • 证明： 根据冲激函数的取样性质进行
  • $${\int }_{-\infty }^{+\infty }\delta (at+b)\varphi (t)dt\stackrel{at+b=P,a>0}{⟶}{\int }_{-\infty }^{+\infty }\delta (P)\varphi (\frac{P-b}{a})d(\frac{P-b}{a})={\int }_{-\infty }^{+\infty }\frac{1}{a}\delta (P)\varphi (\frac{P-b}{a})dP=\frac{1}{a}\varphi (\frac{-b}{a})$$
    最后一个等式中，可以看成$\delta (P+0)$在与$\varphi$函数进行取样，从而零$\varphi$中的P等于0
    小于0时同理，积分上下限需要改变符号。因此a有绝对值

• 冲激信号微分积分性质：

  1. ${\int }_{-\infty }^t\delta (\tau )d\tau =u(t)$
  2. ${\int }_{-\infty }^{t}u(\tau )d\tau =tu(t)$（斜坡信号）
  3. $\frac{d\delta (t)}{dt}={\delta }^{{}^{\prime }}(t)$（冲激偶函数）

• 奇异信号：所有从单位冲激信号导出的这些信号统称为奇异信号

s平面和z平面的关系

• s平面：$s=\sigma +j\omega$，$x(t)=e^{st}=e^{(\sigma +j\omega )t}=e^{\sigma t}{e}^{j\omega t}$
• s平面为直角坐标系，横坐标$\sigma$，纵坐标$j\omega$
• z平面：$z=r{e}^{j\Omega }$，$x(n)=z^n$
• z平面为极坐标系，长度r，角度$\Omega$

1. 令t=nT对x(t)进行采样，$x(t)=e^{\sigma nT}{e}^{j\omega nT}$
2. 确定采样频率，$T=\frac{2\pi }{{\omega }_s}$
3. 则$x(n)=e^{\sigma n\frac{2\pi }{{\omega }_s}}{e}^{j\omega n\frac{2\pi }{{\omega }_s}}$
4. s域变量 $\sigma$和$\omega$，z域的变量r，$\Omega$。
   • $r=e^{\sigma n\frac{2\pi }{{\omega }_s}}$， $e^{jn\omega \frac{2\pi }{{\omega }_s}}$
   • 角度为$n\omega \frac{2\pi }{{\omega }_s}$
5. 1. 对于s左半平面，$\sigma <0$时，$x(t)=e^{st}$衰减，x(n)的r<1，即在z平面单位圆内部，此时如果让$n\omega \frac{2\pi }{{\omega }_s}$为（0，$2\pi$），则$\omega \in (0,w_s)$时，完整对应z平面的角度，$\omega$再向上或者向下平移也对应的是z平面单位圆内部，s左半平面对应单位圆内部，为多对1的关系。
   2. 对于s右半平面，对应单位圆外部
   3. s平面的$j\omega$ 轴对应z平面的长度为1，即对应单位圆。例如s的原点，$\omega =0$ ，z平面角度为0，$\sigma =0$，长度为1，从而原点对应z平面（0，1）的位置在单位圆上。
   4. s平面的实轴，$\omega =0$，对应的是z平面的角度为0，$\sigma 不一定时$对应长度不一定，从而实轴为z平面的横坐标的右半部分

Sa函数

$Sa(t)=\frac{sin(t)}{t}$

1. 偶函数
2. t=k$\pi$时，sa(t)=0
3. t=0时，sa(t)=1
4. 负无穷到正无穷上积分为$\pi$

门函数的频谱为Sa函数

频谱

1. 偶函数的频谱是偶函数，奇函数的频谱是奇函数

   • 证明：
   • 偶函数：$x(t)=x(-t)$
   • 对于x(t)：$X(j\omega )={\int }_{-\infty }^{+\infty }x(t)e^{-j\omega t}dt$
   • 对于x(-t)：$X(-j\omega )={\int }_{-\infty }^{+\infty }x(t)e^{j\omega t}dt$
   • 变量替换：$t=-\tau$
   • 从而$X(-j\omega )={\int }_{+\infty }^{-\infty }x(-\tau )e^{j\omega (-\tau )}d(-\tau )$
   • $⟹$ $X(-j\omega )={\int }_{-\infty }^{+\infty }x(\tau )e^{-j\omega \tau }d\tau =X(j\omega )$从而得证频谱为偶函数
     
     
2. • 实信号（共轭相等）：$x(t)=x^{\ast }(t)$ 有$X(j\omega )=X^{\ast }(-j\omega )$ 先取负，再取共轭
   • 证明：
   • 求$x^{\ast }(t)$的频谱，如果等于$X^{\ast }(-j\omega )$，则得到证明
   • ${\int }_{-\infty }^{+\infty }{x}^{\ast }(t)e^{-j\omega t}dt⟹[{\int }_{-\infty }^{+\infty }x(t)e^{j\omega t}dt{]}^{\ast }=X^{\ast }(-j\omega )$
   • 证明结束
     
     

3. 实信号：

   • 模值为偶函数，角度为奇函数（根据$X(j\omega )=X^{\ast }(-j\omega )$证明）
   • $X(j\omega )=Re[X(j\omega )]+jIm[X(j\omega )]$
   • $X^{\ast }(-j\omega )=Re[X(-j\omega )]-jIm[X(-j\omega )]$
   • 以上两式相等，实部等于实部，虚部等于虚部
   • 模值=$\sqrt{R{e}^2+I{m}^2}$为偶函数
   • 角度$arctan(\frac{Im}{Re})$从而为奇函数

4. 如果既是实信号$X(j\omega )=X^{\ast }(-j\omega )$，
   又是偶函数，频谱为偶函数$X(j\omega )=X(-j\omega )$

   • 实偶函数$X^{\ast }(-j\omega )=X(-j\omega )$，因此实偶函数虚部为0，从而角度也为0
   • 实偶函数频谱为实偶函数
   • 实奇函数$X\ast (-j\omega )=-X(-j\omega )$，因此虚部为0，从而角度为$\pi /2$
   • 实奇函数频谱为虚奇函数

5. 对称性质（定义本质）：或者写为：$2\pi x(-\omega )=X(jt)$，$x(t)\leftrightarrow X(\omega )⟹X(t)=2\pi x(-\omega )$

   • 证明：$2\pi x(-\omega )=X(jt)$
   • 从$x(-\omega )$下手：$x(-t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(j\omega )e^{-jwt}dw$
   • $t=\omega$: $x(-\omega )=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(jt)e^{-jwt}dt$ （这里是为什么？）
   • 或许可以将$X(j\omega )d\omega$看成是幅值，$e^{-j\omega t}$看成角度，实际上$\omega$和$t$等价？

6. 时频展缩特性$x(at)\leftrightarrow \frac{1}{|a|}X(j\omega /a)$，可以参考$\delta (at+b)=\frac{1}{|a|}\delta (t+b/a)$

   • 相当于时域越宽，则频域越窄
   • $x(-t)=X(-j\omega )$

7. 时移特性$x(t+t0)\leftrightarrow X(j\omega )e^{j\omega t_0}$ （定义与变量替换证明）

   • 只是影响了相位
   • $x(t+b)->X(j\omega )e^{j\omega b}$
   • $x(at+b)->\frac{1}{|a|}X(j\omega /a)e^{jwb/a}$

8. 频移$x(t)e^{j{w}_{0}t}\leftrightarrow X(j(w-w_0))$

9. 微分特性 $x^{n^{\prime }}(t)=(jw{)}^{n}X(jw)$定义求解

10. 频域微分特性$tx(t)\leftrightarrow jdX(jw)/dw$

常见傅里叶变换求解

1. $\delta (t)\leftrightarrow 1$
   ${\int }_{}^{}\delta (t)e^{-j\omega t}=e^{-jw0}=1$
2. $1\leftrightarrow 2\pi delta(w)$，根据对称性质求解 $2\pi \delta (-\omega )=2\pi \delta (\omega )$
   $2\pi x(-\omega )\leftrightarrow X(t)$
   $2\pi \delta (-\omega )\leftrightarrow 1$
3. $e^{-at}u(t)$
   • $X(j\omega )={\int }_0^{+\infty }{e}^{-at}{e}^{-j\omega t}dt=\frac{e^{-(a+j\omega )t}}{-(a+j\omega )}{|}_0^{+\infty }=\frac{1}{a+j\omega }$
4. $sgn(t)\leftrightarrow 2/(j\omega )$ （实奇函数对应虚奇频谱，化为u(t)相减的形式求解）
   • $sgn(t)={\lim }_{a->0}[e^{-at}u(t)-e^{at}u(-t)]$
5. $e^{j{w}_{0}t}$，根据对称与频移特性求解
   • $1\leftrightarrow 2\pi \delta (w)$
   • 频移：$e^{j{w}_{0}t}=2\pi \delta (w-w_0)$
6. $cos(w_{0}t)$
   • 欧拉公式与$e^{j{w}_{0}t}$求解
   • $cos(w_{0}t)=1/2(e^{j{w}_{0}t}+e^{-j{w}_{0}t})$
   • $cos(w_{0}t)=\pi \delta (w-w_0)+\pi \delta (w+w_0)$
7. $sin(w_{0}t)$
   • $j\pi \delta (w+w_0)-j\pi \delta (w-w_0)$
8. $u(t)=1/2+1/2sgn(t)$
   • $u(t)\leftrightarrow \pi \delta (w)+1/j$

留数定理

• 有向围线上的积分等于围线内所有极点留数之和再乘以$2\pi$。

理想低通滤波器不可实现的原因

1. 写出LPF的$H(j\omega )$
2. 写出LPF的时域上的公式h(t)（门函数与Sa函数相对应）
3. h(t)与$\delta (t)$相比较发生失真（原因是$\delta (t)$的频域分量并非所有都被通过）
4. h(t)为非因果信号，不可实现

• 佩利-维利准则：
• ${\int }_{-\infty }^{+\infty }\frac{|ln|H(j\omega )||}{1+{\omega }^2}d\omega <-\infty$
• 即$H(j\omega )$若有一段为0，则不可实现

随机信号处理

1. 自相关函数
2. 已知功率谱密度，求解最小相位表示，并表示自相关函数（正则谱分解 ）
3. 功率谱密度为实函数：（证明共轭相等）$R(j\omega )=R^{\ast }(j\omega )$

• 证明：从自相关函数着手
  • 自相关函数（偶对称的）：$r_x(m)=E[x(n+m)x^{\ast }(n)]⟹(提出共轭)E^{\ast }[x^{\ast }(n+m)x(n)]⟹(n=n-m)⟹E^{\ast }[x^{\ast }(n+m-m)x(n-m)]=E^{\ast }[x^{\ast }(n)x(n-m)]=r^{\ast }(-m)$
    • 偶对偶，奇对奇（Fourier）
    • 实对取负取共轭（Fourier）(自相关函数也是)
    • 实偶对实偶，实奇对虚奇（Fourier）
• $FT(r^{\ast }(-m))=R^{\ast }(e^{j\omega })$

截图

Laplace

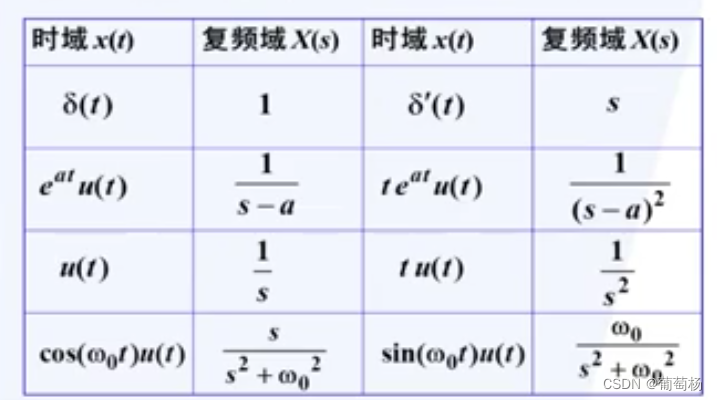
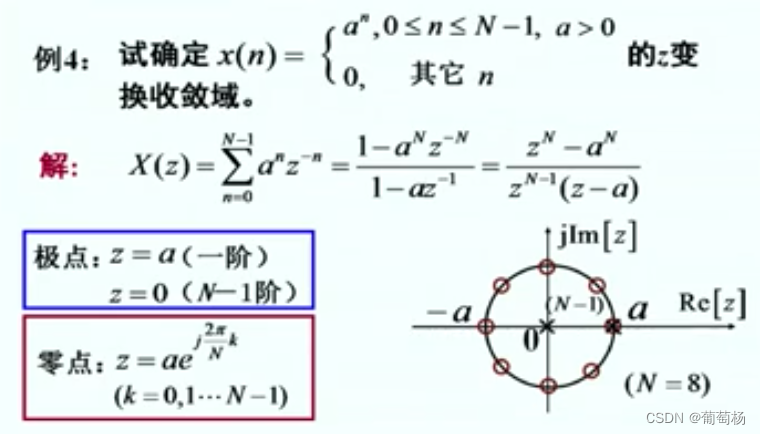
z变换

1. 有限长离散时间信号z变换的收敛域是整个有限z平面。（可能不包括z=0【因果有限长序列】，或者$|z|=-\infty$【反因果】）因果系统，z平面收敛域应包含无穷
   

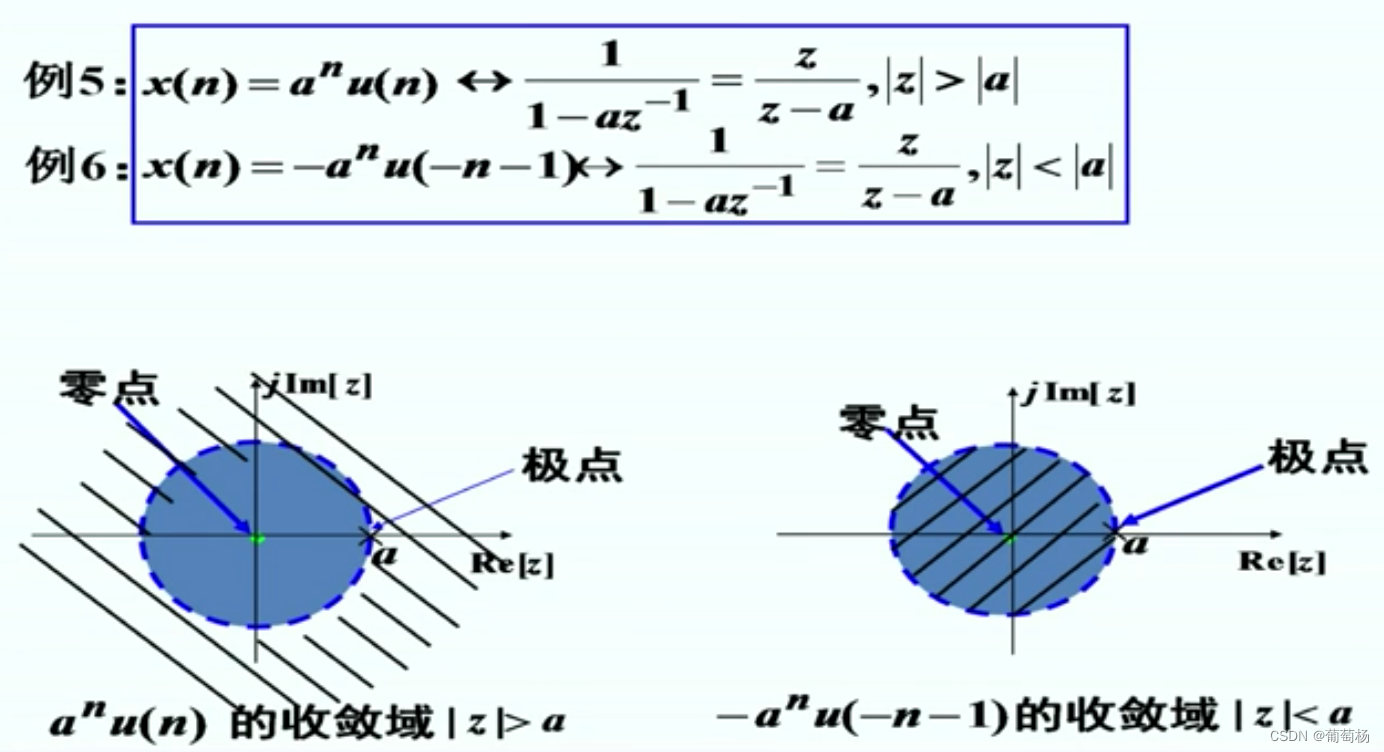
最后

以上就是谦让铃铛为你收集整理的【课程笔记01】数字信号处理的全部内容，希望文章能够帮你解决【课程笔记01】数字信号处理所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。