频谱分析是进行信号分析的基础,这里我们采用三种简单的样本(正弦波、方波、噪声)进行频谱分析。我们用MATLAB和Python同时仿真,验证其正确性。具体操作如下:
1、用MATLAB生成一个样本并保存为WAV文件,并用MATLAB画出波形和频谱图。
2、用Python读取对应的WAV文件,并画出波形和频谱图。
1、正弦波的波形和频谱
这里我们生成一个简单的正弦波: y=sin(2∗π∗200∗t) y = s i n ( 2 ∗ π ∗ 200 ∗ t ) ,正弦波的频率为200Hz。
1.1 基于MATLAB的波形和频谱
具体代码如下:
Df=5; %频率间隔
fs = 8000; %采样频率
T = 1/fs; %采样周期
N=fs/Df; %序列点数
time = (N-1)./fs; %第一个声音片段的总时长
t=0:T:(N-1)./fs;
y = sin(2*pi*200*t); %生成第一个声音片段。
freq=0:Df:(N-1)*Df; %计算频率段
Y=fft(y,N); %用FFT计算频谱
filename = ('sinwave.wav'); %给文件取名
audiowrite(filename,y,fs) %存储.wav音频文件,在这里文件名为sinwave.wav
subplot(211);
plot(t,y);
title('正弦波波形');
subplot(212);
plot(freq-fs/2,abs(fftshift(Y))); %将零频率移动到FFT中心
xlabel('频率 Hz');ylabel('幅度谱'); %并作出幅度频谱
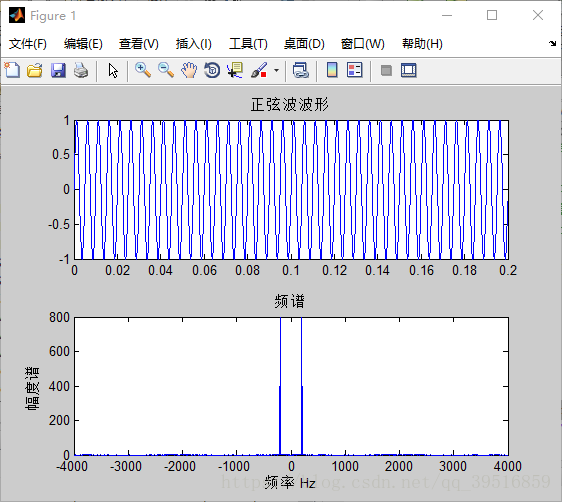
title('频谱');实现结果如下:
1.2 基于Python的波形和频谱
import wave
import numpy as np
import pylab as plt
from scipy.fftpack import fft,ifft
#打开wav文件 ,open返回一个的是一个Wave_read类的实例,通过调用它的方法读取WAV 文件的格式和数据。
f = wave.open(r".sinwave.wav","rb")
#读取格式信息
#一次性返回所有的WAV文件的格式信息,它返回的是一个组元(tuple):声道数, 量化位数(byte单位), 采
#样频率, 采样点数, 压缩类型, 压缩类型的描述。wave模块只支持非压缩的数据,因此可以忽略最后两个信息
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
#读取波形数据
#读取声音数据,传递一个参数指定需要读取的长度(以取样点为单位)
str_data = f.readframes(nframes)
f.close()
#将波形数据转换成数组
#需要根据声道数和量化单位,将读取的二进制数据转换为一个可以计算的数组
wave_data = np.fromstring(str_data,dtype=np.int16)
wave_data = wave_data*1.0/(max(abs(wave_data)))#wave幅值归一化
#通过取样点数和取样频率计算出每个取样的时间。
time=np.arange(0,nframes)/framerate
# 从波形数据中取样nframes个点进行运算
xs = wave_data [:nframes]
# xf=np.fft.rfft(xs)
# #于是可以通过下面的np.linspace计算出返回值中每个下标对应的真正的频率:
# freqs=np.linspace(0,framerate/2, nframes/2+1)
xf= np.fft.fft(xs)
freqs = np.fft.fftfreq(nframes,1.0/framerate)
print(params)
plt.subplot(211)
plt.plot(time[:nframes], xs)
plt.xlabel("time(s)")
plt.title('Original wave')
plt.subplot(212)
plt.plot(freqs,np.abs(xf),'r') #显示原始信号的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)')
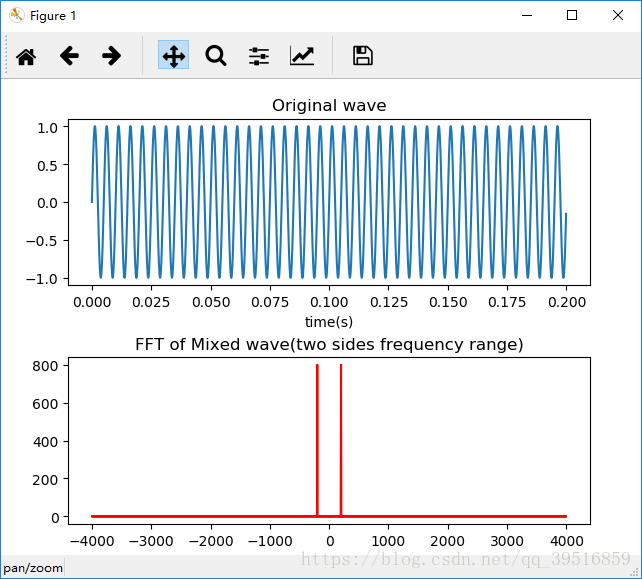
plt.show()实现结果如下:
1.3 分析
由1.1和1.2中基于MATLAB和Python的波形及频谱图可以看出两种环境下的仿真结果相同,正弦波的波形频率为200Hz,幅值为1。频谱图中可以看出正弦波的频率在 ±200Hz ± 200 H z 附近。与开始假设的正弦波一致。
2、psk的波形和频谱
这里我们先生成一个周期为0.04,幅值为1,占空比为50的方波。然后对方波进行psk调制得到psk信号。仿真分析psk信号的频谱。
2.1 基于MATLAB的波形和频谱
具体代码如下:
Df=5; %频率间隔
fs = 8000; %采样频率
T = 1/fs; %采样周期
N=fs/Df; %序列点数
time = (N-1)./fs; %第一个声音片段的总时长
t=0:T:time;
y=square(2*pi*25*t,50) %产生一个周期为0.04,占空比为50%的方波。
car=sin(2*pi*100*t); %载波
psk=y.*car; %载波调制(相乘器)
freq=0:Df:(N-1)*Df; %计算频率段
Y=fft(y,N); %用FFT计算频谱
filename = ('psk.wav'); %给文件取名
audiowrite(filename,psk,fs) %存储.wav音频文件,在这里文件名为sinwave.wav
subplot(311);
plot(t,y);
axis([0 0.2 -2 2]);
title('方波波形');
subplot(312);
plot(t,psk);
axis([0 0.2 -2 2]);
title('2PSK信号');
subplot(313);
plot(freq-fs/2,abs(fftshift(Y))); %将零频率移动到FFT中心
xlabel('频率 Hz');ylabel('幅度谱'); % 并作出幅度频谱
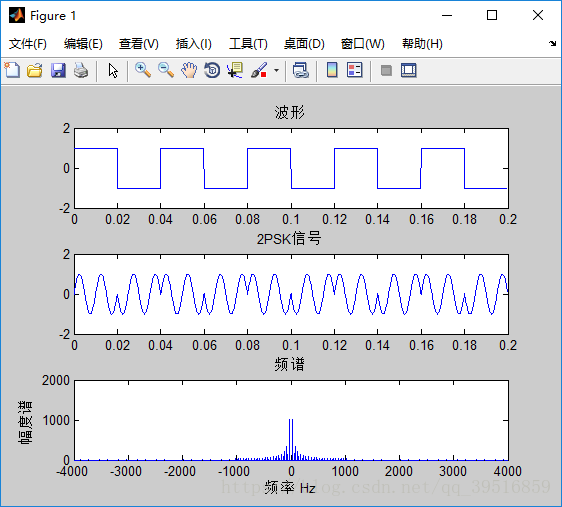
title('频谱');实现结果如下:
2.2 基于Python的波形和频谱
具体代码如下:
import wave
import numpy as np
import pylab as plt
from scipy.fftpack import fft,ifft
#打开wav文件 ,open返回一个的是一个Wave_read类的实例,通过调用它的方法读取WAV 文件的格式和数据。
f = wave.open(r".psk.wav","rb")
#读取格式信息
#一次性返回所有的WAV文件的格式信息,它返回的是一个组元(tuple):声道数, 量化位数(byte单位), 采
#样频率, 采样点数, 压缩类型, 压缩类型的描述。wave模块只支持非压缩的数据,因此可以忽略最后两个信息
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
#读取波形数据
#读取声音数据,传递一个参数指定需要读取的长度(以取样点为单位)
str_data = f.readframes(nframes)
f.close()
#将波形数据转换成数组
#需要根据声道数和量化单位,将读取的二进制数据转换为一个可以计算的数组
wave_data = np.fromstring(str_data,dtype=np.int16)
wave_data = wave_data*1.0/(max(abs(wave_data)))#wave幅值归一化
#通过取样点数和取样频率计算出每个取样的时间。
time=np.arange(0,nframes)/framerate
# 从波形数据中取样fft_size个点进行运算
xs = wave_data [:nframes]
# xf=np.fft.rfft(xs)
#于是可以通过下面的np.linspace计算出返回值中每个下标对应的真正的频率:
# freqs=np.linspace(0,framerate/2, nframes/2+1)
xf= np.fft.fft(xs)
freqs = np.fft.fftfreq(nframes,1.0/framerate)
print(params)
plt.subplot(211)
plt.plot(time[:nframes], xs)
plt.xlabel("time(s)")
plt.title('Original wave')
plt.subplot(212)
plt.plot(freqs,np.abs(xf),'r') #显示原始信号的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)')
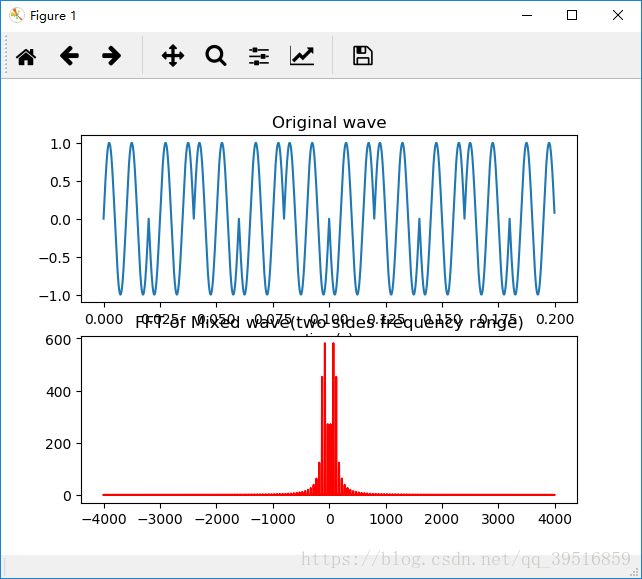
plt.show()实现结果如下:
2.3 分析
由2.1和2.2中基于MATLAB和Python的波形及频谱图可以看出两种环境下的仿真结果相同,方波的波形周期为0.25,幅值为1。对方波进行psk调制得到了正确的调相信号。
最后
以上就是美好灰狼最近收集整理的关于基于MATLAB和Python的频谱分析的全部内容,更多相关基于MATLAB和Python内容请搜索靠谱客的其他文章。








发表评论 取消回复