Python_FFT

简单记录一下，免得到时候又去四处找代码。

这部分代码是我朋友写的，在这推荐一下他的博客：

叮叮当当sunny

很强的一位小伙伴，感兴趣的朋友可以看看。

上代码：

import numpy as np
from scipy.fftpack import fft
def FFT(data,Fs):
    n=len(data)
    if n%2!=0:
        n-=1
        # data=data[range(0,n)]  #由于要进行取半处理，所以将n与2取余
        data.pop()
    Y=fft(data)    #快速傅里叶变换
    Fre=np.linspace(0,n-1,n)*Fs/n  #linspace(start,stop,number)
    Fre=Fre[range(0,int(n/2))]
    Amp=np.abs(Y[range(0,int(n/2))])
    Amp=Amp/(n/2)
    Amp[0]=Amp[0]/2
    Amp[-1]=Amp[-1]/2  
    return Fre, Amp

代码注释比较少哈，我加点文字解释说明一下：

第一个参数就是傅里叶分析的波形函数采样的值，第二个参数是单位时间采样点数，是指一秒钟的时间采几个点的数据。

举例说明：

两个周期我给了100个点，所以一个周期就是50个点，假定一个周期有10秒，那么10秒对应的是50个点，1秒就是5个点，一个周期10秒，基频就是0.1，所以如果只分析谐波的话，就是0.3，0.5，0.7之类的。这样对应的基波、三次谐波、五次谐波就都能出来了。

把例子及绘图的代码一并附上：

func1=func[:76]   #取两个周期的点
F,A=FFT(func1,38)
plt.bar(F,A,width=0.4)
x=range(0,15,1)
plt.xlim(0,15)
plt.xticks(x)
plt.xlabel('Harmonic order')
plt.ylabel('Amplitude')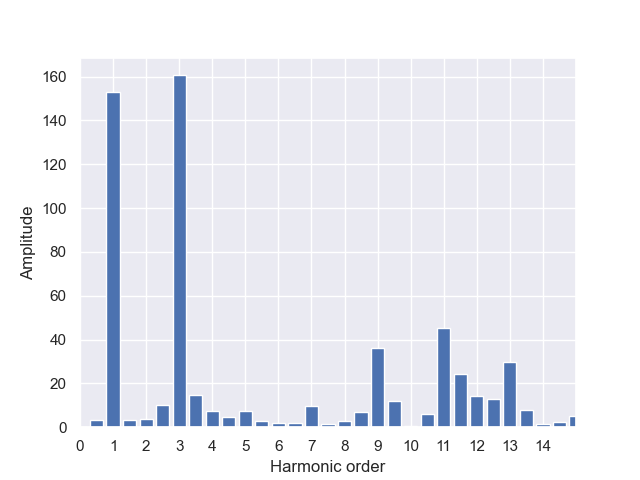

 分解出的结果就长上面的样子。

最后再多说几句，由于FFT的处理需要用到波形的所有数据，故进行处理时，如果原数据存在nan等异常数据时，FFT是出不了结果的，注意对原始数据的清洗。

最后

以上就是过时铃铛为你收集整理的Python_FFT的全部内容，希望文章能够帮你解决Python_FFT所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。