概述
- 概述
在数字信号处理领域中，FFT的运算常常会对输入信号序列进行补零操作，最常见的是补零后将FFT点数设置为N=2^k(k为正整数，2的整数次幂)。由于采集到的实验数据序列长度M往往不是2的整数次幂，因此可通过补零使FFT的长度变为2的整数次幂。
- 理论基础
首先来分析DFT与Z变换之间的关系。若x(n)为N点有限长序列，则其Z变换可由其N点DFT系数来表示：
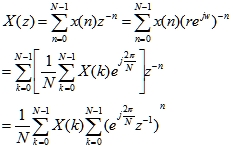
即
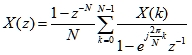
上式表明，N点序列的Z变换可由其N点DFT系数来表示。令z=ejw，则
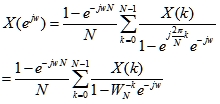
上式说明，连续谱X(ejw)也可以由其离散谱X(k)经插值后得到。
DFT是在Z平面单位圆上均匀分布的N个点，相隔为2π/N。假设对原数据序列x(n)补零，使序列长为2N，则序列有
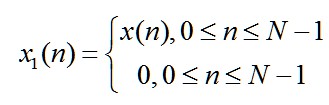
DFT运算结果为
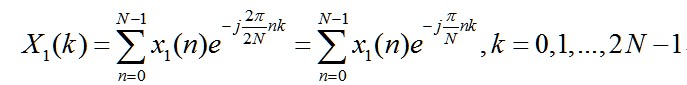
所以，补零就是对原有X(k)进行插值。
总结，L点DFT相当于单位圆中取了不相同的值，虽然在r不为整数时得到的频谱可能与原先的频谱看起来有所差别，但他们是有关联的，都是从X(ejw)取样得到的，只是取样的间隔不同而已。
- 仿真分析
3.1 FFT补零仿真
假设x(n)由两个余弦分量组成，他们的频率为f1=30Hz和f2=65.5Hz，采样频率为fs=200Hz，数据长度为N=200。用200和400进行FFT，比较它们的结果。
分析，数据长度N=200，当用L=400点进行FFT时，相当于在x(n)的200个数据样点后补了200个零值。Matlab代码如下
%
% pr2_2_12
clear all; clc; close all;
fs=200; % 采样频率
f1=30; f2=65.5; % 两信号频率
N=200; % 信号长度
n=1:N; % 样点索引
t=(n-1)/fs; % 时间刻度
x=cos(2*pi*f1*t)+cos(2*pi*f2*t); % 信号
X1=fft(x); % 按N点进行FFT
freq1=(0:N/2)*fs/N; % N点时正频率刻度
X1_abs=abs(X1(1:N/2+1))*2/N; % 信号幅值
L=2*N; % 补零后FFT长度
X2=fft(x,L); % 按L长进行FFT
freq2=(0:L/2)*fs/L; % L点时频率刻度
X2_abs=abs(X2(1:L/2+1))*2/N; % 信号幅值
% 作图
subplot 211; plot(freq1,X1_abs,'k');
grid; ylim([0 1.2]);
xlabel('频率/Hz'); ylabel('幅值');
title('(a) 补零前FFT谱图')
subplot 212; plot(freq2,X2_abs,'k');
grid; ylim([0 1.2]);
xlabel('频率/Hz'); ylabel('幅值');
title('(b) 补零后FFT谱图')
set(gcf,'color','w');
运行程序后得到信号序列x(n)在补零前、后的频谱图比较，如图1所示。图1上面小图中补零之前的频谱对f2信号是模糊的，由于频谱泄露，频带被拓宽了；图1下面小图中可以看到在65.5Hz处有一个峰值，这是因为补零以后能改善栅栏效应，使原先不清晰的谱线显现。
同时应该注意到频率刻度和计算幅值的变化。补零前，计算频率刻度freq=(0:N/2)*fs/N，计算出的信号幅值X1_abs=abs(X1(1:N/2+1))*2/N，其中N是信号长度，也是FFT点数。但补零至L=400后，FFT点数也是L=400，计算频率刻度freq2=(0:L/2)*fs/L，而计算出信号的幅值是X2_abs=abs(X2(1:L/2+1))*2/N，虽然数据长度在补零后增长到L，但其有效长度还应该是N，且计算幅值是要以有效长度来计算的。
此外，图1中f1只是一条谱线，而在图b中f1除了一个峰值外在它的周围还有一些波纹振荡，这是频谱泄漏造成的。
3.1 频谱泄漏仿真分析
频谱泄漏频谱分析过程中常见的现象之一，在对连续信号的采样序列进行DFT运算，由于信号长度必须为有限值，因此需要将连续信号序列截断，这样做的后果会使信号的频谱展宽，这种现象称作频谱泄漏。对信号做截断处理相当于将连续信号序列乘以一个窗函数，一般的窗函数类别有矩形窗、汉宁窗、汉明窗、布莱克曼窗等。由于窗函数是对称的，加窗后的有限长序列的傅里叶变换是实函数。理想情况下，连续信号的傅里叶变换在f1处有一个冲击函数，但当连续信号被截断并离散化后，信号的谱线已经不限于一个冲击函数，而是扩散了，这就是对连续信号截断（加窗）后出现的频谱泄漏现象。
在信号处理中，经常会遇到对信号加窗后，有的没有发生泄漏，但有的发生了泄漏。
举例：假设有一余弦信号，频率f0=30Hz，信号为x(t)=cos(2*pi*30t)，采样频率fs=128Hz，样本长度分别取N=128he N=100，在FFT后作谱图比较频谱差别，matlab程序如下。
%
% pr2_2_8
clear all; clc; close all;
fs=128; % 采样频率
% 第一部分
N=128; % 信号长度
t=(0:N-1)/fs; % 时间序列
y=cos(2*pi*30*t); % 信号序列
Y=fft(y,N); % FFT
freq=(0:N/2)*fs/N;
n2=1:N/2+1; % 计算正频率的索引号
Y_abs=abs(Y(n2))*2/N; % 给出正频率部分的频谱幅值
% 作图
subplot 211;
stem(freq,Y_abs,'k')
xlabel('频率(Hz)'); ylabel('幅值');
title('(a) Fs=128Hz, N=128')
axis([10 50 0 1.2]);
% 第二部分
N1=100; % 信号长度
t1=(0:N1-1)/fs; % 时间序列
y1=cos(2*pi*30*t1); % 信号序列
Y1=fft(y1,N1); % FFT
freq1=(0:N1/2)*fs/N1;
n2=1:N1/2+1; % 计算正频率的索引号
Y_abs1=abs(Y1(n2))*2/N1; % 给出正频率部分的频谱幅值
% 作图
subplot 212;
stem(freq1,Y_abs1,'k')
xlabel('频率(Hz)'); ylabel('幅值');
title('(b) Fs=128Hz, N=100')
axis([10 50 0 1.2]); hold on
line([30 30],[0 1],'color',[.6 .6 .6],'linestyle','--');
plot(30,1,'ko','linewidth',5)
set(gcf,'color','w');
运行上述程序后得到的频谱图为
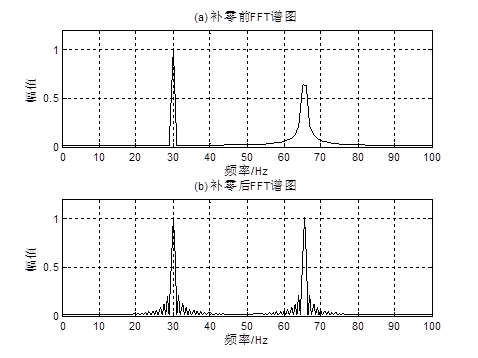
仿真结果分析，在程序中采用相同的信号，中心频率f0=30，采样频率fs=128Hz，差别仅在FFT的长度。在N=128的谱图上只在30Hz处有一条谱线，其它频点幅值都为0；而在N=100的谱图上有明显的泄露现象，谱线用黑实线表示，最大两根谱线在30Hz两侧，图中虚线和黑圈表示了30Hz的频率点。
为什么当N=128时FFT频谱无泄漏，而当N=100时FFT频谱会有泄漏?
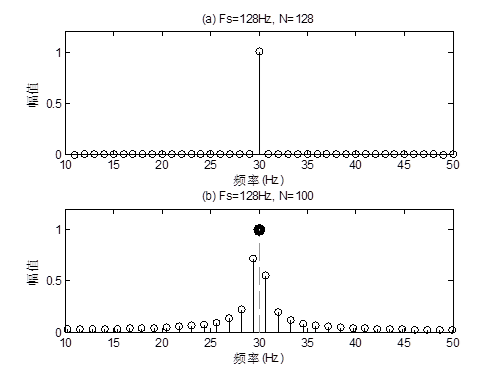
由信号处理理论知识可知，在经过加矩形窗之后，单点频信号的频谱如图3所示。此频谱图已不是一个单一的δ函数，而是由于泄漏的情况而导致展宽。
设信号的频率为f0，当取信号为整周期采样时，信号的频率f0=k*Δf，f0将于某一条谱线重合，如图3所示，第k条谱线频率为f0，是整周期采样后的频谱，虽然存在频谱泄漏的情况，但是由于信号的频率f0与第k条谱线重合，k+i（i为整数值）的任意谱线正好落在零点位置，所以在谱图中没有表现出泄漏现象，真实的泄漏是存在的。
当取信号为非整周期采样时，信号频率f0不与FFT后某条谱线重合，而是如图4所示那样，f0落在两条谱线中间位置，具体是落在第k和第k+1条谱线之间，其中第k条谱线是局部极大值。
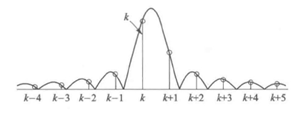
非整周期采样时，由于信号频率f0在两条谱线之间，第k条谱线虽然是局部极大值，但不与f0相重合，那么k+i（i为整数）的任意谱线都为频谱函数上的非零值，所以在频谱图中表现出了明显的泄漏现象，真实的泄漏也是存在的。
4、解决方法
FFT补零操作可能带来频谱的泄漏问题，为了防止泄漏，必须采取必要的补救方法，对于单点频信号来说可以调整采样频率使之构成整周期采样，但大多数实际处理中的信号不是单点频信号，而是多频率的，所以泄漏在所难免。当泄漏情况存在时，只能想法设法减小泄漏的影响，比如采取加窗的措施，矩形窗的泄漏最大，除此之外还可以使用汉宁窗、汉明窗、布莱克曼窗等窗函数。
最后
以上就是勤奋黄豆为你收集整理的FFT中的补零问题的全部内容，希望文章能够帮你解决FFT中的补零问题所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复