傅里叶变换终极必杀技

网上关于傅里叶变换的解释特别多，但大部分都比较偏理论，导致我看来N多教程也还是懵懵懂懂。在某本书（信号完整性分析？？？）中看到一句震耳发聩的话："每个工程师都应该亲自动手计算一遍傅里叶变换"。

我知道很多工具可以直接给出傅里叶变换结果，但不清不楚一直是我心里过不去的坎，今天终于把坎踏平了，已经忘记了这是第几次冲锋。。。20200324

本文主要对一个连续周期信号进行采样所得的有限离散周期信号进行离散傅里叶变换（DFT）变换，期间对用到的一些原理进行解释说明并有详细计算过程。基本包括了处理过程的所有细节。

这里说明一下：快速傅里叶变换FFT是一种利用矩阵知识快速实现离散傅里叶变换DFT的方法，最终结果是一样的，FFT只是一种实现DFT的算法。

首先假设我们已经了解了以下理论知识:

1. 采样定理（采样频率至少要大于原始信号最高频率的2倍才能提取出原始信号信息）；
2. 欧拉公式的应用:   

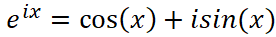
假设我们的原始信号是：

计算出上面两个正弦函数的周期分别是1 s和 2/3 s，所以函数 Xt 的周期是2 s（最小公倍数）。

根据采样定理，我们的采样频率就至少需要0.5 Hz才能保证这两个频率都被正确处理（采样频率越高，失真越小）。我们这里就定采样频率Fs为4 Hz吧（即每相邻两个采样点的采样时间间隔是0.25 s ，刚好两倍的采样频率结果观察起来不够明显）。

确定了采样频率，接下来就是采样点的个数了。对于周期信号，要使采样后的信号能完全还原出来，采样的范围必须至少包含一个周期吧。函数 Xt 的周期是2 s，采样频率4 Hz，于是得出采样点数N至少为8点。

下面开始计算啦！！！

傅里叶变换计算公式为：

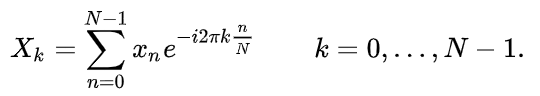
上式的就是我们采样点的值，就是傅里叶变换的结果。或许很多人看到这个式子这么复杂就头大，我也是[哭唧唧]。但我们的伟大领袖说过“一切数学公式都是纸老虎”。且看我将它大卸八块。（对于想要从感性上理解这个公式的同学，强烈建议上B站学习一下：https://www.bilibili.com/video/BV1pW411J7s8?from=search&seid=7806809382090131811）

我们这里就只讲计算了，毕竟理论的东西我自己还不能说很懂呢。。。

因为要用到，那我们就先要把  都计算出来：

                    第一个点：    = sin(2*pi*0) + sin(3*pi*0) + 1 = 1

                    第二个点：     = sin(2*pi*0.25) + sin(3*pi*0.25) + 1 =   2.7071

                    第三个点：    = sin(2*pi*0.5) + sin(3*pi*0.5) + 1 =   0

                    第四个点：    = sin(2*pi*0.75) + sin(3*pi*0.75) + 1 =   0.70711

                    第五个点：    = sin(2*pi*1) + sin(3*pi*1) + 1 =   1

                    第六个点：    = sin(2*pi*1.25) + sin(3*pi*1.25) + 1 =   1.2929

                    第七个点：    = sin(2*pi*1.5) + sin(3*pi*1.5) + 1 =   2

                    第八个点：    = sin(2*pi*1.75) + sin(3*pi*1.75) + 1 =   -0.70711

好了现在可以开始计算傅里叶变换了：（N = 8）

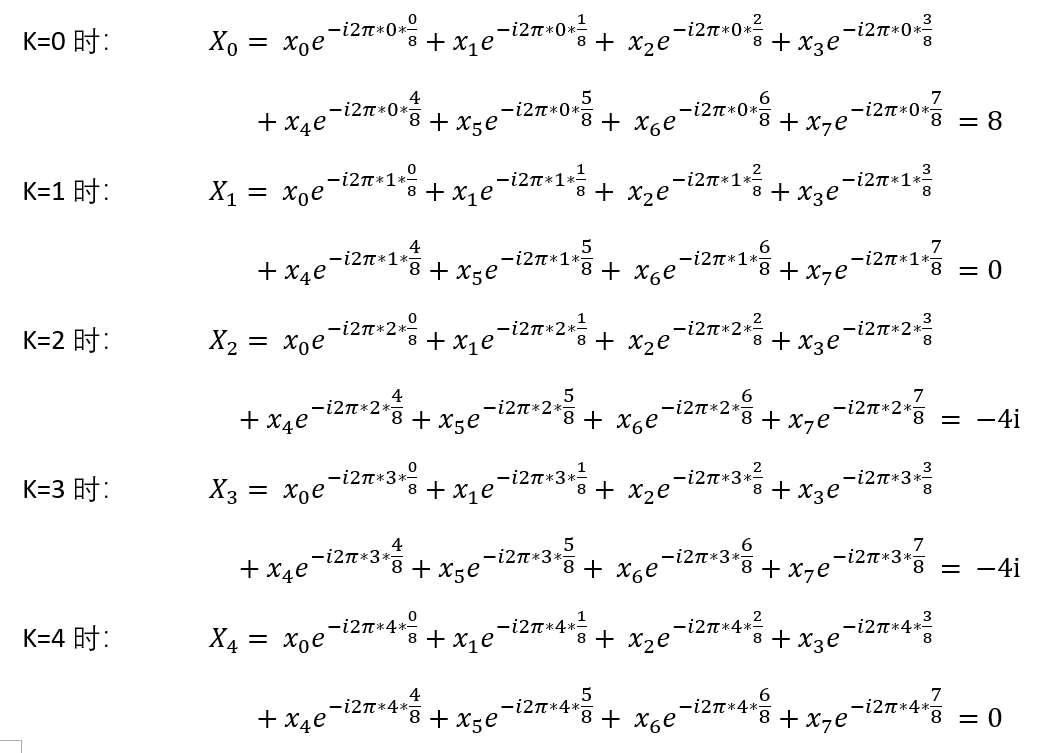
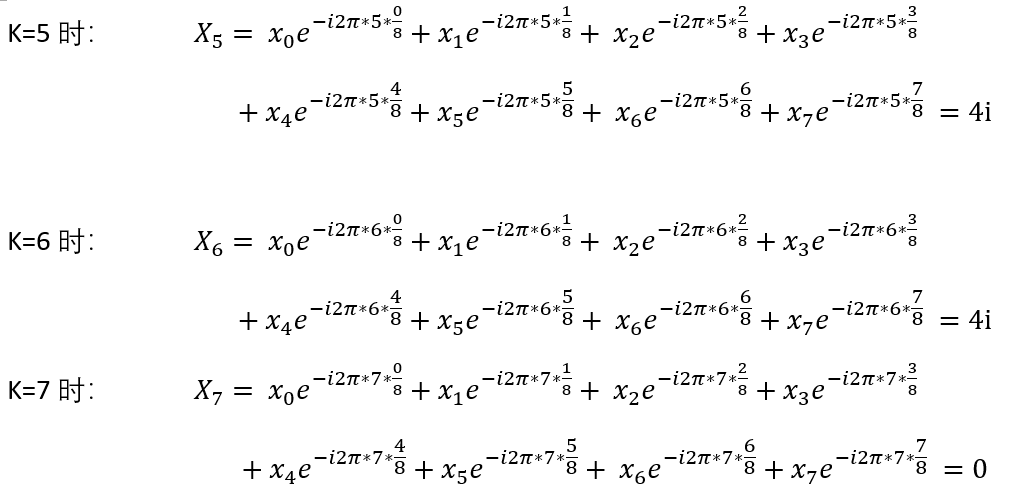
（虽然看起来上面的计算狠复杂（其实真的很复杂呀），但至少上面没有未知数，结果是一定存在的，不管是按计算器，matlab工具，或者欧拉公式，只有能计算出正确结果，就是好方法。）

坚持住，到了这里基本就要结束啦！

接下来对结果稍加整理，就是我们需要的频谱图啦！

由：           可得：

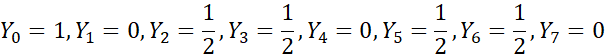
根据上面推荐的B站视频可知，傅里叶变换是计算的N个点的向量和，所以之前计算得到的结果要除以采样点数N，abs是求模长（绝对值）的函数，因为频谱图纵坐标的幅值是正值。（好吧我知道解释的很牵强，其实我也不知道为啥要这样。。。这个教程只负责指导你亲手计算一次傅里叶变换，关于理论知识，其他教程说的比我精彩）

上面就是频谱图的一些点了，但是我怎么知道每一个点对应什么频率呢?

其实傅里叶变换后的频率分辨率是（其中为采样的总时长）。为啥呢？

对以上的结果可以理解为：我们采样的数据只有 秒，信号的成分中周期最大也就是秒，频率最低就是。那么频率分辨率就是 了。也就是说频率分辨率只和总采样时间有关。采样时间越长，能区分的频率就越小，即分辨率越好。

这里假设采样周期为T，采样总时长为，那么就有如下关系：

本例子中解释分辨率就是：傅里叶变换的第一个结果表示频率为0的信号幅值，第二个结果就是表示频率为Fs/N = 4/8 = 0.5Hz 的信号幅值了，依次第三个结果表示1Hz信号幅值。。。第八个表示频率为3.5Hz信号的幅值。

我们把上面的结果在坐标轴中画出来，就是我们说的频谱图啦：（Fs = 4Hz, N = 8, 对称处理前）

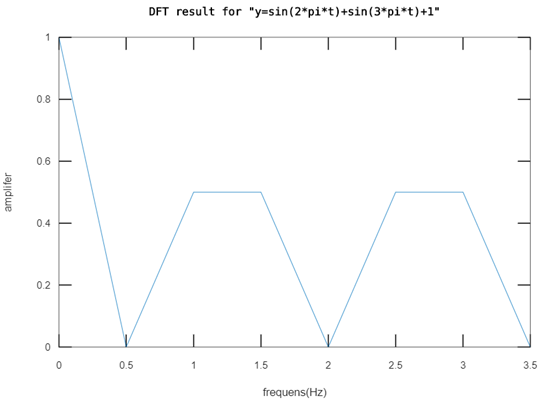
我们发现f=0.5到f=3.5的结果关于f=2对称，即X(N-k) = X(k)   (其中k=1:N-1)。

（对称的理论证明，传送门在此：https://www.zhihu.com/question/264560305 ）

我们看频率为0的时候幅值为1，表示原始信号中有一个幅值为1的直流信号，和我们的给出的原始信号相符（加了一个常数1）。

频谱图中频率为1时幅值是0.5，但我们的原始信号频率为1（ sin(2*pi*t) ）的分量幅值可是1啊。这是为啥呢？这是由上面说的对称所引起的。频谱图中频率为1和频率为3的点对称，两个点幅值都是0.5，两个加起来，就刚好是原始信号的幅值1了。同理sin(3*pi*t)的幅值是由频谱图中频率为1.5Hz和频率为2.5Hz的两个幅值相加而来，幅值也是1。

但图形既然对称，为啥我们要选择相信原始信号是由频率为1Hz和频率为1.5Hz的正弦波合成的，而不是频率为2.5Hz和3Hz呢？我们的采样频率是4Hz，根据采样定理，最大只能处理到2Hz的情况，所以我们只能选择1Hz和1.5Hz啦。

上面已经是频谱图了，但是不够完美，既然我们只需要对称的前半部分，那就再处理一下吧：

我们只取上面结果的频率在2Hz前的部分，且对频率不为0的信号幅值加倍，就得到了最终结果：（Fs = 4Hz, N = 8）

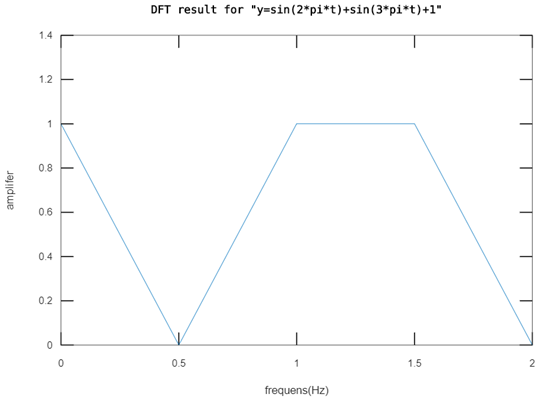
怎么样，这个结果够完美了吧！！！

但是这个实验的采样点太少导致频率分辨率太低（频率为0.75的幅值是什么呢，我们不知道，图中只是把前后两个点连线过渡而已，并不表示中间区域的幅值。注意：周期信号在频域中一定是离散的）。

频率分辨率太低怎么办呢？ 根据之前的分析知道，需要加长总的采样时间，那就保持采样频率不变，采样点数加到16试试吧，结果如下：（Fs = 4Hz, N = 16）

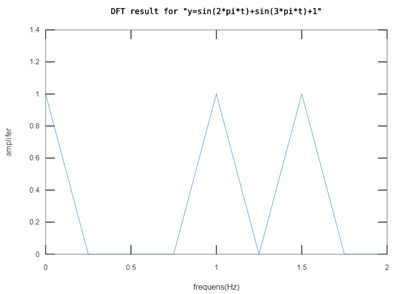
现在，从图中我们已经可以看出频率为0.75的信号分量幅值为0，基本能够确定原始信号中只有这三个波峰对应的频率分量了。

再把采样点加到512个点，结果如下：（Fs = 4Hz, N = 512）

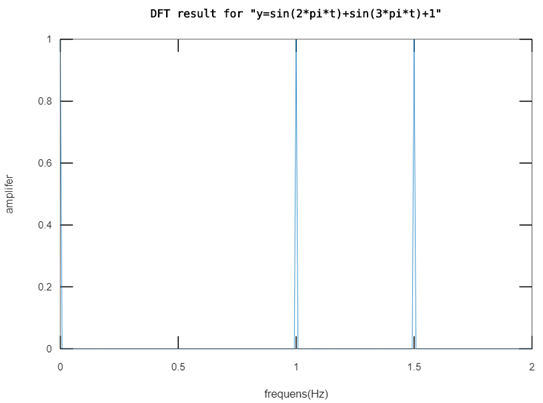
这下够清楚了吧。。。

在此附上matlab代码：（ %后跟注释，如有需要可以删除%查看中间结果，但中文前面的那个%不能删除）

-------------------------程序开始（可在线运行https://octave-online.net/ ）------------------------------

Fs = 4;                                % 设置采样率

T = 1/Fs;                            % 采样周期

N = 512;                            % 设置采样点数，设为8即可得到上面的实验结果

t = (0:N-1)*T;                   % 确定采样值，: 表示变量的取值范围

%t                                       % matlab中变量不加分号时会打印出变量的值

y = sin(2*pi*t)+sin(3*pi*t)+1;     % 本例子的原始信号，可以看出f = 0Hz, f=1Hz, f=1.5Hz 的信号分量

%y

Y = fft(y);                           % FFT是通过矩阵计算傅里叶变换的一种算法，和DFT结果是一样的

%Y                                      % 把Y前面的百分号去掉，就可以快速得到上面的计算结果啦！

Y1 = Y/N;                           % 上面有说，我也不知道为啥要除以N

%Y1

P2 = abs(Y1);                    % 求复数的模长

%P2

%f = Fs*(0:N-1)/N;          % 频率分辨率为Fs/N,  频率范围是0到Fs(N-1)/N

%plot(f,P2);                      % 以f为x轴坐标的格点，画出对称的变换结果

%xlabel('frequens(Hz)');              % 设置x轴坐标名称

%ylabel('amplifer');                      % 设置y轴坐标名称

%title('DFT result for "y=sin(2*pi*t)+sin(3*pi*t)+1"');                 % 设置图像标题

P1 = P2(1:N/2+1);                          % 把对称的部分图形去掉

%P1

P1(2:end-1) = 2*P1(2:end-1);      % 从第二个结果开始幅值都加倍（end表示最后一个值）

%P1

f = Fs*(0:N/2)/N;                           % 频率分辨率为Fs/N,  频率范围是0到Fs/2

%f

plot(f,P1);                                       %以f为x轴坐标的格点，画出去掉对称部分的变换结果

xlabel('frequens(Hz)');

ylabel('amplifer');

title('DFT result for "y=sin(2*pi*t)+sin(3*pi*t)+1"');

-------------------------------------------------程序完------------------------------------------------------------

恭喜我们都学习完啦，写这篇总结的时候对傅里叶变换也有了更深刻的认识，好开心呀！

本文参考的资料如下：

https://ww2.mathworks.cn/help/matlab/ref/fft.html

最后

以上就是大胆过客为你收集整理的傅里叶变换终极必杀技的全部内容，希望文章能够帮你解决傅里叶变换终极必杀技所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。