频谱泄露、栅栏效应、补零实验

理想情况

假设一个信号由两个频率不一样的余弦波组成$cos(2\pi ft)=cos(2\pi f_{1}t)+cos(2\pi f_{2}t)$组成，其中$f_1=50Hz,f_2=65Hz$我们以采样率$f_s=500Hz$对该信号进行采集，采样时间长度$T=0.4s$，对该信号做FFT后得到的信号如下图所示，此时在频谱上可以清楚地找到两个信号频率对应的位置。

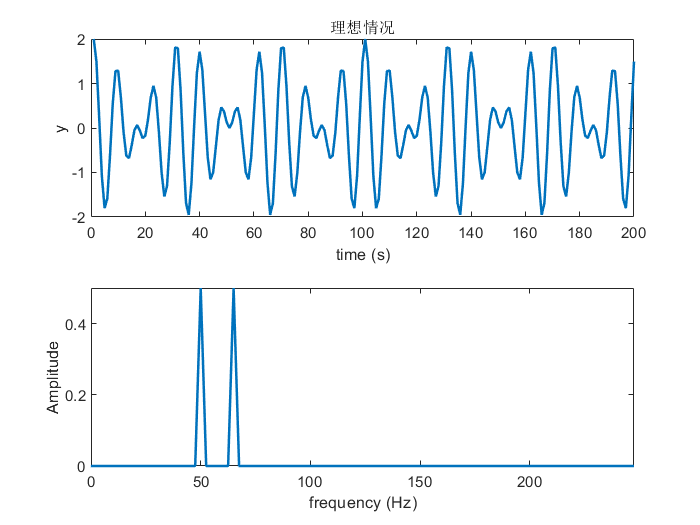
代码：

%% 理想情况
% 当采样时间正好为周期的整数倍时，没有频谱泄露；
% 因为序列时实值信号，所以FFT结果关于N/2对称，fftshift之后关于0对称
f0 = 50; f1 = 65; fs = 500; T = 0.4;
S = @(t) cos(2*pi*f0.*t) + cos(2*pi*f1.*t);
t = 0:1/fs:T-1/fs;
y = S(t);

nsamps = numel(y);
y_spec = fft(y);
y_spec = fftshift(y_spec)./nsamps;
f = ((0:nsamps-1)-nsamps/2)/T; 

figure(1);
subplot(2,1,1);plot(y,'linewidth',1.5); xlabel('time (s)'); ylabel('y');title('理想情况');
subplot(2,1,2);plot(f, abs(y_spec),'linewidth',1.5); xlabel('frequency (Hz)'); ylabel('Amplitude');
axis([0,inf,0,inf]);

频谱泄露

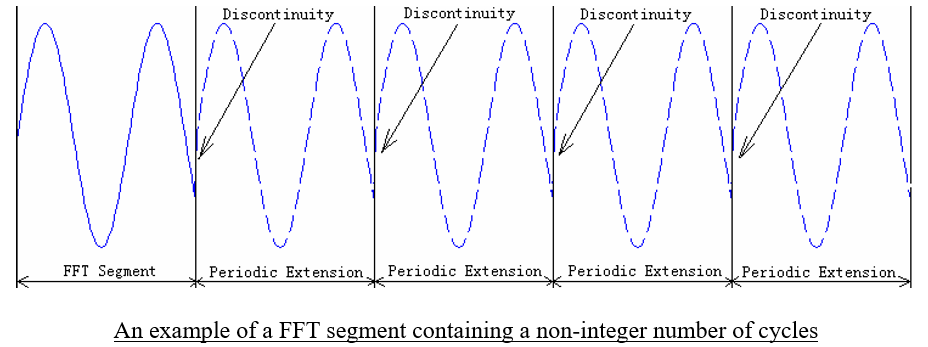
频谱泄露是对无限长信号进行截取操作时引入的旁瓣干扰，其在频域上的表现为除了主要频率之外还有不希望存在的频率成分。当对非周期信号进行截取操作时，无论怎么截取都会引起频谱泄露。当对周期信号进行截取操作时，如果截取时间长度为原信号周期的整数倍，则不会产生频谱泄露，反之则会。（因为DFT默认对截断的时域信号进行了周期延拓，在整数倍周期处截断再进行延拓可以完整地恢复出原始信号，反之如果在非周期处截断信号并延拓得到就不是原先的信号了）。

这里依然以上述信号为例。假设此时采样时间变成了0.3s，那么在该时间窗口内，$cos(2\pi f_{1}t)$可以被截断为整数倍信号周期，然而$cos(2\pi f_{2}t)$则不是整数倍的信号周期。此时对采样信号做FFT结果如下。可以看到频谱上$f=50Hz$处幅度大于$f=65Hz$的幅度，$cos(2\pi f_{2}t)$的能量被泄露到了其他频点上。

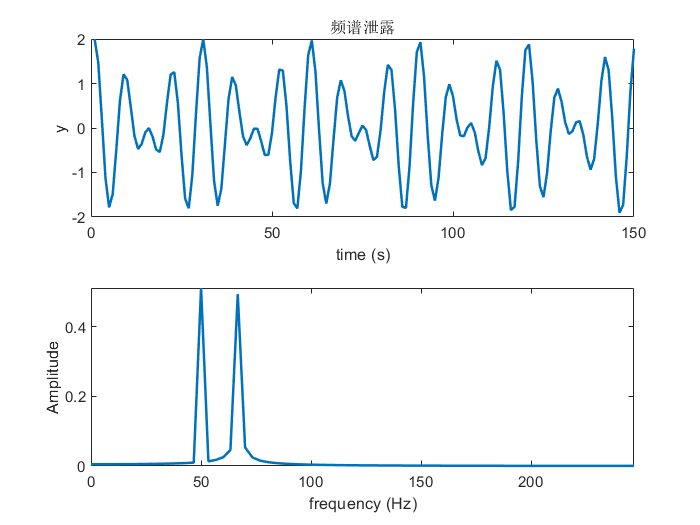
代码：

%% 频谱泄露
% 当采样时间不是周期的整数倍时，发生了频谱泄露；
f0 = 50; f1 = 67; fs = 500; T = 0.3;
S = @(t) cos(2*pi*f0.*t) + cos(2*pi*f1.*t);
t = 0:1/fs:T-1/fs;
y = S(t);

nsamps = numel(y);
y_spec = fft(y);
y_spec = fftshift(y_spec)./nsamps;
f = ((0:nsamps-1)-nsamps/2)/T; 

figure(2);
subplot(2,1,1);plot(y,'linewidth',1.5); xlabel('time (s)'); ylabel('y');title('频谱泄露');
subplot(2,1,2);plot(f, abs(y_spec),'linewidth',1.5); xlabel('frequency (Hz)'); ylabel('Amplitude');
axis([0,inf,0,inf]);

频谱泄露的解决方法1：改变采样时长

既然频谱泄露是由于采样时长不是信号整数倍周期导致的，那么只要将采样时长变成各主频信号周期的最大公倍数就可以了。比如我们将采样时长缩短为0.2s，此时做FFT得到下图，虽然采样时长变短导致频率分辨率降低，但是频谱泄露的问题解决了。

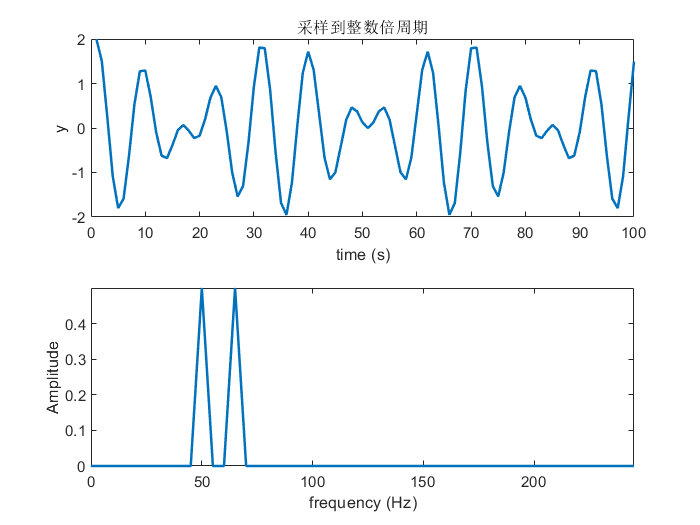
代码：

%% 抑制频谱泄露——方案一：采样到两个信号成分的整数倍周期
% 改变采样时长，使采样时长为各主频信号周期的整数倍
f0 = 50; f1 = 65; fs = 500; T = 0.2;
S = @(t) cos(2*pi*f0.*t) + cos(2*pi*f1.*t);
t = 0:1/fs:T-1/fs;
y = S(t);

nsamps = numel(y);
y_spec = fft(y);
y_spec = fftshift(y_spec)./nsamps;
f = ((0:nsamps-1)-nsamps/2)/T; 

figure(3);
subplot(2,1,1);plot(y,'linewidth',1.5); xlabel('time (s)'); ylabel('y');title('采样到整数倍周期');
subplot(2,1,2);plot(f, abs(y_spec),'linewidth',1.5); xlabel('frequency (Hz)'); ylabel('Amplitude');
axis([0,inf,0,inf]);

频谱泄露的解决方法2：加窗

对时域信号采样实际上默认对原信号增加了矩形窗，但是矩形窗的旁瓣能量较高，因此在采样时长不是信号整数倍周期时频谱泄露的效应比较明显。为了降低频谱泄露对主频率的影响，可以通过加入各种窗口的方法抑制旁瓣能量，常用的窗口包括汉宁窗、哈明窗、布莱克曼窗等，这里以哈明窗为例展示加窗作用。可以看到相比原先存在频谱泄露的频谱，加窗以后频谱能量更加集中了。（比如看75Hz处的幅度，加窗之后明显比没加窗时幅度低）

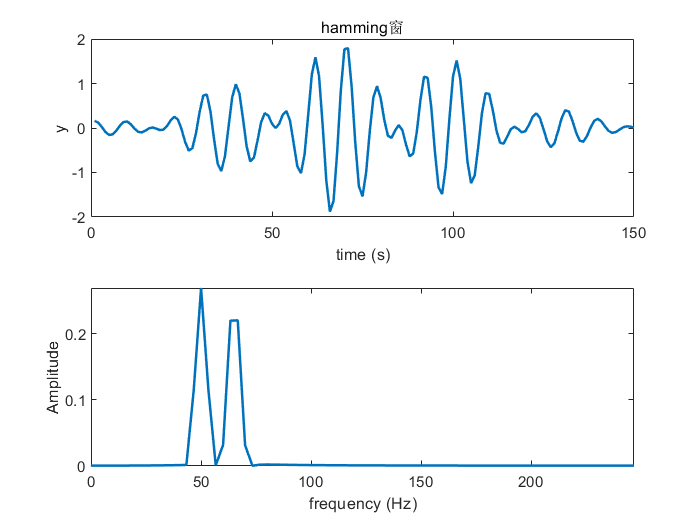
代码：

%% 抑制频谱泄露——方案二：加窗抑制频谱泄露
f0 = 50; f1 = 65; fs = 500; T = 0.3;
S = @(t) cos(2*pi*f0.*t) + cos(2*pi*f1.*t);
t = 0:1/fs:T-1/fs;
y = S(t);

w = hamming(fs * T);
y_hamm = y.*w.';

nsamps = numel(y_hamm);
y_spec = fft(y_hamm);
y_spec = fftshift(y_spec)./nsamps;
f = ((0:nsamps-1)-nsamps/2)/T; 

figure(4);
subplot(2,1,1);plot(y_hamm,'linewidth',1.5); xlabel('time (s)'); ylabel('y');title('hamming窗');
subplot(2,1,2);plot(f, abs(y_spec),'linewidth',1.5); xlabel('frequency (Hz)'); ylabel('Amplitude');
axis([0,inf,0,inf]);

更加直观地理解加窗的作用，可以认为加窗后，强行将阶段信号两端的信号幅度收敛到了0附近，增加了延拓后信号在衔接处的连贯性。 比如原先没加窗的信号是这样的：


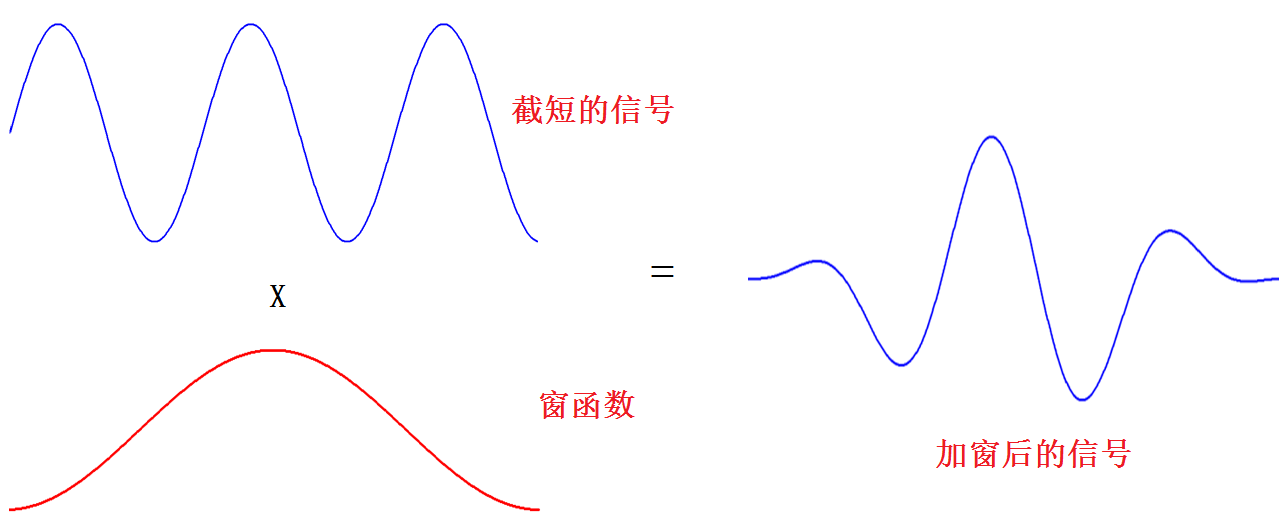
加入窗函数之后变成：

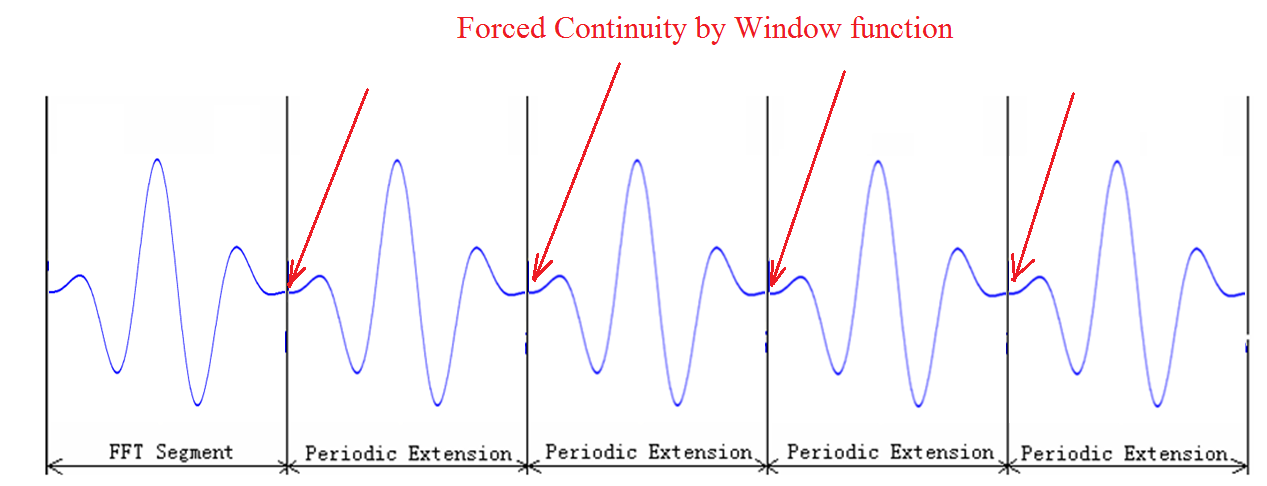
强行使得信号连接上，从而降低了阶段处非整数倍信号周期的影响。

栅栏效应——补零

我们注意到加窗后得到的频谱依然无法得到$65Hz$的频率分量。这是因为信号的采样时长为0.3s，因此物理分辨率是$f_s/N=1/T=3.333Hz$。此时65Hz不是整数倍的分辨率，因此无法在频谱上体现出来。这就是栅栏效应，解决该问题的常用方法为时域补零。（注意：时域补零不会增加信号的物理分辨率，但是会增加信号的计算分辨率，信号的物理分辨率只和采样时长有关）我个人觉得这里可以理解为DFT是对DTFT频域上的采样，补零相当于增加了采样点，如果DTFT本身就无法将两个频率成分区别开的话，那么频域上插再多的值（时域上补再多的零）也没有用。这里我们知道两个信号之间的频差为15Hz，大于3.33Hz所以理论上可以在频谱上将两个频点区分开，但是由于采样点数的限制，65Hz落在了两个采样的频点之间，为了将65Hz的频率成分提取出来，这里可以进行补零操作。结果如下：

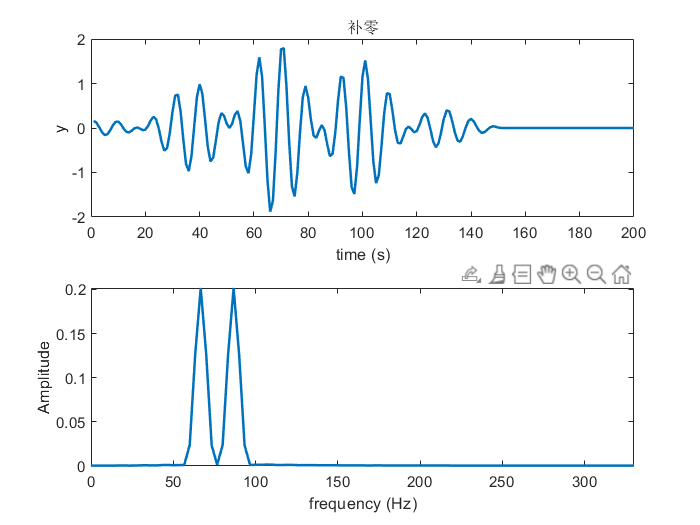
代码：

%% 出现了栅栏效应——补零
f0 = 50; f1 = 65; fs = 500; T = 0.3;
S = @(t) cos(2*pi*f0.*t) + cos(2*pi*f1.*t);
t = 0:1/fs:T-1/fs;
y = S(t);

w = hamming(fs * T);
y_hamm = y.*w.';
y_hamm_add_0 = [y_hamm, zeros(1,fs*T/3)];

nsamps = numel(y_hamm_add_0);
y_spec = fft(y_hamm_add_0);
y_spec = fftshift(y_spec)./nsamps;
f = ((0:nsamps-1)-nsamps/2)/T; 

figure(5);
subplot(2,1,1);plot(y_hamm_add_0,'linewidth',1.5); xlabel('time (s)'); ylabel('y');title('补零');
subplot(2,1,2);plot(f, abs(y_spec),'linewidth',1.5); xlabel('frequency (Hz)'); ylabel('Amplitude');
axis([0,inf,0,inf]);

通过在时域信号上补零，65Hz的频率成分被分辨出来了。但是这里依然存在频谱泄露。说明补零只能缓解栅栏效应，但是不能解决频谱泄露的问题。

栅栏效应和频谱泄露的关系

（这是我的猜测，如果有不对的地方，还望大佬纠正。）如果不考虑补0操作，那么栅栏效应一定会导致频谱泄露，反之也成立 证明：

设信号对应的角频率为${\omega }_0$，采样点数为$N$。那么当信号频率不是频率分辨率的整数倍时，会产生栅栏效应，此时可得
$${\omega }_0\ne k\frac{2\pi }{N}$$
由${\omega }_0=2\pi f_0/f_s$可得
$$2\pi f_0/f_s\ne k\frac{2\pi }{N}$$
$f_s$为采样频率，$f_0$为原信号频率

$$f_0\ne k\frac{f_s}{N}$$

$T$为采样时长，$T_0$为原始信号周期
$$\frac{1}{T_0}\ne k\frac{1}{T}$$
$$T\ne k{T}_0$$

所以可得采样时长不是信号周期的整数倍，所以同样会产生频谱泄露，反之也成立。其中栅栏效应可通过补零的操作缓解，而频谱泄露可通过改变采样时长或者加窗缓解。

总结

解决频谱泄露和栅栏效应最有效的方法是改变采样时长，使得采样时长为整数倍信号周期，但是这在实际过程中常常难以实现，所以需要用加窗和补零的操作分别缓解频谱泄露和栅栏效应。

最后

以上就是甜蜜棒球为你收集整理的频谱泄露、栅栏效应、补零实验的全部内容，希望文章能够帮你解决频谱泄露、栅栏效应、补零实验所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。