1.傅立叶变换FT(Fourier Transform)
性质:时域连续,频域连续
周期信号只有傅立叶级数,严格意义上讲,没有傅立叶变换;但可以令周期信号的周期趋于无穷大,这样,将周期信号变为非周期信号,再通过引入奇异函数(如单位冲激函数、阶跃函数等带有突变特性的函数),求其傅立叶变换。
例:正余弦函数的傅立叶变换
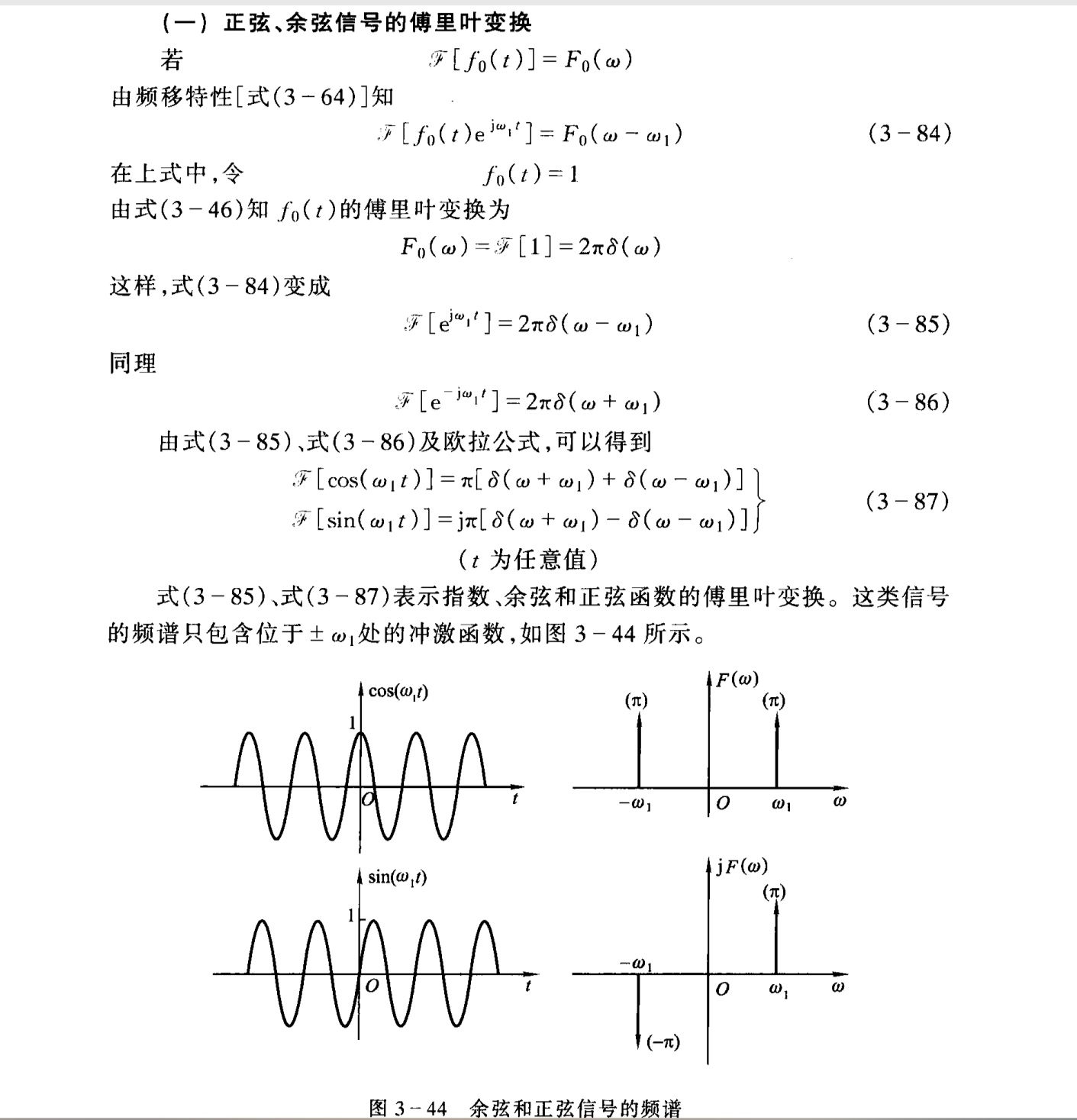
时域和频域在很多性质上都具有对偶的关系,如:时域卷积对应频域乘积、时域乘积对应频域卷积的1/2pi.
2.离散时间傅立叶变换DTFT
时域离散,频域连续
相当于对时域的连续信号进行抽样(等间隔采样)后,再进行傅立叶变换。
3.离散傅立叶变换DFT
时域离散,频域也离散
DFT完全是应数字信号处理的发展而来的(要求幅值和时间都是离散的),因为如果没有计算机,用DTFT分析看频率响应就可以,为了适应计算机计算,那么就必须要用离散的值,因为计算机不能处理连续的值。
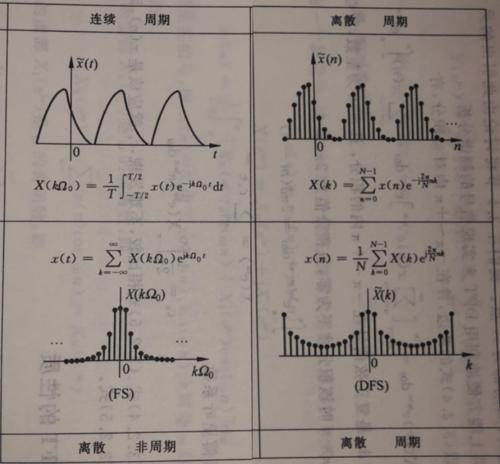 图左侧为信号的连续傅立叶变换(FT),右侧为DFT效果。
图左侧为信号的连续傅立叶变换(FT),右侧为DFT效果。
IDFT即离散傅里叶逆变换。
4.快速傅立叶变换FFT
DFT的一种快速算法。
在MATLAB中经常用FFT()函数进行频谱分析。
用FFT实现音乐频谱的显示。
此外还有FS傅里叶级数和DFS离散傅立叶级数,两者不是一个概念,FS是表示任意周期信号都可展开为傅里叶级数,而DFS是指离散周期序列可通过离散傅立叶级数获得其频谱:
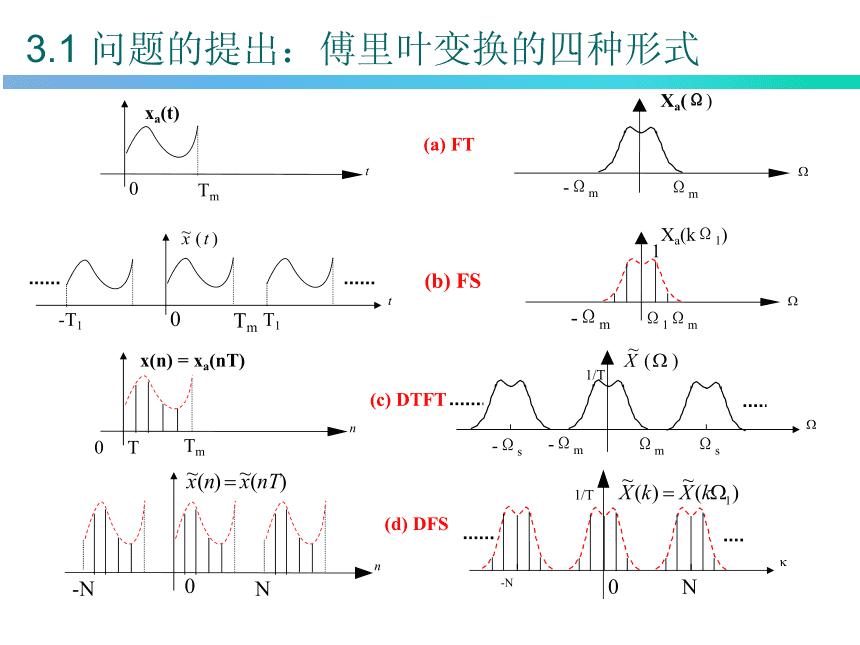
最后
以上就是壮观音响最近收集整理的关于FT,DTFT,DFT,IDFT,FFT含义的全部内容,更多相关FT内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复