题目描述
XOR(异或)是一种二元逻辑运算,其运算结果当且仅当两个输入的布尔值不相等时才为真,否则为假。 XOR 运算的真值表如下(
1
1
表示真, 表示假):
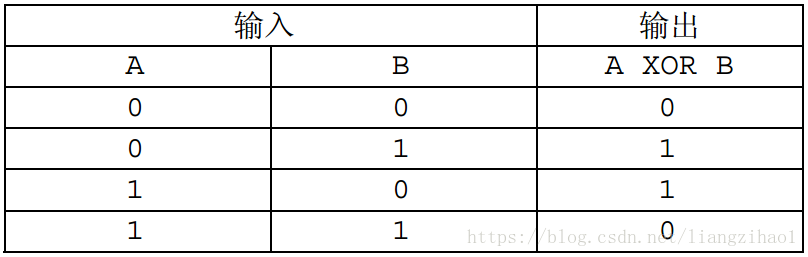
而两个非负整数的 XOR 是指将它们表示成二进制数,再在对应的二进制位进行 XOR 运算。
譬如
12
12
XOR
9
9
的计算过程如下:
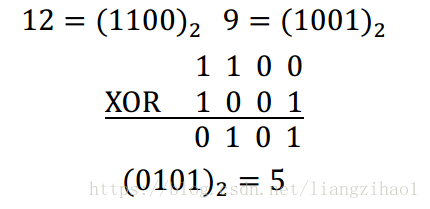
故 XOR
9=5
9
=
5
。
容易验证, XOR 运算满足交换律与结合律,故计算若干个数的 XOR 时,不同的计算顺序不会对运算结果造成影响。从而,可以定义
K
K
个非负整数 的 XOR 和为
A1
A
1
XOR
A2
A
2
XOR …… XOR
AK−1
A
K
−
1
XOR
AK
A
K
。
考虑一个边权为非负整数的无向连通图,节点编号为
1
1
到 ,试求出一条从
1
1
号节点到 号节点的路径,使得路径上经过的边的权值的 XOR 和最大。
路径可以重复经过某些点或边,当一条边在路径中出现了多次时,其权值在计算 XOR 和时也要被计算相应多的次数,具体见样例。
输入输出格式
输入格式:
输入文件 xor.in 的第一行包含两个整数
N
N
和 , 表示该无向图中点的数目与边的数目。
接下来
M
M
行描述 条边,每行三个整数
Si,Ti,Di
S
i
,
T
i
,
D
i
,表示
Si
S
i
与
Ti
T
i
之间存在一条权值为
Di
D
i
的无向边。
图中可能有重边或自环。
输出格式:
输出文件 xor.out 仅包含一个整数,表示最大的 XOR 和(十进制结果)。
输入输出样例
输入样例#1:
5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2
输出样例#1:
6
说明
【样例说明】
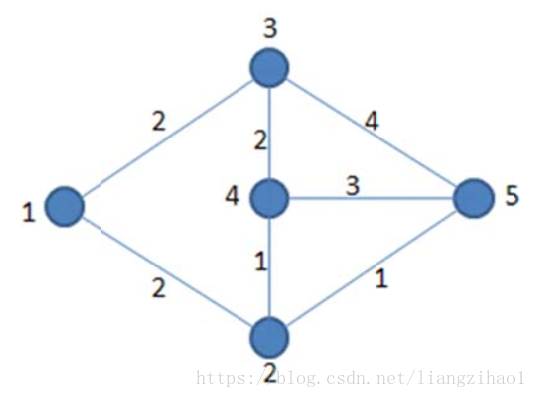
如图,路径
1→2→4→3→5→2→4→5
1
→
2
→
4
→
3
→
5
→
2
→
4
→
5
对应的XOR和为
2 2 XOR XOR 2 2 XOR XOR 1 1 XOR XOR 3=6 3 = 6
当然,一条边数更少的路径 1→3→5 1 → 3 → 5 对应的XOR和也是 2 2 XOR 。
【数据规模】
对于 20% 20 % 的数据, N≤100,M≤1000,Di≤104 N ≤ 100 , M ≤ 1000 , D i ≤ 10 4 ;
对于 50% 50 % 的数据, N≤1000,M≤10000,Di≤1018 N ≤ 1000 , M ≤ 10000 , D i ≤ 10 18 ;
对于 70% 70 % 的数据, N≤5000,M≤50000,Di≤1018 N ≤ 5000 , M ≤ 50000 , D i ≤ 10 18 ;
对于 100% 100 % 的数据, N≤50000,M≤100000,Di≤1018 N ≤ 50000 , M ≤ 100000 , D i ≤ 10 18 。
分析:
一堆数的异或和就可以考虑线性基了,因为线性基只有
log2Di
l
o
g
2
D
i
,也就是最多
64
64
个。我们发现,任意路径都可以表示为一条从
1
1
到的简单路径加若干个环。
如果
1
1
到的简单路径与某个环有边相交,相当于另一条简单路径。
如果一个环不在路径上,我们可以先走到这个环上,转一圈后原路返回,走两次的边就被抵消了。
如果两个环有交,那么相当于一个新的环。
所以我们枚举环,加入到线性基里,然后取异或最大值,从高位开始算,因为某一位能拿到
1
1
比这位拿到一定更优。
至于枚举环,我们可以建一棵dfs搜索树,对于任何一条非树边,与树上路径连成一个环,这些环可以代替所有环。因为假设我们有一个一条非树边
(x,y)
(
x
,
y
)
加上
x
x
到树上路径的环和一个一条非树边
(y,z)
(
y
,
z
)
加上
y
y
到树上路径的环,异或起来就是一个
(x,z)
(
x
,
z
)
树上路径+若干
(x,z)
(
x
,
z
)
非树边连成路径的环。
代码:
#include <iostream>
#include <cmath>
#include <cstdio>
#define LL long long
const int maxn=5e4+7;
const int maxe=1e5+7;
const int maxp=62;
using namespace std;
int n,m,x,y;
int ls[maxn],vis[maxn];
LL dis[maxn],a[maxn],bit[maxn];
LL ans,w;
struct edge{
int y,next;
LL w;
}g[maxe*2];
void push(LL x)
{
if (x==0) return;
int c=0;
for (int i=1;i<=maxp;i++)
{
if (x&bit[maxp-i])
{
if ((!a[i]) && (!c)) c=i;
x^=a[i];
}
}
a[c]=x;
for (int i=1;i<=maxp;i++)
{
if (i==c) continue;
if (a[i]&bit[maxp-c]) a[i]^=a[c];
}
}
void dfs(int x,LL rec)
{
dis[x]=rec;
vis[x]=1;
for (int i=ls[x];i>0;i=g[i].next)
{
int y=g[i].y;
if (!vis[y]) dfs(y,rec^g[i].w);
else push(rec^g[i].w^dis[y]);
}
}
int main()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=m;i++)
{
scanf("%d%d%lld",&x,&y,&w);
g[i].y=y;
g[i].w=w;
g[i].next=ls[x];
ls[x]=i;
g[i+m].y=x;
g[i+m].w=w;
g[i+m].next=ls[y];
ls[y]=i+m;
}
bit[0]=1;
for (int i=1;i<=maxp;i++) bit[i]=bit[i-1]*2;
dfs(1,0);
ans=dis[n];
for (int i=1;i<=maxp;i++) ans=max(ans,ans^a[i]);
printf("%lld",ans);
}最后
以上就是无私紫菜最近收集整理的关于洛谷 P4151 [WC2011]最大XOR和路径 线性基的全部内容,更多相关洛谷内容请搜索靠谱客的其他文章。




![洛谷 P4151 [WC2011]最大XOR和路径 线性基](https://www.shuijiaxian.com/files_image/reation/bcimg8.png)

![[线性基] Luogu P4151 最大XOR和路径题解代码](https://www.shuijiaxian.com/files_image/reation/bcimg10.png)
![【线性基】【洛谷P4151】[WC2011]最大XOR和路径](https://www.shuijiaxian.com/files_image/reation/bcimg11.png)
发表评论 取消回复