Tensorflow实现K近邻分类器

1. K近邻分类模型基本原理

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

2. K近邻分类模型的三个基本要素

（a） 距离度量 (b) K值的选择 （c）分类决策规则

2.1 距离度量

假定特征空间$X$是M维实向量空间：$X$ $ϵ$$R^M$，任意两个样本（$i,j$）的特征向量记为：$x_i=(x_{i,1},...x_{i,M})$${}^T$和$x_i=(x_{i,1},...x_{i,M})$${}^T$，$x_i$和$x_j$之间的距离定义为:
$$L_p(x_i,x_j)=(\sum _{m=1}^M{\left|x_{i,m}-x_{j,m}\right|}^p{)}^{\frac{1}{p}}$$
$P=2$时为欧式距离：
$$L_2(x_i,x_j)=(\sum _{m=1}^M{\left|x_{i,m}-x_{j,m}\right|}^2{)}^{\frac{1}{2}}$$
$P=1$时为欧式距离：
$$L_1(x_i,x_j)=(\sum _{m=1}^M\left|x_{i,m}-x_{j,m}\right|)$$
$P=$$\infty$时为欧式距离：
$$L_{\infty }(x_i,x_j)=max\left|x_{i,m}-x_{j,m}\right|$$

在这里选择$L1$距离

2.2 K值的选择

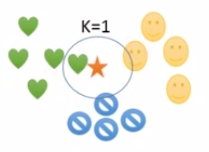
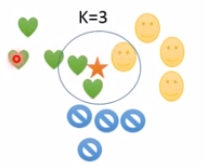
上图中测试样本为五角星，其余均为训练样本，上面三张图分别是K=1,K=3时测试样本所属的类别，当K=1时根据最近邻分类原则把测试样本化分为心状类别,K=3时也属于心状。所以对于K值的选择，会影响到最终的分类。一般而言K值选择的越小，整体模型越复杂，容易发生过拟合，K值越大，模型越简单，i尼斯误差会增大，但容易发生误分类。

2.3 分类决策规则

1. 多数表决规则：
   
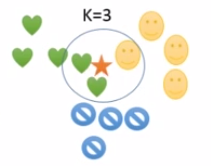
   五角星属于心状

2. 距离加权规则：
   
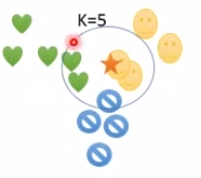
   五角星属于圆脸

3. 计算步骤

1. 算距离：给定测试样本特征向量,计算它与训练集中每个样本特征向量的距离
2. 找邻居：圈定距离最近的K个训练样本，作为测试样本的近邻
3. 做分类：根据这K个近邻归属的主要类别，来对测试样本分类

4. TensorFlow实现

	import tensorflow as tf
	import os
	import numpy as np
	os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
	
	from tensorflow.examples.tutorials.mnist import input_data
	mnist=input_data.read_data_sets('mnist_data/',one_hot=True)
	
	Xtrain,Ytrain=mnist.train.next_batch(5000)    #限制训练样本的个数
	Xtest,Ytest=mnist.test.next_batch(200)      #测试样本的个数
	print('Xtrain.shape:',Xtrain.shape,'Xtest.shape:',Xtest.shape)
	print('Ytrain.shape:',Ytrain.shape,'Ytest.shape:',Ytest.shape)
	
	xtrain=tf.placeholder('float',[None,784],name='X_train')   #不知道训练样本的个数用None来表示，特证数是28*28=784
	xtest=tf.placeholder('float',[784],name='X_test')
	
	distance=tf.reduce_sum(tf.abs(tf.add(xtrain,tf.negative(xtest))),axis=1)  #逐行进行缩减运算，最终得到一个行向量
	
	pred=tf.arg_min(distance,0)   #获取最小距离的索引
	
	init=tf.global_variables_initializer()
	
	accuracy=0.
	
	with tf.Session() as sess:
	    sess.run(init)
	    Ntest=len(Xtest)  #测试样本数量
	
	    for i in range(Ntest):
	        nn_index=sess.run(pred,feed_dict={xtrain:Xtrain,xtest:Xtest[i,:]})   #每次只传入一个测试样本
	
	        pred_class_label=np.argmax(Ytrain[nn_index])
	        true_class_label=np.argmax(Ytest[i])
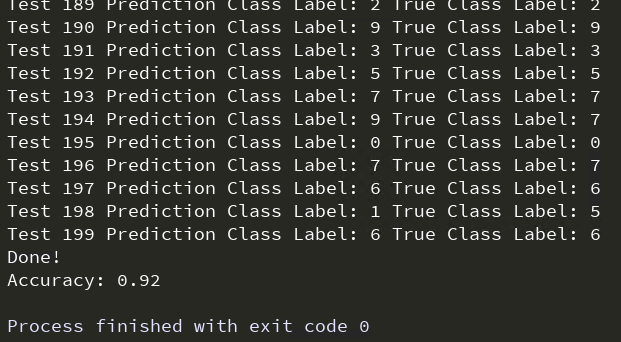
	        print('Test',i,'Prediction Class Label:',pred_class_label,'True Class Label:',true_class_label)
	
	        if pred_class_label==true_class_label:
	            accuracy+=1
	
	    print('Done!')
	    accuracy=accuracy/Ntest
	    print('Accuracy:',accuracy)
	
	
	writer=tf.summary.FileWriter(logdir='logs_KNN',graph=tf.get_default_graph())
	writer.flush()

得出最终训练结果，可以看到准确率是92%

最后

以上就是健壮哑铃为你收集整理的机器学习|TensorFlow实现KNN模型Tensorflow实现K近邻分类器的全部内容，希望文章能够帮你解决机器学习|TensorFlow实现KNN模型Tensorflow实现K近邻分类器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。