lecture 7：K近邻KNN

目录

1KNN思想

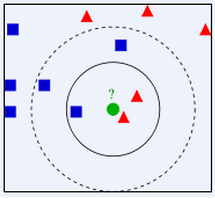
给定一个新样本，在已正确分类的样本集中，寻找与该样本最相似（距离最近）的K个样本，根据 K 个样本多数属类确定新样本的类别。

两个不足：
（1）当类样本数量不平衡时，容易造成新样本偏向样本数多的类，可以采用权值比例方法改进（与新样本距离小的邻居权值大）。

（2）计算量较大，要计算新样本到全体已知样本的距离，才能得到它的K个最近邻点。要事先对已知样本进行裁减，去除对分类作用不大的样本。

K的选择也直接影响到分类精度和实时性。

• KNN最重要的三个要素：距离度量、K的选择、分类决策规则

注意：
（1）计算量大，要剪枝
（2）变量要先标准化，不然会被更高范围的变量偏倚（数量级不平衡）
（3）要野值去除和噪音去除

• kNN靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的
  对类域的交叉或重叠较多的待分样本集来说，kNN方法较其他方法更为适合。

2距离函数

距离汇总：http://blog.sina.com.cn/s/blog_6f611c300101c5u2.html
距离函数种类：欧式距离、曼哈顿距离、明式距离（闵可夫斯基距离）、马氏距离、切比雪夫距离、标准化欧式距离、汉明距离、夹角余弦等

常用距离函数：欧式距离、马氏距离、曼哈顿距离、明式距离

欧式距离与马氏距离的比较

（1）欧式距离
最常见的两点之间或多点之间的距离表示法，又称之为欧几里得度量，它定义于欧几里得空间中，如点 x = (x1,…,xn) 和 y = (y1,…,yn) 之间的距离为：

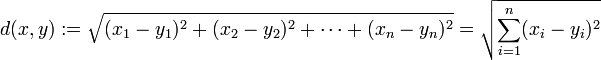
其上，二维平面上两点欧式距离，代码可以如下编写：

//unixfy：计算欧氏距离  
double euclideanDistance(const vector<</span>double>& v1, const vector<</span>double>& v2)  
{  
     assert(v1.size() == v2.size());  
     double ret = 0.0;  
     for (vector<</span>double>::size_type i = 0; i != v1.size(); ++i)  
     {  
         ret += (v1[i] - v2[i]) * (v1[i] - v2[i]);  
     }  
     return sqrt(ret);  
 }  

（2）马氏距离

3KNN模型

knn使用的模型实际上对应于对特征空间的划分，它有算法基本要素：
*距离度量
*K值选择
*分类决策规则

单元是指在特征空间中，对每个训练实例x，距离该点比其他点更近的所有点组成的一个区域。

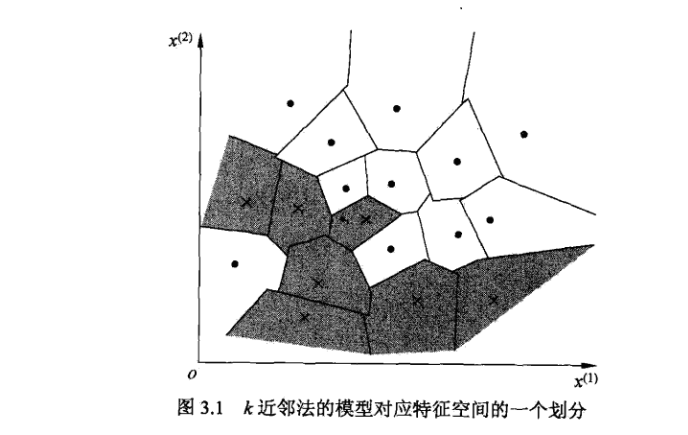
注意，为了简单起见，这里的图是二维的，当映射到多维空间时，我们就要使用一些手段进行降维，例如使用PCA简化数据，或者SVD矩阵分解，记住，数据的优化在机器学习方面尤其重要，即使你有个表现非常完美的算法，但当数据足够大并且掺杂着许多无用或者噪声数据时，数据优化是必须进行的

• K近邻法并不具有显式的学习过程,你必须先把数据集存下来，然后类似于比对的来作比较。K近邻法实际上是利用训练数据集对特征向量空间进行划分,并且作为其分类的模型

4K值的选择

（1）K较小，容易过拟合

当k值取得较小时，我们就在较小的邻域进行预测。显而易见，输入较近的实例对预测结果会产生良好的效果，也就是其学习的近似误差会减小。但这样会让结果对这个较小邻域中的点会非常敏感，也就是说其估计误差会变大，举个栗子，如果在这小范围的邻域内恰巧有一两个噪声数据，那么你的预测结果很可能会出错，这也就是我们在线性回归中的过拟合现象

（2）K较大，容易欠拟合

那么你可能要问，我把k值取得大一点，这样就可以避免噪声数据了吧！想法是好的，这样确实会减少学习的估计误差，但学习的近似误差会增大，也就是说较远的，相关性不强的点也会产生影响，这也就是我们在线性回归中的欠拟合现象

• 一般应用中，k取较小的数值，通常采用交叉验证法来选取最优的k值

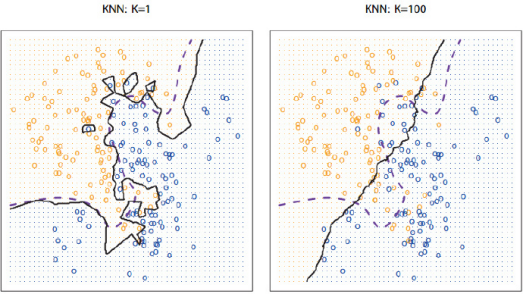
在上图中，紫色虚线是贝叶斯决策边界线，也是最理想的分类边界，黑色实线是KNN的分类边界。

可以发现：K越小，分类边界曲线越光滑，偏差越小，方差越大；K越大，分类边界曲线越平坦，偏差越大，方差越小。

所以即使简单如KNN，同样要考虑偏差和方差的权衡问题，表现为K的选取

5应用 scikit-learn 库实现k近邻算法

"""
scikit-learn 库对knn的支持
数据集是iris虹膜数据集
"""

from sklearn.datasets import load_iris  
from sklearn import neighbors  
import sklearn  

#查看iris数据集  
iris = load_iris()  
print(iris)

"""
KNeighborsClassifier(n_neighbors=5, weights='uniform', 
                     algorithm='auto', leaf_size=30, 
                     p=2, metric='minkowski', 
                     metric_params=None, n_jobs=1, **kwargs)

 n_neighbors: 默认值为5，表示查询k个最近邻的数目
 algorithm:   {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’},
              指定用于计算最近邻的算法，auto表示试图采用最适合的算法计算最近邻
 leaf_size:   传递给‘ball_tree’或‘kd_tree’的叶子大小
 metric:      用于树的距离度量。默认'minkowski与P = 2（即欧氏度量）
 n_jobs:      并行工作的数量，如果设为-1，则作业的数量被设置为CPU内核的数量
"""

knn = neighbors.KNeighborsClassifier()  

#训练数据集  
knn.fit(iris.data, iris.target)

#训练准确率
score = knn.score(iris.data, iris.target)

#预测
predict = knn.predict([[0.1,0.2,0.3,0.4]])

#预测，返回概率数组
predict2 = knn.predict_proba([[0.1,0.2,0.3,0.4]])

print(predict)
print(iris.target_names[predict])

score=0.966666667
predict=[0]

最后

以上就是独特百褶裙为你收集整理的机器学习总结（lecture 7）算法：K近邻KNNlecture 7：K近邻KNN目录的全部内容，希望文章能够帮你解决机器学习总结（lecture 7）算法：K近邻KNNlecture 7：K近邻KNN目录所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。