西瓜书第三章线性模型（概览）（未完。。。）

本章写作的大体思路：

首先作者线引出了线性模型的基本形式，

3.1基本形式

线性模型本质上来说就是希望学习出通过属性（x）的线性组合来进行表达预测值（可谓连续也可为离散）的函数。

若预测值离散：线性回归任务

若预测值离散：线性分类任务

线性模型的基本形式如下：

 3.2 线性回归

3.2.1 一元线性回归（最小二乘参数估计）

关于离散数据的连续化处理：若数据存在“序”的关系，那么可以通过数字赋值的方式将其连续化；如数据不存在“序”的关系，那么可以通过坐标表示来实现连续化。

首先一元线性回归的任务为：

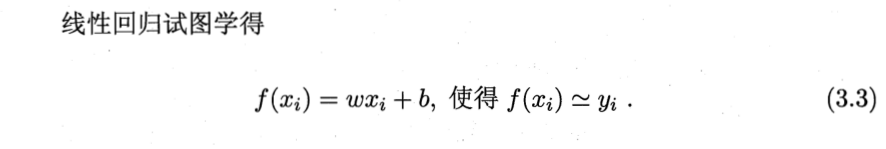
 其中xi、yi为已知量，通过xi、yi试图解出最好的w和b

怎么来衡量“最好的”呢？就是说预测值f(xi)与实际值yi的差别越小越好，于是我们可以用均方误差（欧式距离）来衡量，即：

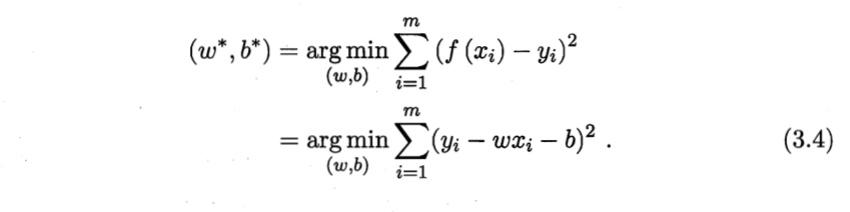
 于是我们的问题就转化为了求式（3.4），而对于求解（3.4）的基本思路就是式（3.4）对w和b分别求偏导，令其偏导数为零，就可以得到最好的w和b。（具体求解推导过程会在下一篇更）

3.2.2多元线性回归

一元线性回归只适合一个特征的情况下，这显然不能满足实际任务中有多个特征的情况，于是我们就引入了多元线性回归。

首先多元线性回归的任务为：

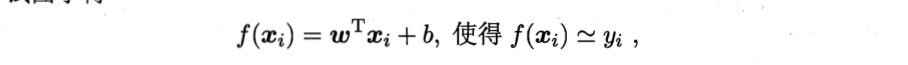
 其中xi（向量）、yi（向量）为已知量，通过xi（向量）、yi（向量）试图解出最好的wT（向量）

注意这里可以通过矩阵的向量化将b转移到wT（向量）中去。

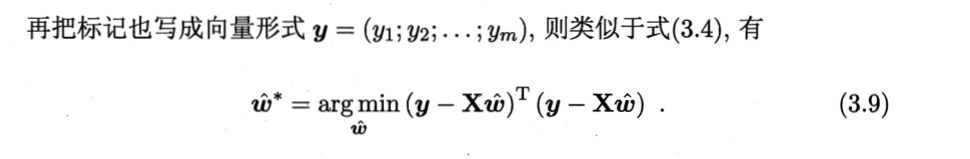
 求解思路与一元线性回归任务基本一致，式（3.9）对w*（向量）分别求偏导，令其偏导数为零，就可以得到最好的w*（向量）。（具体求解推导过程会在下一篇更）

3.2.3 广义线性回归

由于多元线性回归只能够学的线性函数映射不能学习非线性的模型，于是我们可以加入一个g(*)（单调可微），其基本形式：

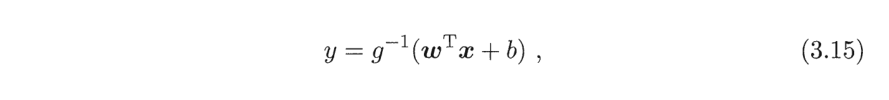
比如对数线性回归：

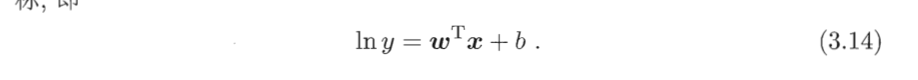
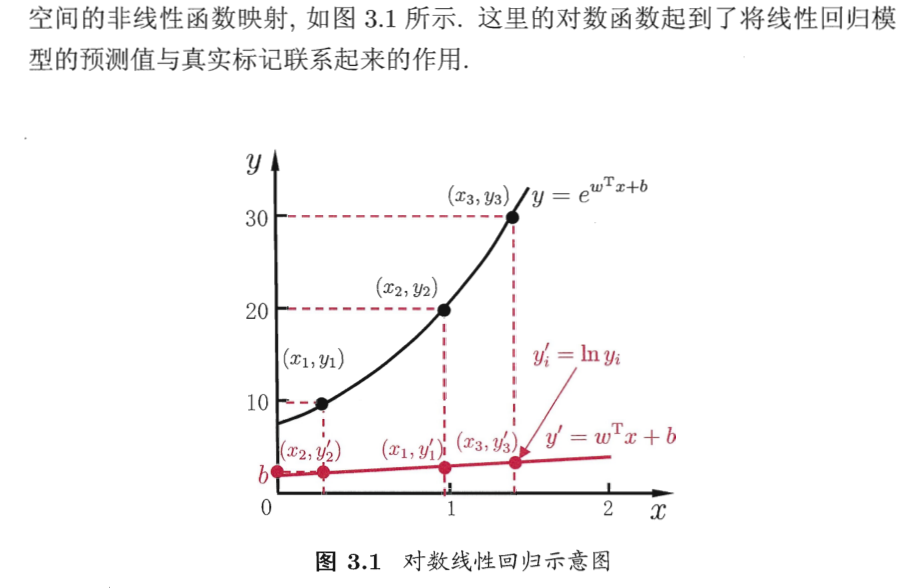
其中联系函数：起到将线性回归模型的预测值与实际值练习起来的作用

3.3 对数几率回归（逻辑回归）（分类）

对数几率回归也是广义线性回归的一个特例，在这里g(*)为：

 由于式（3.16）不连续因此不好求解，于是g(*)可以改为sigmoid函数：

 对式（3.18）进行恒等变形可以得到

 对于式（3.18）中w和b的求解：

 求解思路在这里只要是通过引入类后验概率和公式的恒等变形，然后引入极大似然估计法来求解（具体求解推导过程会在下一篇更）

3.4 线性判别分析（LDA）

LDA是一种经典的监督降维技术，他通过样本点投影的方式将样本维度降低了。

LDA的基本思想：在给定的训练样本集中，设法将样本点投影到一条直线上，然后利用类间方差大，类内方差小对样本进行分类。（具体求解推导过程会在下一篇更）

LDA也可以从贝叶斯的角度进行解释，并可证明，当两类数据同先验、满足高斯分布且协方差相等时，LDA可达到分类最优。

最后

以上就是彩色紫菜为你收集整理的西瓜书第三章线性模型（概览）（未完。。。）的全部内容，希望文章能够帮你解决西瓜书第三章线性模型（概览）（未完。。。）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。