西瓜书第三章线性模型学习目标：学习内容：学习时间：

77 阅读 0 评论 51 点赞

我是靠谱客的博主动听银耳汤，最近开发中收集的这篇文章主要介绍西瓜书第三章线性模型学习目标：学习内容：学习时间：，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

学习目标：

西瓜书第三章线性模型

学习内容：

`
本章讲了几种经典的线性模型，先从回归任务开始，然后讨论二分类问题。
1）基于均方误差最小化来进行模型求解的方法称为最小二乘法，在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的距离最小。广义线性模型的参数估计常通过加权最小二乘法或极大似然法进行。
2) 逻辑回归单位阶跃函数（Heavisde函数）y={0，z<0;0.5,z=0;1,z>0} 即若预测值z大于零就判为正例，小于零则判为反例，预测值为临界值则可任意判别。单位阶跃函数不连续，用逻辑函数替代，例如sigmoid tanh relu等不确定用哪个激活函数，在你的保留交叉验证数据集跑一跑或者开发集上跑一跑，看哪个参数好就用哪个。
3）极大似然似然就是likelihood，即可能性，取（μ=某具体值，…）的概率L越趋近于1（L越大），估计值（μ=某具体值，…）就越准确，即越接近真实概率分布（似然函数就是概率的乘积，似然函数越大时说明这些点在某个模型中概率越大，那就说明这个模型就是最接近真实分布的，那对应的参数自然就是目标参数）
4） LDA可从贝叶斯决策理论的角度来阐述，并可证明，当两类数据同先验，满足高斯分布且协方差相等时，LDA可达到最优分类。
5）多分类学习一般而言，利用二分类学习器来解决多分类问题。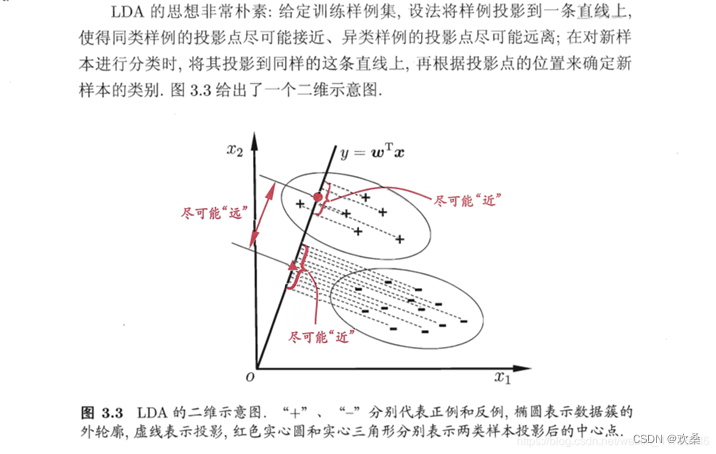在这里插入图片描述

实际上LDA除了可以用于降维以外，还可以用于分类。一个常见的LDA分类基本思想是假设各个类别的样本数据符合高斯分布，这样利用LDA进行投影后，可以利用极大似然估计计算各个类别投影数据的均值和方差，进而得到该类别高斯分布的概率密度函数。当一个新的样本到来后，我们可以将它投影，然后将投影后的样本特征分别带入各个类别的高斯分布概率密度函数，计算它属于这个类别的概率，最大的概率对应的类别即为预测类别。
6）OvO将N个类别两两配对，从而产生N(N-1)/2个二分类任务，最终结果可通过投票，即把被预测的最多的类别作为最终分类结果；OvR 则是每次讲一个类的样例作为正例，其他所有的样例作为反例来训练N个分类器，若有多个分类器测为正类，则通常考虑分类器的预测置信度，选择置信度最大的类别标记为分类结果，只需要N个分类器；MvM是每次将若干个类作为正类，若干个其他类作为反类，最常用的MvM技术叫纠错输出码（ECOC）,ECOC分为两步：编码，解码。
7）类别不平衡就是指分类任务中不同类别的训练样例数目差别很大的情况。Y/(1-y)反映了正例与反例可能性之比值，分类器决策规则为该值大于1则为正例。