我是
靠谱客的博主
文艺小蝴蝶,这篇文章主要介绍
机器学习-周志华-课后习题答案-线性模型,现在分享给大家,希望可以做个参考。
3.1试分析在什么情况下,在以下式子中不比考虑偏置项b。

答:在线性回归中,所有参数的确定都是为了让残差项的均值为0且残差项的平方和最小。在所有其他参数项确定后,偏置项b(或者说是常数项)的变化体现出来的就是拟合曲线的上下整体浮动,可以看做是其他各个解释变量留下的bias的线性修正。因此在线性拟合过程中是需要考虑偏置项的。
但若需要做的是比较不同自变量对因变量的影响,那么不需要考虑常数项,这样得到的回归系数是标准化的回归系数。
3.2试证明,对于参数w,对率回归(logistics回归)的目标函数(式1)是非凸的,但其对数似然函数(式2)是凸的。

3.3编程实现对率回归,并给出西瓜数据集3.0α上的结果
西瓜数据集3.0α:
编号 | 密度 | 含糖率 | 好瓜 |
1 | 0.697 | 0.46 | 是 |
2 | 0.774 | 0.376 | 是 |
3 | 0.634 | 0.264 | 是 |
4 | 0.608 | 0.318 | 是 |
5 | 0.556 | 0.215 | 是 |
6 | 0.403 | 0.237 | 是 |
7 | 0.481 | 0.149 | 是 |
8 | 0.437 | 0.211 | 是 |
9 | 0.666 | 0.091 | 否 |
10 | 0.243 | 0.0267 | 否 |
11 | 0.245 | 0.057 | 否 |
12 | 0.343 | 0.099 | 否 |
13 | 0.639 | 0.161 | 否 |
14 | 0.657 | 0.198 | 否 |
15 | 0.36 | 0.37 | 否 |
16 | 0.593 | 0.042 | 否 |
17 | 0.719 | 0.103 | 否 |
答:
首先将数据存入excel表,存为csv格式。再将是/否 转为1/0
参考《机器学习实战》的内容。本题分别写了梯度上升方法以及随机梯度上升方法。对书本上的程序做了一点点改动
-
- from numpy import *
- import pandas as pd
- import matplotlib.pyplot as plt
-
-
- df=pd.read_csv('watermelon_3a.csv')
- m,n=shape(df.values)
- df['norm']=ones((m,1))
- dataMat=array(df[['norm','density','ratio_sugar']].values[:,:])
- labelMat=mat(df['label'].values[:]).transpose()
-
-
- def sigmoid(inX):
- return 1.0/(1+exp(-inX))
-
-
- def gradAscent(dataMat,labelMat):
- m,n=shape(dataMat)
- alpha=0.1
- maxCycles=500
- weights=array(ones((n,1)))
-
- for k in range(maxCycles):
- a=dot(dataMat,weights)
- h=sigmoid(a)
- error=(labelMat-h)
- weights=weights+alpha*dot(dataMat.transpose(),error)
- return weights
-
-
- def randomgradAscent(dataMat,label,numIter=50):
- m,n=shape(dataMat)
- weights=ones(n)
- for j in range(numIter):
- dataIndex=range(m)
- for i in range(m):
- alpha=40/(1.0+j+i)+0.2
-
- randIndex_Index=int(random.uniform(0,len(dataIndex)))
- randIndex=dataIndex[randIndex_Index]
- h=sigmoid(sum(dot(dataMat[randIndex],weights)))
- error=(label[randIndex]-h)
- weights=weights+alpha*error[0,0]*(dataMat[randIndex].transpose())
- del(dataIndex[randIndex_Index])
- return weights
-
-
- def plotBestFit(weights):
- m=shape(dataMat)[0]
- xcord1=[]
- ycord1=[]
- xcord2=[]
- ycord2=[]
- for i in range(m):
- if labelMat[i]==1:
- xcord1.append(dataMat[i,1])
- ycord1.append(dataMat[i,2])
- else:
- xcord2.append(dataMat[i,1])
- ycord2.append(dataMat[i,2])
- plt.figure(1)
- ax=plt.subplot(111)
- ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
- ax.scatter(xcord2,ycord2,s=30,c='green')
- x=arange(0.2,0.8,0.1)
- y=array((-weights[0]-weights[1]*x)/weights[2])
- print shape(x)
- print shape(y)
- plt.sca(ax)
- plt.plot(x,y)
-
- plt.xlabel('density')
- plt.ylabel('ratio_sugar')
-
- plt.title('ramdom gradAscent logistic regression')
- plt.show()
-
-
- weights=randomgradAscent(dataMat,labelMat)
- plotBestFit(weights)
梯度上升法得到的结果如下:
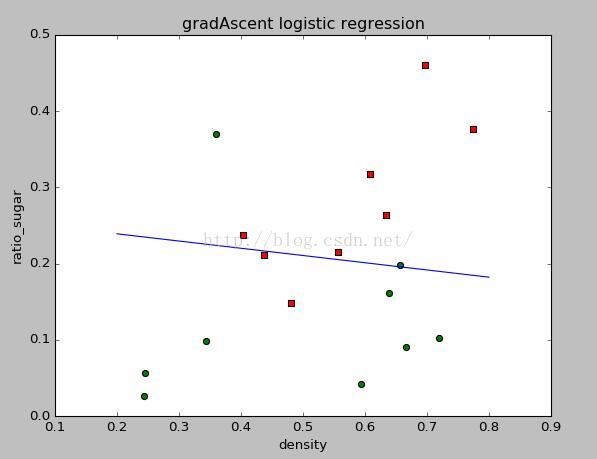
随机梯度上升法得到的结果如下:

可以看出,两种方法的效果基本差不多。但是随机梯度上升方法所需要的迭代次数要少很多。
3.4选择两个UCI数据集,比较10折交叉验证法和留一法所估计出的对率回归的错误率。
(UCI数据集: archive.ics.uci.edu/ml/)
答:嫌麻烦所以没弄。有兴趣可以把数据下下来跑跑看
另外可以直接用sklearn做cv。更加方便
3.5 编程实现线性判别分析,并给出西瓜数据集3.0α上的结果
答:
LDA的编程主要参考书上P62的3.39 以及P61的3.33这两个式子。由于用公式可以直接算出,因此比较简单
代码如下:
-
- from numpy import *
- import numpy as np
- import pandas as pd
- import matplotlib.pyplot as plt
-
- df=pd.read_csv('watermelon_3a.csv')
-
- def calulate_w():
- df1=df[df.label==1]
- df2=df[df.label==0]
- X1=df1.values[:,1:3]
- X0=df2.values[:,1:3]
- mean1=array([mean(X1[:,0]),mean(X1[:,1])])
- mean0=array([mean(X0[:,0]),mean(X0[:,1])])
- m1=shape(X1)[0]
- sw=zeros(shape=(2,2))
- for i in range(m1):
- xsmean=mat(X1[i,:]-mean1)
- sw+=xsmean.transpose()*xsmean
- m0=shape(X0)[0]
- for i in range(m0):
- xsmean=mat(X0[i,:]-mean0)
- sw+=xsmean.transpose()*xsmean
- w=(mean0-mean1)*(mat(sw).I)
- return w
-
- def plot(w):
- dataMat=array(df[['density','ratio_sugar']].values[:,:])
- labelMat=mat(df['label'].values[:]).transpose()
- m=shape(dataMat)[0]
- xcord1=[]
- ycord1=[]
- xcord2=[]
- ycord2=[]
- for i in range(m):
- if labelMat[i]==1:
- xcord1.append(dataMat[i,0])
- ycord1.append(dataMat[i,1])
- else:
- xcord2.append(dataMat[i,0])
- ycord2.append(dataMat[i,1])
- plt.figure(1)
- ax=plt.subplot(111)
- ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
- ax.scatter(xcord2,ycord2,s=30,c='green')
- x=arange(-0.2,0.8,0.1)
- y=array((-w[0,0]*x)/w[0,1])
- print shape(x)
- print shape(y)
- plt.sca(ax)
-
- plt.plot(x,y)
- plt.xlabel('density')
- plt.ylabel('ratio_sugar')
- plt.title('LDA')
- plt.show()
-
- w=calulate_w()
- plot(w)
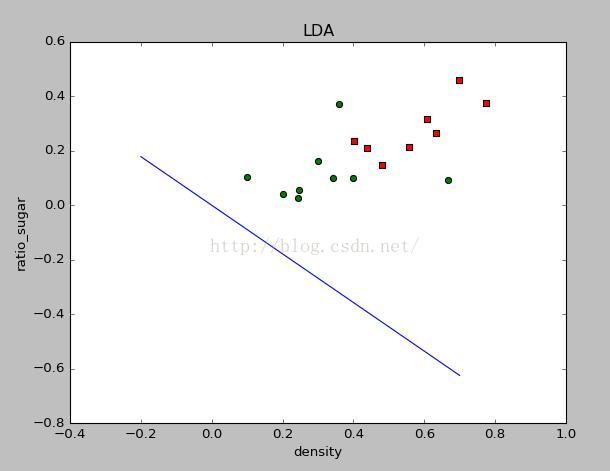
结果如下:

对应的w值为:
[ -6.62487509e-04, -9.36728168e-01]
由于数据分布的关系,所以LDA的效果不太明显。所以我改了几个label=0的样例的数值,重新运行程序得到结果如下:
效果比较明显,对应的w值为:
[-0.60311161, -0.67601433]
3.6 LDA仅在线性可分数据上能获得理想结果,试设计一个改进方法,使其能较好地用于非线性可分数据
答:
利用核方法即可以将LDA用于非线性可分数据,即KLDA(核线性判别分析方法)。见教材的P137
3.7令码长为9,类别数为4,试给出海明距离意义下理论最优的EOOC二元码并证明之。
答:
关于EOOC编码,我没有在网上找到什么资料。。所以按照自己的理解给出一个结果。不知道是否是理论最优。
类别数为4,因此1V3有四种分法,2V2有六种分法,3V1同样有四种分法。按照书上的话,理论上任意两个类别之间的距离越远,则纠错能力越强。那么可以等同于让各个类别之间的累积距离最大。对于1个2V2分类器,4个类别的海明距离累积为4;对于3V1与1V3分类器,海明距离均为3,因此认为2V2的效果更好。因此我给出的码长为9,类别数为4的最优EOOC二元码由6个2V2分类器和3个3v1或1v3分类器构成。
3.8* EOOC编码能起到理想纠错作用的重要条件是:在每一位编码上出错的概率相当且独立。试析多分类任务经ECOC编码后产生的二类分类器满足该条件的可能性及由此产生的影响。
答:
(个人理解,若有错误或不同理解烦请指出)在每一位编码上出错的概率即指在第i个分类器上的错误率,假设每个分类器选择相同的模型与最优的参数。那么满足概率相当并且独立应该需要每个分类器的正负例比例相当,并且每个分类器划分的正负例在空间中的相对分布情况应当相近。一般情况下一般很难满足这样的条件,肯定会有错误率较高的分类器。错误率较高的分类器在较少时影响不大,但当高错误率分类器占到多数时,就会拖低整体的错误率。所以我认为在某些极端情况下,增加码长可能会降低正确率
3.9使用OvR和MvM将多分类任务分解为二分类任务求解时,试述为何无需专门针对类别不平衡性进行处理。
答:
因为OvR或者MvM在输出结果阶段,是对各个二分类器的结果进行汇总,汇总的这个过程就会消除不平衡带来的影响(因为总和总是1)
3.10*试推导出多分类代价敏感学习(仅考虑基于类别的误分类代价)使用“再缩放“能获得理论最优解的条件。
最后
以上就是文艺小蝴蝶最近收集整理的关于机器学习-周志华-课后习题答案-线性模型的全部内容,更多相关机器学习-周志华-课后习题答案-线性模型内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。












![[西瓜书]——第三章部分编程答案](https://file2.kaopuke.com:8081/files_image/reation/bcimg12.png)
![matlab中bilinear函数,【Bilinear interpolation】双线性插值详解(转)[组图]](https://file2.kaopuke.com:8081/files_image/reation/bcimg13.png)
发表评论 取消回复