西瓜书《机器学习》课后答案——Chapter3_3.5

编程实现线性判别分析，并给出西瓜数据集3.0alpha上的结果。

"""
Author: Victoria
Created on: 2017.9.15 11:45
"""
import xlrd
import numpy as np
import matplotlib.pyplot as plt

def LDA(X0, X1):
    """
    Get the optimal params of LDA model given training data.
    Input:
        X0: np.array with shape [N1, d]
        X1: np.array with shape [N2, d]
    Return:
        omega: np.array with shape [1, d]. Optimal params of LDA.
    """
    #shape [1, d]
    mean0 = np.mean(X0, axis=0, keepdims=True)
    mean1 = np.mean(X1, axis=0, keepdims=True)
    Sw = (X0-mean0).T.dot(X0-mean0) + (X1-mean1).T.dot(X1-mean1)
    omega = np.linalg.inv(Sw).dot((mean0-mean1).T)
    return omega

if __name__=="__main__":
    #read data from xls
    work_book = xlrd.open_workbook("3.0alpha.xlsx")
    sheet = work_book.sheet_by_name("Sheet1")
    x1 = sheet.row_values(0)
    x2 = sheet.row_values(1)
    p_x1 = x1[0:8]
    p_x2 = x2[0:8]
    n_x1 = x1[8:]
    n_x2 = x2[8:]
    X0 = np.vstack([n_x1, n_x2]).T
    X1 = np.vstack([p_x1, p_x2]).T
    print X0

    #LDA
    omega = LDA(X0, X1)

    #plot
    plt.plot(p_x1, p_x2, "bo")
    plt.plot(n_x1, n_x2, "r+")
    lda_left = 0
    lda_right = -(omega[0]*0.9) / omega[1]
    plt.plot([0, 0.9], [lda_left, lda_right], 'g-')

    plt.xlabel('density')
    plt.ylabel('sugar rate')
    plt.title("LDA")
    plt.show()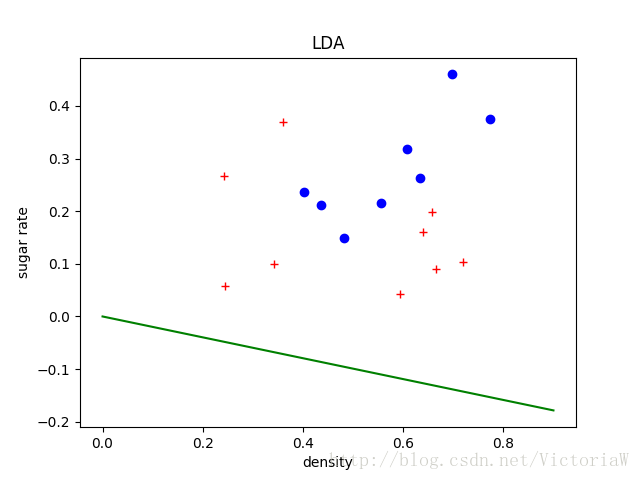

$y=boldsymbol omega^T boldsymbol x$得到的是投影点到原点的距离。经过此变换之后，相当于把二维数据降维到一维数据。

最后

以上就是唠叨含羞草为你收集整理的西瓜书《机器学习》课后答案——Chapter3_3.5的全部内容，希望文章能够帮你解决西瓜书《机器学习》课后答案——Chapter3_3.5所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。