机器学习-学习笔记（三）第三章 线性模型

线性模型试图通过一个属性的线性组合来得到一个预测值进行预测，即

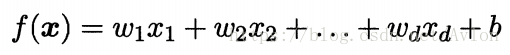
或者可以写成矩阵形式，即

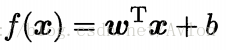
其中和b通过学习得到，线性模型非常容易理解，他通过对所有属性进行综合考虑来进行预测，其中权值可以理解为某个属性的重要程度，例如在判断苹果是否成熟的问题上，表皮的颜色就是很重要的判断依据，而相对来说苹果的形状可能没有那么重要，在模型中则反映在权值的大小上。线性模型也是许多复杂模型的基础，理解线性模型有助于后续的学习，下面介绍几种经典的线性模型。

线性回归（linear regression）

线性回归试图用上面所说的线性模型一般形式来预测输出，通过“最小二乘法”即使得预测输出与真是标记的均方差最小来确定和b的值。首先来讨论简单的输入形式，假设数据集,其中。首先我们讨论较为简单的情况，令d=1，即只有一个属性的输入，对于离散的属性若属性存在“序”，可通过连续化将其转化为连续值，例如“身高”的取值“高”、“矮”转化为{1，0}，若不存在序的关系的有k个取值的属性，则转化为k维向量如（1，0，0）、（0，1，0）的形式。

最小二乘法中的关键是均方差函数，对于上述输入我们定义均方差函数,我们对和b求偏导，得到和，令两个偏导为0，可得到和b的解。

当数据集D的样本由d个属性描述的时候，称为多元线性回归（multivariate linear regression）将我们的回归方程用矩阵表示,一样使用最小二乘法进行参数估计，这里涉及对矩阵的求导运算，当我们希望预测y的衍生物时，则模型就是广义线性模型，形如,其中g()为单调可微函数。

对数几率回归

用对数几率函数替代单位阶跃函数后便可得到对数几率回归模型，将代入广义线性模型的中也可以得到这个模型，得到，将y视为样本x作为正例的可能性，1-y是其反例可能性，两者比值称为几率。根据上面说的概率我们将等式改写成

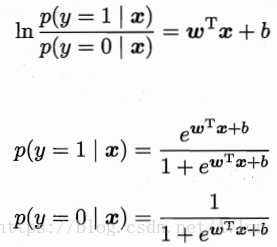
用最大似然法来估计和b，具体不再展开。

线性判别分析（Linear Discriminant Analysis）

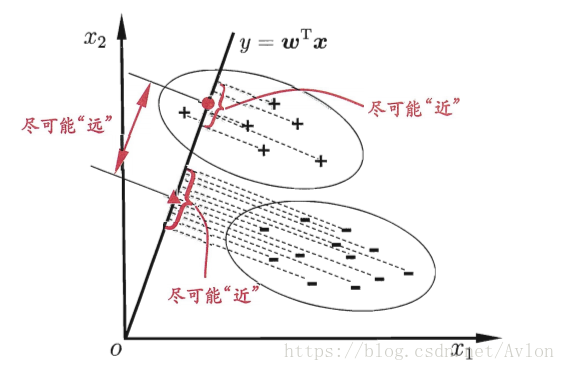
其算法思想就是选取一条合适的直线，将所有的样本点投影到该直线上，令同类样本的投影点尽可能近，不同类样本的投影点尽可能远，令、、分别表示第i类示例的集合、均值向量、协方差矩阵，将数据投影到直线上，则两类样本的中心在直线上的投影分别为和，两类样本的协方差分别是和，为了达成上述目的，使+尽可能小，尽可能大，定义几个量

类内散度矩阵

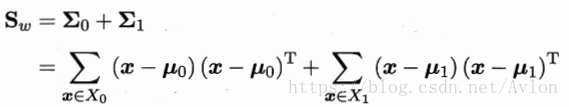
类间散度矩阵

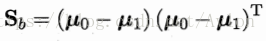
LDA欲最大化目标

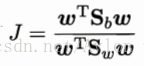
由拉格朗日乘子法可以确定参数，在解方程中要用到奇异值分解，这里不展开讨论，LDA可以很容易的推广到多分类任务中，基本思想与二分类任务相同，最优化目标有很多种。

多分类任务，几种基本思路就是用二分类的组合策略去实现多分类任务，包括OvO（一对一）、OvR（一对多）、MvM（多对多），其中OvO（一对一）、OvR（一对多）一般采用多数投票制，而MvM的正反例都得特殊构造，例如纠错输出码。

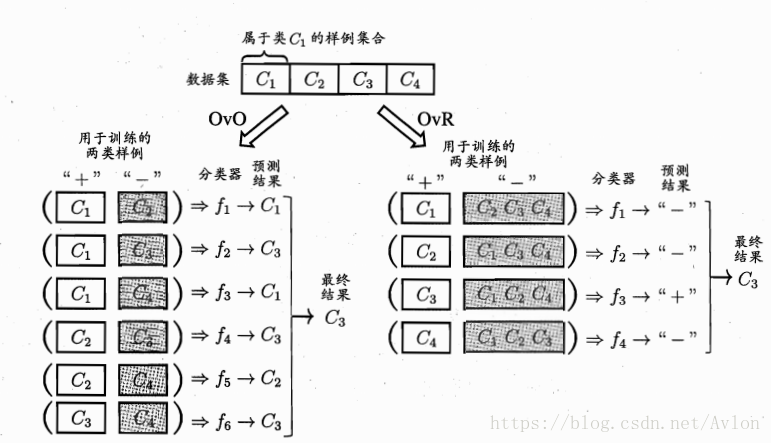
上图左边是OvO模型，右边是OvR模型。

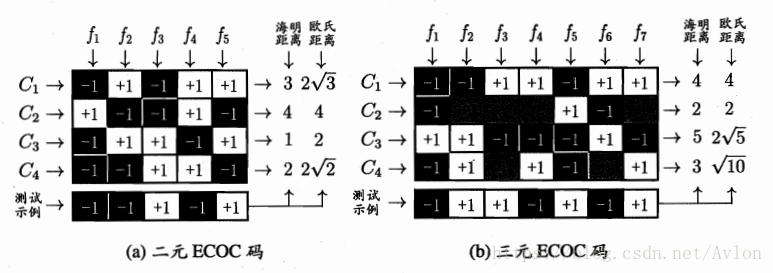
ECOC（纠错输出码）中选取与测试示例距离最近的类别作为输出，具有一定的纠错能力。

第三章习题待续

最后

以上就是自信羽毛为你收集整理的机器学习-学习笔记（三）第三章 线性模型的全部内容，希望文章能够帮你解决机器学习-学习笔记（三）第三章 线性模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。