3.3 对数几率回归

针对二分类的分类模型中

给出$x$希望模型得到的$f(x)$代表正样本的概率

线性回归：$f(x)\in R$

分类回归：$f(x)\in [0,1]$

分类任务下使用线性回归

• 可以使用单调可微函数将分类任务的真实标记$y$与线性回归模型的预测值联系起来
• 例，可使用单位阶跃函数
• 相当于给线性回归的函数套了一个映射函数

单位阶跃函数

Heaviside函数

例：

$$y=\{\begin{array}{cc}0,& z<0\\ 0.5,& z=0\\ 1,& z>0\end{array}$$

在这种情况下，若预测值$z$大于0就判定为正例，小于0就判定为反例，预测值为临界值0则可以任意判别

存在的问题：单位阶跃函数不连续，不能直接使用$g^{-}(\cdot )$

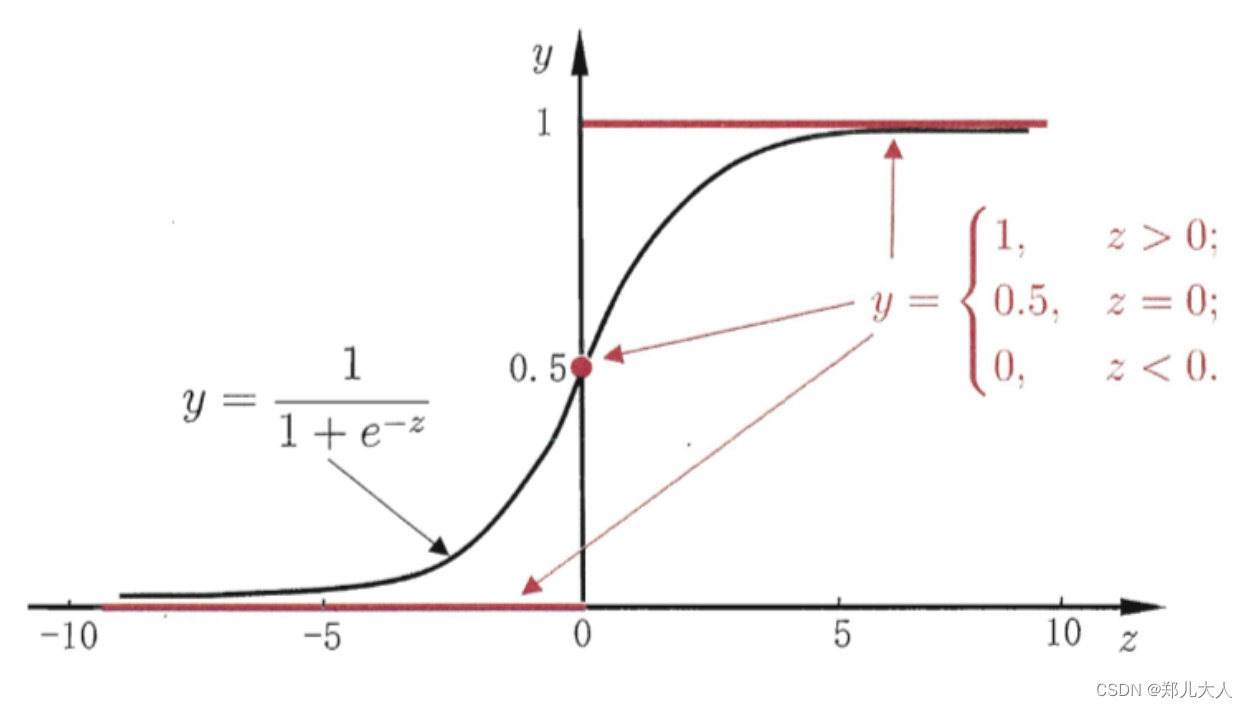
对数几率函数

logistic function

简称”对率函数"

$$y=\frac{1}{1+e^{-z}}$$

$$y=\frac{1}{1+e^{-\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right)}}$$

特点

• 单调可微
• 一定程度上近似单位阶跃函数
• 一种"Sigmoid"函数
  • 形似S的函数
  • 对率函数是Sigmoid函数的重要代表
• 严格是取不到0，1的

对数几率函数原理

1）对数几率

将对数几率函数进一步变形

$$\ln \frac{y}{1-y}={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$

其中$y$视为样本$x$为正例的可能性，$y-1$为反例的可能性，则二者的比值称为几率：

$$\frac{y}{1-y}$$

• “几率” ( odds ) 反映了$x$作为正例的相对可能性
• 将几率取对数得到的称为"对数几率" (log odds, logit)
  • $\ln \frac{y}{1-y}$

所以实际上这个过程是用线性回归模型的预测结果去逼近真实标记的对数几率

故对应的模型称为**“对数几率回归”(logistic regression, logit regression)**

• 虽然名称是回归，但是做的是回归算法
• 有的文献中译为逻辑回归

2）最大熵原理

对数几率函数的优点

• 直接对分类可能性进行建模，无需事先假设数据分布
• 得到了近似概率的预测，既包含了类别信息，又可以辅助利用概率进行决策的任务
• 很好的数学性质，有任意阶可导的凸函数

单位阶跃函数 v.s. 对数几率函数

损失函数的推导

极大似然估计角度

步骤

• 确定概率密度质量函数
• 写出似然函数

概率密度函数

针对不同样本，真实标记有两种情况0和1

在给定$x$的情况下，模型针对$y=1$和$y=0$的预测概率结果分别为：

$$\begin{array}{l}p(y=1\mid \mathbf{x})=\frac{1}{1+e^{-\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right)}}=\frac{e^{{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b}}{1+e^{{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b}}\\ p(y=0\mid \mathbf{x})=1-p(y=1\mid \mathbf{x})=\frac{1}{1+e^{{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b}}\end{array}$$

对式子进行化简，$\mathbf{\beta }=(\mathbf{w};b),\hat{\mathbf{x}}=(\mathbf{x};1)$，得到结果

$$\begin{array}{l}p(y=1\mid \hat{\mathbf{x}};\mathbf{\beta })=\frac{e^{{\mathbf{\beta }}^{\mathrm{T}}\hat{\mathbf{x}}}}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}\hat{\mathbf{x}}}}=p_1(\hat{\mathbf{x}};\mathbf{\beta })\\ p(y=0\mid \hat{\mathbf{x}};\mathbf{\beta })=\frac{1}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}\hat{\mathbf{x}}}}=p_0(\hat{\mathbf{x}};\mathbf{\beta })\end{array}$$

由于我们只关心预测真实标记的概率情况，所以针对单个样本的概率质量函数为：

$$p(y\mid \hat{\mathbf{x}};\mathbf{\beta })=y\cdot p_1(\hat{\mathbf{x}};\mathbf{\beta })+(1-y)\cdot p_0(\hat{\mathbf{x}};\mathbf{\beta })$$

或者

$$p(y\mid \hat{\mathbf{x}};\mathbf{\beta })={\left[p_1(\hat{\mathbf{x}};\mathbf{\beta })\right]}^y{\left[p_0(\hat{\mathbf{x}};\mathbf{\beta })\right]}^{1-y}$$

似然函数

考虑$m$的样本

$$L(\mathbf{\beta })=\prod _{i=1}^{m}p\left(y_i\mid {\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)$$

将似然函数进行转换

$$\begin{array}{c}\ell (\mathbf{\beta })=\ln L(\mathbf{\beta })={\sum }_{i=1}^m\ln p\left(y_i\mid {\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)\\ \ell (\mathbf{\beta })={\sum }_{i=1}^m\ln \left(y_i{p}_1\left({\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)+\left(1-y_i\right)p_0\left({\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)\right)\end{array}$$
将 $p_1\left({\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)=\frac{e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}},p_0\left({\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)=\frac{1}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}}$代入上式可得
$$\begin{array}{l}\ell (\mathbf{\beta })={\sum }_{i=1}^m\ln \left(\frac{y_i{e}^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}}+\frac{1-y_i}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}}{\hat{\mathbf{x}}}_i}\right)\\ ={\sum }_{i=1}^m\ln \left(\frac{y_i{e}^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}+1-y_i}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}}{\hat{\mathbf{x}}}_i}\right)\\ ={\sum }_{i=1}^m\left(\ln \left(y_i{e}^{{\beta }^{\mathrm{T}}{\hat{\mathbf{x}}}_i}+1-y_i\right)-\ln \left(1+e^{{\beta }^{\mathrm{T}}{\hat{\mathbf{x}}}_i}\right)\right)\end{array}$$

将$y_i$等于1或者0代入，得到

$$\ell (\mathbf{\beta })=\{\begin{array}{ll}{\sum }_{i=1}^m\left(-\ln \left(1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}\right)\right),& y_i=0\\ {\sum }_{i=1}^m\left({\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i-\ln \left(1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}\right)\right),& y_i=1\end{array}$$

将两个式子进行综合得到

$$\ell (\mathbf{\beta })=\sum _{i=1}^m\left(y_i{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i-\ln \left(1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}\right)\right)$$

通常损失函数是以最小化为优化目标

所以可以将式子取相反数，得到损失函数的优化目标为

$$\ell (\mathbf{\beta })=-\sum _{i=1}^m\left(y_i{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i-\ln \left(1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}\right)\right)$$

信息论角度

自信息

$$I(X)=-{\log }_{b}p(x)$$

当$b=2$时单位为bit，当$b=e$时单位为nat

信息熵

$$H(X)=E[I(X)]=-\sum _{x}p(x){\log }_{b}p(x)$$

(离散型信息熵)

自信息的期望

度量随机变量$X$的不确定性，信息熵越大越不确定

约定：若$p(x)=0$，则 $p(x){\log }_{b}p(x)=0$

相对熵 ( KL散度 )

$$\begin{array}{rl}{D}_{KL}(p\Vert q)& =\sum _{x}p(x){\log }_b\left(\frac{p(x)}{q(x)}\right)\\ & =\sum _{x}p(x)\left({\log }_{b}p(x)-{\log }_{b}q(x)\right)\\ & =\sum _{x}p(x){\log }_{b}p(x)-\sum _{x}p(x){\log }_{b}q(x)\end{array}$$

其中$-{\sum }_{x}p(x){\log }_{b}q(x)$称为交叉熵

求和的含义是遍历$x$所有的值

度量两个分布的差异

典型使用场景，度量理想分布$p(x)$和模拟分布$q(x)$之间的差异

优化原理

• 理想分布最接近的模拟分布即为最优分布
• 因此可以通过最小化相对熵这个策略来求出最优分布
• 理想分布$p(x)$是未知但固定，所以${\sum }_{x}p(x){\log }_{b}p(x)$为常量
• 最小化相对熵就等价于最小化交叉熵

以对数几率回归为例，对单个样本$y_i$来说，它的理想分布是

$$p\left(y_i\right)=\{\begin{array}{ll}p(1)=1,p(0)=0,& y_i=1\\ p(1)=0,p(0)=1,& y_i=0\end{array}$$

现在模型的模拟分布是

$$q\left(y_i\right)=\{\begin{array}{ll}\frac{e^{{\beta }^{\mathrm{T}}\hat{x}}}{1+e^{{\beta }^{\mathrm{T}}\hat{x}}}=p_1(\hat{\mathbf{x}};\mathbf{\beta }),& y_i=1\\ \frac{1}{1+e^{{\beta }^{\mathrm{T}}}}=p_0(\hat{\mathbf{x}};\mathbf{\beta }),& y_i=0\end{array}$$

对于单个样本$y_i$的交叉熵为

$$-\sum _{y_i}p\left(y_i\right){\log }_{b}q\left(y_i\right)$$

将模型的预测结果进行代入

$$-p(1)\cdot {\log }_b{p}_1(\hat{\mathbf{x}};\mathbf{\beta })-p(0)\cdot {\log }_b{p}_0(\hat{\mathbf{x}};\mathbf{\beta })$$

同时令$b=e$

$$-y_i\ln p_1(\hat{\mathbf{x}};\mathbf{\beta })-\left(1-y_i\right)\ln p_0(\hat{\mathbf{x}};\mathbf{\beta })$$

全体训练样本的交叉熵为

⁡ ∑ i = 1 m [ − y i ln ⁡ p 1 ( x ^ i ; β ) − ( 1 − y i ) ln ⁡ p 0 ( x ^ i ; β ) ] ∑ i = 1 m { − y i [ ln ⁡ p 1 ( x ^ i ; β ) − ln ⁡ p 0 ( x ^ i ; β ) ] − ln ⁡ ( p 0 ( x ^ i ; β ) ) } ∑ i = 1 m [ − y i ln ⁡ ( p 1 ( x ^ i ; β ) p 0 ( x ^ i ; β ) ) − ln ⁡ ( p 0 ( x ^ i ; β ) ) ] begin{aligned} operatorname{} & sum_{i=1}^{m}left[-y_{i} ln p_{1}left(hat{boldsymbol{x}}_{i} ; boldsymbol{beta}right)-left(1-y_{i}right) ln p_{0}left(hat{boldsymbol{x}}_{i} ; boldsymbol{beta}right)right] \ &sum_{i=1}^{m}left{-y_{i}left[ln p_{1}left(hat{boldsymbol{x}}_{i} ; boldsymbol{beta}right)-ln p_{0}left(hat{boldsymbol{x}}_{i} ; boldsymbol{beta}right)right]-ln left(p_{0}left(hat{boldsymbol{x}}_{i} ; boldsymbol{beta}right)right)right} \ & sum_{i=1}^{m}left[-y_{i} ln left(frac{p_{1}left(hat{boldsymbol{x}}_{i} ; boldsymbol{beta}right)}{p_{0}left(hat{boldsymbol{x}}_{i} ; boldsymbol{beta}right)}right)-ln left(p_{0}left(hat{boldsymbol{x}}_{i} ; boldsymbol{beta}right)right)right] \ end{aligned} ​i=1∑m​[−yi​lnp1​(x^i​;β)−(1−yi​)lnp0​(x^i​;β)]i=1∑m​{−yi​[lnp1​(x^i​;β)−lnp0​(x^i​;β)]−ln(p0​(x^i​;β))}i=1∑m​[−yi​ln(p0​(x^i​;β)p1​(x^i​;β)​)−ln(p0​(x^i​;β))]​

将具体的式子代入后得到

$$\sum _{i=1}^m\left[-y_i\ln \left(\frac{\frac{e^{{\beta }^{\mathrm{T}}\hat{\mathbf{x}}}}{1+e^{{\beta }^{\mathrm{T}}\hat{\mathbf{x}}}}}{\frac{1}{1+e^{{\beta }^{\mathrm{T}}\hat{x}}}}\right)-\ln \left(\frac{1}{1+e^{{\mathbf{\beta }}^{\mathrm{T}}\hat{\mathbf{x}}}}\right)\right]$$

经整理后得到

$$\sum _{i=1}^m\left(-y_i{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i+\ln \left(1+e^{{\mathbf{\beta }}^{\mathrm{T}}{\hat{\mathbf{x}}}_i}\right)\right)$$

可以发现这两种角度下得到的损失函数结果是相同的

3.4 线性判别分析

Linear Discriminant Analysis ( LDA )

LDA思想

• 将样例投射到一条直线上
• 样例之间的关系
  • 同类样例的投影点尽可能接近
  • 异类样例的投影点尽可能远离
• 对于新样本进行分类时，投射到同样的直线上，根据投影点位置确定新样本的类别

线性判别分析 v.s. Fisher判别分析

在分类问题上，Fisher判别分析更早提出

LDA假设了各类样本的协方差矩阵相同且满秩

LDA的形式化表述

$X_i$其中$X_0$，$X_1$分别代表所有的负样本和正样本

${\mu }_0$和${\mu }_1$分别代表负样本和正样本的均值

${\sum }_0$和${\sum }_1$分别代表负样本和正样本的方差

$$\begin{gathered} {\sum }_i={\sum }_{x \\ \in X_i}(x-{\mu }_i)(x-{\mu }_i{)}^T \end{gathered}$$

在式子的表示中省略掉了$\frac{1}{m_i}$，但是这个系数并不影响LDA的结果

求解$w$向量的时候，为什么只关注于方向而不关心大小

以均值${\mu }_0$和${\mu }_1$为例，利用模型得到的$y$值本质上是均值对直线的投影

$y=|\mu |cos\theta$

说明直线的向量最主要的是影响方向，真正影响长度的是你向量本身。所以直线的向量的大小并不是关键因素

损失函数的推导

异类样本中心尽可能远

$max|||{\mu }_0|\cdot cos{\theta }_0-|{\mu }_1|\cdot cos{\theta }_1|{|}_2^2$

为了方便后续进行计算推导，同时不关心$w$的大小，所以可以乘以$|w|$

$$\max {\Vert |\mathbf{w}|\cdot \left|{\mathbf{\mu }}_0\right|\cdot \cos {\theta }_0-|\mathbf{w}|\cdot \left|{\mathbf{\mu }}_1\right|\cdot \cos {\theta }_1\Vert }_2^2$$

就可以将这个式子，转换为向量内积的形式

$$\max {\Vert {\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_0-{\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_1\Vert }_2^2$$

同类样本方差尽可能小

$$\min {\mathbf{w}}^{\mathrm{T}}{\mathbf{\Sigma }}_0\mathbf{w}$$

解释下为什么这种形式表示为方差
具体式子展开如下
其实这个式子是在投影维度上考虑的方差形式

$$\begin{array}{rl}{\mathbf{w}}^{\mathrm{T}}{\mathbf{\Sigma }}_0\mathbf{w}& ={\mathbf{w}}^{\mathrm{T}}\left(\sum _{\mathbf{x}\in X_0}\left(\mathbf{x}-{\mathbf{\mu }}_0\right){\left(\mathbf{x}-{\mathbf{\mu }}_0\right)}^{\mathrm{T}}\right)\mathbf{w}\\ & =\sum _{\mathbf{x}\in X_0}\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}-{\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_0\right)\left({\mathbf{x}}^{\mathrm{T}}\mathbf{w}-{\mathbf{\mu }}_0^{\mathrm{T}}\mathbf{w}\right)\end{array}$$

其中${\mathbf{w}}^{\mathrm{T}}\mathbf{x}-{\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_0$代表的就是投影长度之间的
${\left(w^{\top }x-w^{\top }{\mu }_0\right)}^2$形式就是类似于$(x-\bar{x}{)}^2$方差的形式

二范数

$$\Vert x{\Vert }_2={\left({\left|x_1\right|}^2+{\left|x_2\right|}^2+\cdots +{\left|x_n\right|}^2\right)}^{1/2}$$

拉格朗日乘子法

$$\begin{array}{cl}{\min }_{\mathbf{x}}& f(\mathbf{x})\\ \text{ s.t. }& h_i(\mathbf{x})=0i=1,2,\dots ,n\end{array}$$

其中自变量 $\mathbf{x}\in {\mathbb{R}}^n,f(\mathbf{x})和h_i(\mathbf{x})$ 均有连续的一阶偏导数。首先列出其拉格朗日函 数：

$L(\mathbf{x},\mathbf{\lambda })=f(\mathbf{x})+{\sum }_{i=1}^n{\lambda }_i{h}_i(\mathbf{x})$

其中 $\mathbf{\lambda }={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\right)}^{\mathrm{T}}$ 为拉格朗日乘子。然后对拉格朗日函数关于 $\mathbf{x}$ 求偏导, 并令导数等于 $0$ 再搭配约束条件 $h_i(\mathbf{x})=0$ 解出 $\mathbf{x}$ , 求解出的所有 $\mathbf{x}$ 即为上述优化问题的所有 可能【极值点】

极值点中存在最大值和最小值

最终损失函数的式子

$$\begin{array}{rl}\max J& =\frac{{\Vert {\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_0-{\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_1\Vert }_2^2}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{\Sigma }}_0\mathbf{w}+{\mathbf{w}}^{\mathrm{T}}{\mathbf{\Sigma }}_1\mathbf{w}}\\ & =\frac{{\Vert {\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_0-{\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\Vert }_2^2}{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\right)\mathbf{w}}\\ & =\frac{{\Vert {\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}\Vert }_2^2}{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\right)\mathbf{w}}\\ & =\frac{{\left[{\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}\right]}^{\mathrm{T}}{\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\right)\mathbf{w}}\\ & =\frac{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right){\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\right)\mathbf{w}}\end{array}$$

为了方便记录和讨论

设定$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$,$S_w=({\sum }_0+{\sum }_1)$

式子表示为

$$\max J=\frac{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}}$$

下一步进行求解时，由于$w$的长度完全不影响结果，所以可以先将$w$固定，添加约束${\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}=1$

通常优化问题中都考虑最小化问题，所以将式子转换为

$$\begin{array}{cl}{\min }_{\mathbf{w}}& -{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}\\ \text{ s.t. }& {\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}=1\end{array}$$

求解$w$

$$\begin{array}{cl}{\min }_{\mathbf{w}}& -{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}\\ \text{ s.t. }& {\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}=1\iff {\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}-1=0\end{array}$$

由拉格朗日乘子法可得拉格朗日函数为

$$L(\mathbf{w},\lambda )=-{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}+\lambda \left({\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}-1\right)$$

利用矩阵微分公式，对 $\mathbf{w}$ 求偏导可得

$$\begin{array}{rl}\frac{\partial L(\mathbf{w},\lambda )}{\partial \mathbf{w}}& =-\frac{\partial \left({\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}\right)}{\partial \mathbf{w}}+\lambda \frac{\partial \left({\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}-1\right)}{\partial \mathbf{w}}\\ & =-\left({\mathbf{S}}_b+{\mathbf{S}}_b^{\mathrm{T}}\right)\mathbf{w}+\lambda \left({\mathbf{S}}_w+{\mathbf{S}}_w^{\mathrm{T}}\right)\mathbf{w}\end{array}$$

由于$S_b$和$S_w$都对称 ${\mathbf{S}}_b={\mathbf{S}}_b^{\mathrm{T}},{\mathbf{S}}_w={\mathbf{S}}_w^{\mathrm{T}}$ , 所以

$$\frac{\partial L(\mathbf{w},\lambda )}{\partial \mathbf{w}}=-2{\mathbf{S}}_b\mathbf{w}+2\lambda {\mathbf{S}}_w\mathbf{w}$$

令上面的式子为0，即可得到

$${\mathbf{S}}_b\mathbf{w}=\lambda {\mathbf{S}}_w\mathbf{w}$$

将$S_b$展开后，可以得到

$$\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right){\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}=\lambda {\mathbf{S}}_w\mathbf{w}$$

${\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}$为行向量和列向量相乘，所以可以令${\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}=\gamma$

将式子进行整理，得到

$$\mathbf{w}=\frac{\gamma }{\lambda }{\mathbf{S}}_w^{-1}\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)$$

正常在利用拉格朗日乘子法进行求解的时候需要考虑约束条件，由于不关系$w$的大小，会关心方向，所以隐含的没有考虑，同时$\gamma$只受$w$影响，$\lambda$未知但是固定，所以令$\frac{\gamma }{\lambda }=1$

论证为什么使用拉格朗日乘子法求出的极值点$w$一定是最小值点

${\mu }_0$和${\mu }_1$投影后一定存在最大值和最小值

同时$-{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}=-{\Vert {\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_0-{\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_1\Vert }_2^2⩽0$

所以当求出的极值点代入到目标函数的式子中，不为0的点就是最小值点

拓展到多线性判别分析

$$W=(w_1,w_2,...,w_n)$$

$$S_b(w_1,w_2,...,w_3)=\lambda S_w(w_1,w_2,...,w_3)$$

$$S_b{w}_1=\lambda S_w{w}_1$$

相当于是$n$个二分类的线性判别问题

补充数学知识

广义特征值

$Ax=\lambda x$，普通求特征值

$Ax=\lambda Bx$, 广义特征值

其中$A$和$B$为$n$阶方阵，称$\lambda$为$A$相对于$B$的广义特征值

$x$为$A$相对于$B$的属于广义特征值$\lambda$的特征向量

广义瑞利商

设 $\mathbf{A},\mathbf{B}$ 为$n$阶厄米 (Hermitian) 矩阵, 且 $\mathbf{B}$ 正定, 称 $R(\mathbf{x})=\frac{{\mathbf{x}}^{\mathrm{H}}\mathbf{A}\mathbf{x}}{{\mathbf{x}}^{\mathrm{H}}\mathbf{B}\mathbf{x}}(\mathbf{x}\ne 0)$ 为 $\mathbf{A}$ 相对于 $\mathbf{B}$ 的广义瑞利商。特别地, 当 $\mathbf{B}=\mathbf{I}$ (单位矩阵) 时, 广义瑞利商退化为瑞利商。

(这里可以先简单理解为厄米矩阵是对称矩阵)

广义瑞利商的性质：设 ${\lambda }_i,{\mathbf{x}}_i(i=1,2,\dots ,n)$ 为 $\mathbf{A}$ 相对于 $\mathbf{B}$ 的广义特征值和特征向量, 且 $lambda_{1} leqslant lambda_{2} leqslant ldots leqslant lambda_{n} $。

$$\begin{array}{l}{\min }_{\mathbf{x}\ne 0}R(\mathbf{x})=\frac{{\mathbf{x}}^{\mathrm{H}}\mathbf{A}\mathbf{x}}{{\mathbf{x}}^{\mathrm{H}}\mathbf{B}\mathbf{x}}={\lambda }_1,{\mathbf{x}}^{\ast }={\mathbf{x}}_1\\ {\max }_{\mathbf{x}\ne 0}R(\mathbf{x})=\frac{{\mathbf{x}}^{\mathrm{H}}\mathbf{A}\mathbf{x}}{{\mathbf{x}}^{\mathrm{H}}\mathbf{B}\mathbf{x}}={\lambda }_n,{\mathbf{x}}^{\ast }={\mathbf{x}}_n\end{array}$$

【证明】：当固定 ${\mathbf{x}}^{\mathrm{H}}\mathbf{B}\mathbf{x}=1$ 时，使用拉格朗日乘子法可推得 $\mathbf{A}\mathbf{x}=\lambda \mathbf{B}\mathbf{x}$ 这样一个广义特征值问题, 因此 $\mathbf{x}$ 所有可能的解即为 ${\mathbf{x}}_i(i=1,2,\dots ,n)$ 这 $\mathrm{n}$ 个广义特征向量, 将其分别代入 $R(\mathbf{x})$ 即可推得上述结论。

其实也就是将特征值由小到大排列，然后需要几个解，就按照顺序取几个特征值对应的特征向量

参考资料

[1]周志华. 《机器学习》[J]. 中国民商, 2016, 03(No.21):93-93.
[2]机器学习公式详解

最后

以上就是丰富早晨为你收集整理的【机器学习-西瓜书】-第3章-线性回归-学习笔记-下3.3 对数几率回归3.4 线性判别分析参考资料的全部内容，希望文章能够帮你解决【机器学习-西瓜书】-第3章-线性回归-学习笔记-下3.3 对数几率回归3.4 线性判别分析参考资料所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。