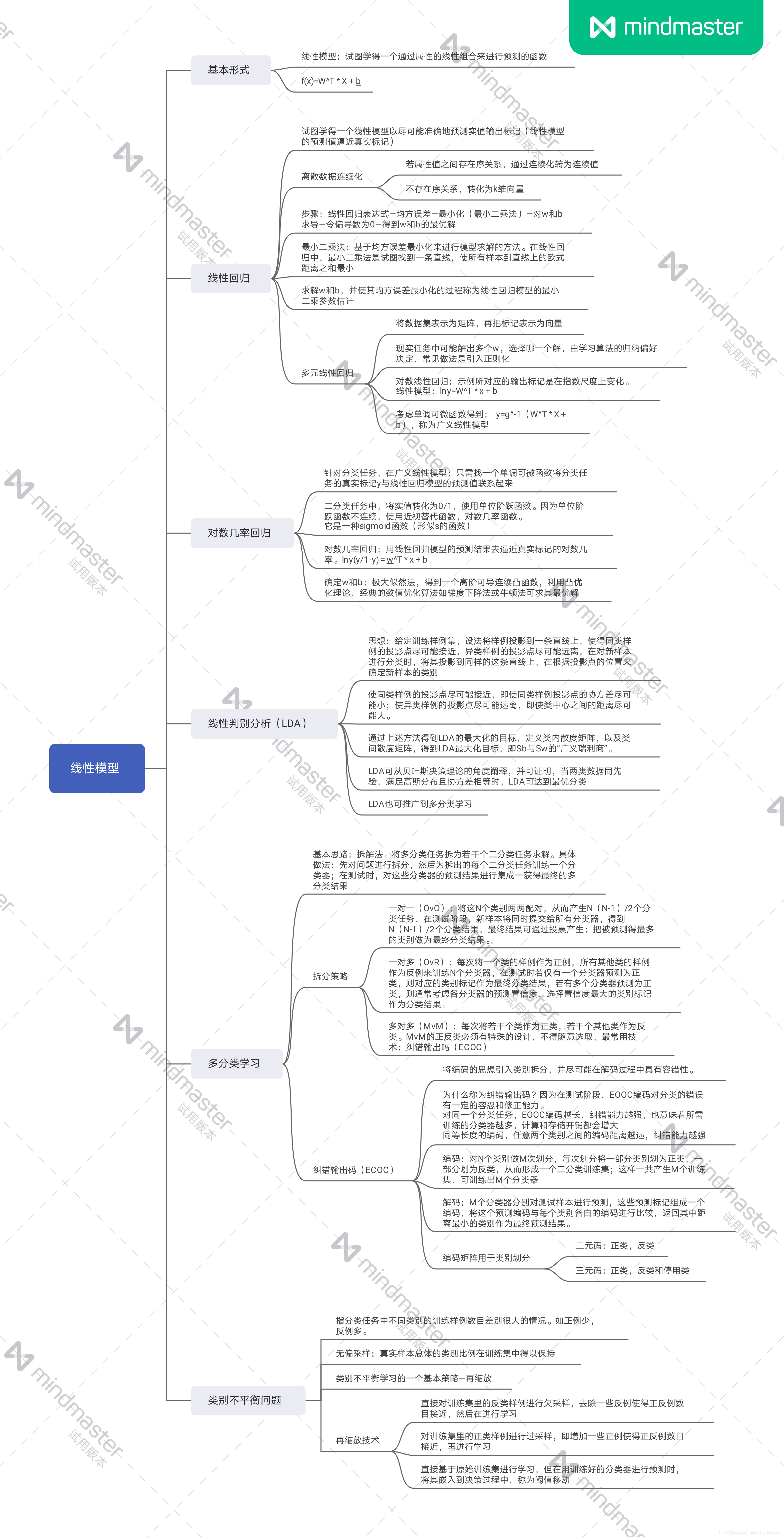
3.1基本形式

给定由 d 个属性描述的示例 x = (x1;x2;…;xd) ，其中 xi 是 x 在第 i 个属性上的取值，线性模型（linear model）试图学得一个通过属性的线性组合来进行预测的函数，即

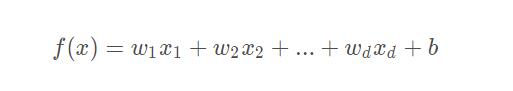
一般用向量形式写成

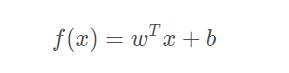
非线性模型（nonlinear model）可在线性模型的基础上通过引入层级结构或高维映射而得。此外，由于 w 直观表达了个属性在预测中的重要性，因此线性模型有很好的可解释性（comprehensibility）。

3.2线性回归

给定数据集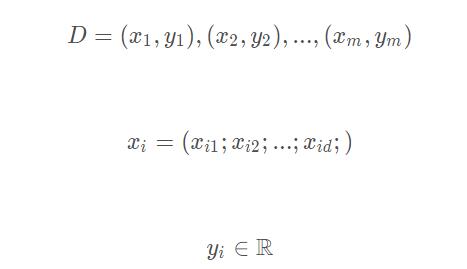
线性回归试图学得一个线性模型来尽可能的准确预测实值输出标记。

对离散属性，若属性之间存在“序”（order）的关系，可通过连续化将其转化为连续值。例如“高”和“矮”可以转化为{1.0，0.0}，“高”、“中”、“低“可以转化为{1.0，0.5，0.0}。若属性之间不错在序关系，假定有 k 个属性值，则通常转化为 k 维向量。例如”西瓜“、”黄瓜“、”南瓜“可以转化为(0,0,1),(0,1,0),(1,0,0)。
线性回归试图学得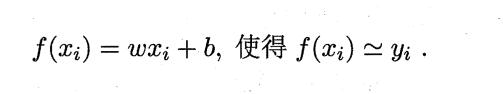
均方误差最小化：可以求得 w 和 b，对应了”欧氏距离“，基于均方误差最小化来进行求解的方法称为”最小二乘法“——试图找到一条直线，使得所有样本到直线的欧氏距离之和最小。

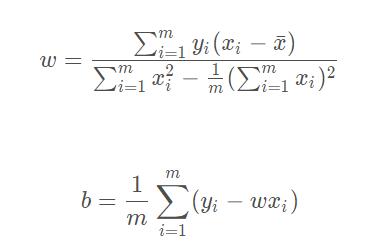
其中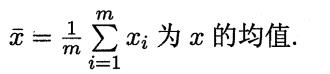
对数线性回归：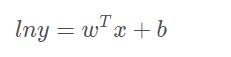
广义线性模型：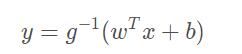
其中g为单调可微函数，称为“联系函数”。

3.3对数几率回归

对于二分类任务，最理想的是”单位阶跃函数“，但是其不连续，不能直接用于上文中的 g-(.)，所以一般使用对数几率函数：

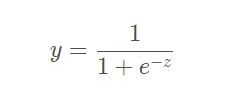
将其作为 g-(.) 代入得：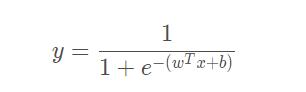
即：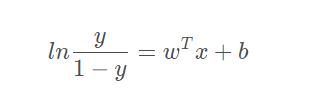
其对应的模型称为”对数几率回归“（logistic regression），是一种分类学习方法。这种方法有很多优点：

1. 直接对分类可能性进行建模，无需事先假设数据分布，避免了假设分布不准确带来的问题;
2. 不是仅预测出类别，而是可得到近似概率预测，这对许多需要利用概率辅助决策的任务很有用;
3. 对率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都课直接用于求取最优解

3.4线性判别分析（Linear Discriminant Analysis ，简称LDA）

亦称 Fisher判别分析。
LDA 的思想：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能近、异类样例的投影点尽可能远；对新样本进行分类时，将其投影到这条线上，再根据投影点的位置来确定类别。

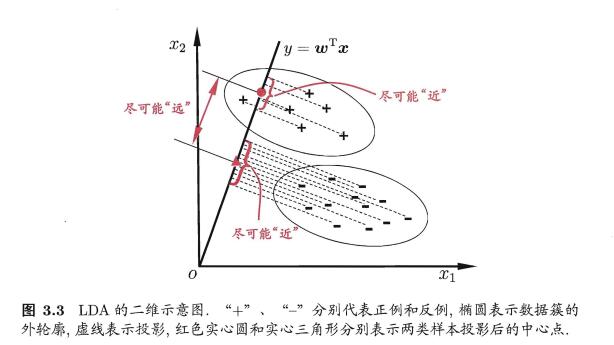
类内散度矩阵(within-class scatter matrix)：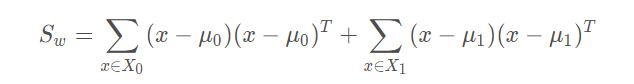
类间散度矩阵(between class scatter matrix)：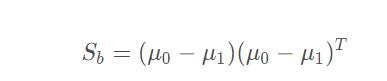
欲最大化的目标：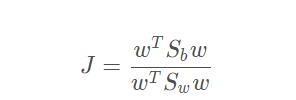
即 Sb 与 Sw 的”广义瑞利商“(generalized Rayleigh quotiet)。

3.5多分类学习

基本思路：”拆解法“，将多分类任务拆解为若干个二分类任务求解。涉及到多分类任务的拆分，以及对多个分类器的集成。

经典拆分策略：

1.一对一（OvO）One
将 N 个类别两两配对，从而产生 N(N-1)/2 个分类任务，最终结果可通过投票产生，把被预测的最多的作为分类结果。
2.一对其余（OvR）Rest
每次将一个类作为正例，其他所有类作为反例来训练 N 个分类器。在测试时，若只有一个分类器预测为正类，则作为最终分类结果。若有多个分类器预测为正类，则通常考虑各分类器的预测置信度，选择置信度最大的类别标记作为分类结果。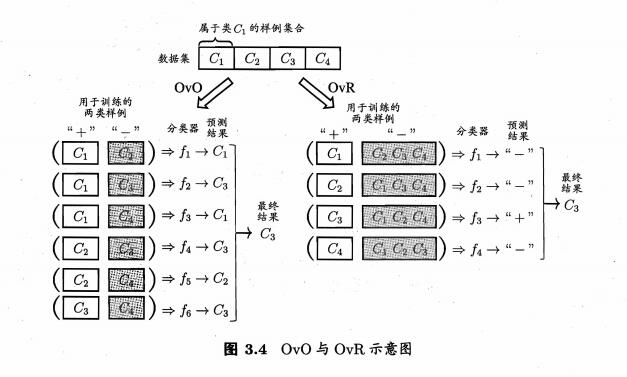
3.多对多（MvM）Many
每次将若干个类作为正类，若干个其他类作为反类。正反类的构造必须有特殊的设计，通常使用”纠错输出码“(Error Correcting Output Codes，简称 ECOC)。
纠错输出码（ECOC），将编码的思想引入类别拆分，并尽可能在解码过程中具有容错性。其工作过程分为两步：

1. 编码：对 N 个类别做 M 次划分，形成 M 个二分类训练集，训练出 M 个分类器。
2. 解码：M 个分类器分别对测试样本进行预测，这些预测标记组成一个编码，将这个预测编码与每个类各自的编码进行比较，返回其中距离最小的类别作为最终预测结果。

类别划分通过“编码矩阵”(coding matrix) 指定，常见的有二元码和三元码。前者将每个类别分别指定为正类和反类；后者在正反类之外，还可以指定“停用类”。

一般来说，对同一个学习任务， ECOC 编码越长，纠错能力越强.
对同等长度的编码，理论上来说，任意两个类别之间的编码距离越远，则纠错能力越强.

3.6类别不平衡问题

类别不平衡(class-imbalance) ，指分类任务中不同类别的训练样例数目差别很大的情况。

“再缩放”策略：只要分类器的预测几率，高于观测几率，就应判断为正例，即

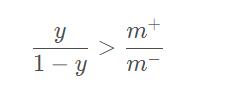
则预测为正例。

常用三种做法：

1. 欠采样：去除一些反例，使得正反例数目接近。
2. 过采样：增加一些正例，使得正反例数目接近。
3. 阈值移动：上文“再缩放”策略。
   
   参考博文链接https://blog.csdn.net/qq_38962336/article/details/106397677

最后

以上就是伶俐小虾米为你收集整理的西瓜书学习笔记第3章（线性模型）3.1基本形式3.2线性回归3.3对数几率回归3.4线性判别分析（Linear Discriminant Analysis ，简称LDA）3.5多分类学习3.6类别不平衡问题的全部内容，希望文章能够帮你解决西瓜书学习笔记第3章（线性模型）3.1基本形式3.2线性回归3.3对数几率回归3.4线性判别分析（Linear Discriminant Analysis ，简称LDA）3.5多分类学习3.6类别不平衡问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。