目录

12-5 CART与决策树中的超参数

复杂度

决策树解决回归问题

决策树的局限性

12-5 CART与决策树中的超参数

是一棵二叉树

复杂度

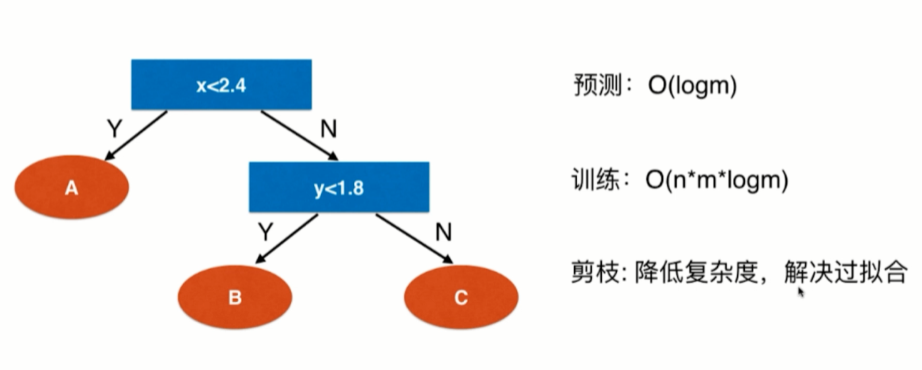
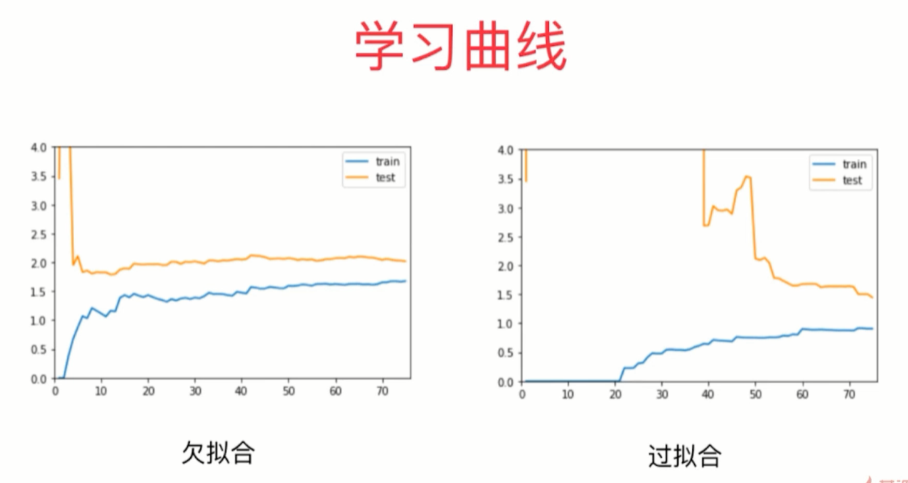
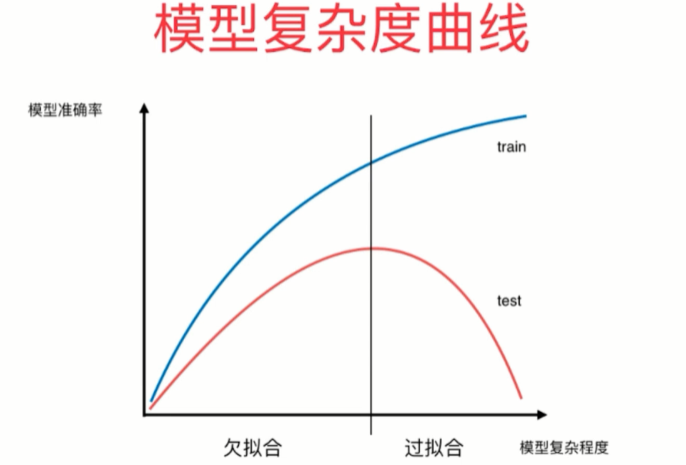
非参数学习容易过拟合

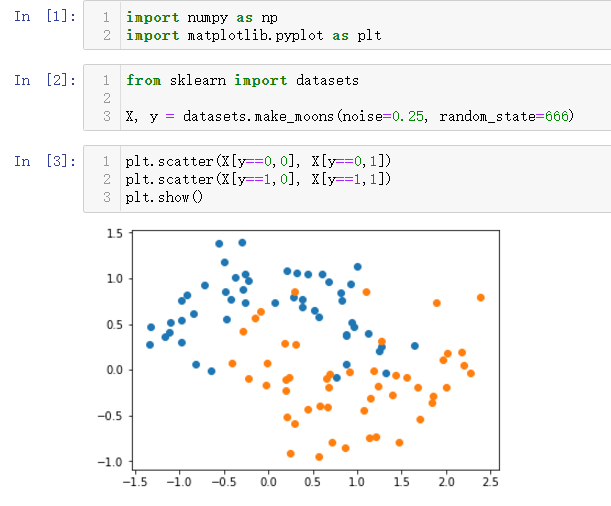
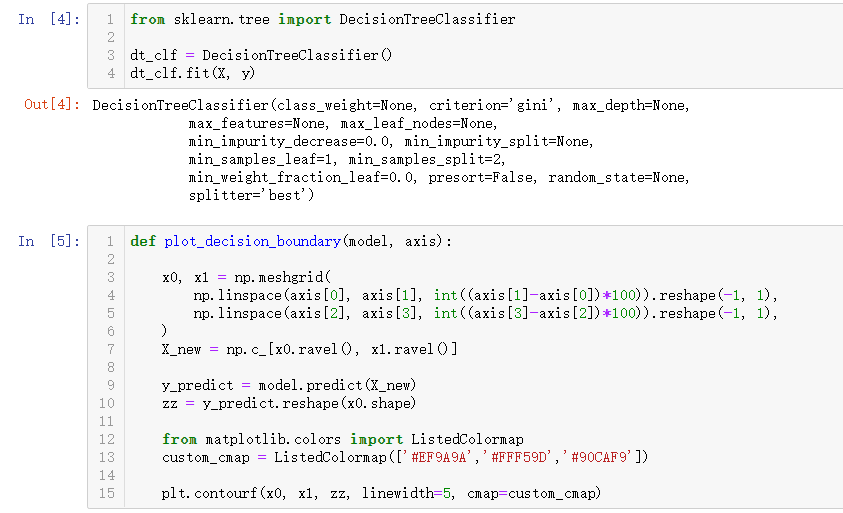
from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier()
dt_clf.fit(X, y)

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

默认决策树gin系数，没有深度限制

非常不规则过拟合，修改参数防止过拟合

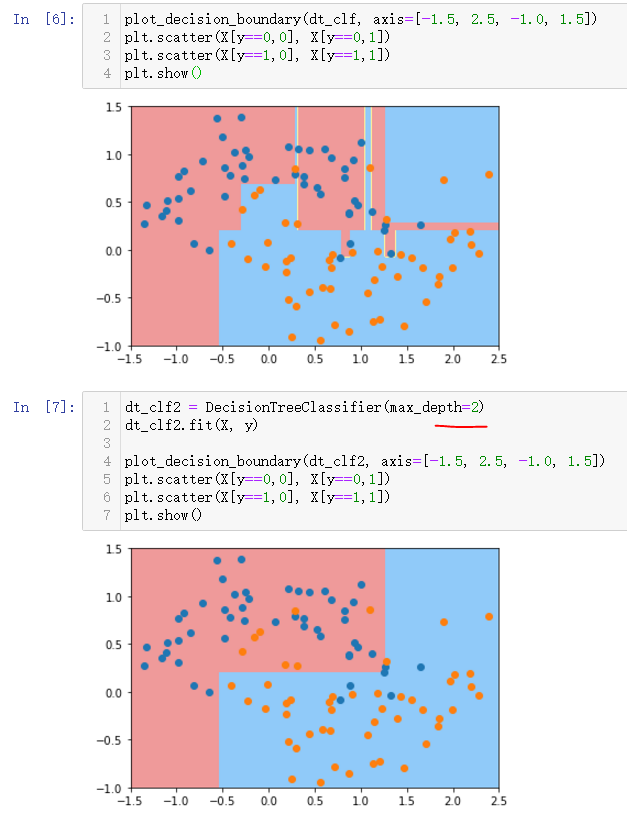
深度

dt_clf2 = DecisionTreeClassifier(max_depth=2)
dt_clf2.fit(X, y)

plot_decision_boundary(dt_clf2, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

至少有10个样本才划分

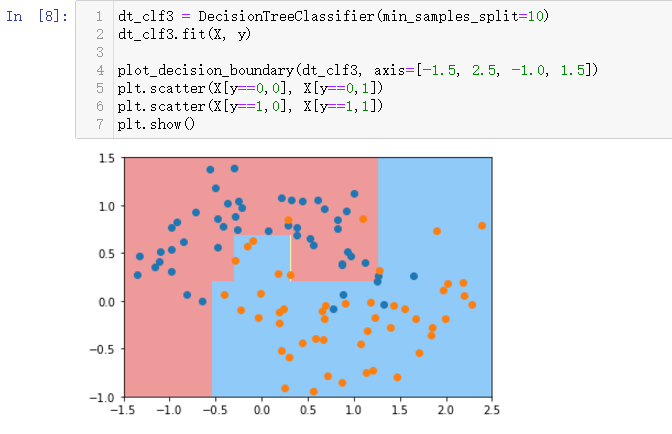
min-samples-leaf叶子节点为6个样本

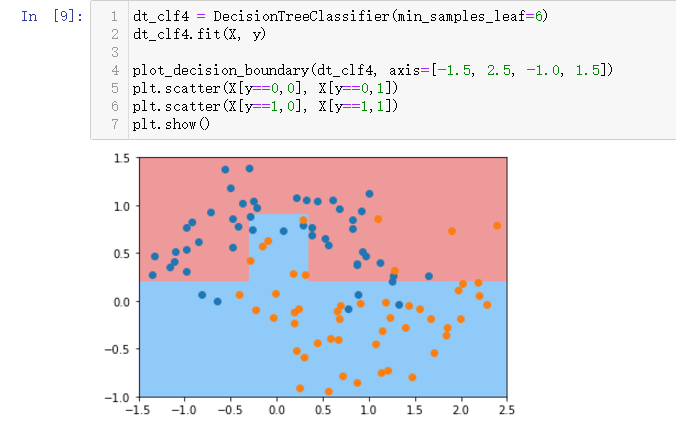
max-leaf-modes最多有多少个叶子节点

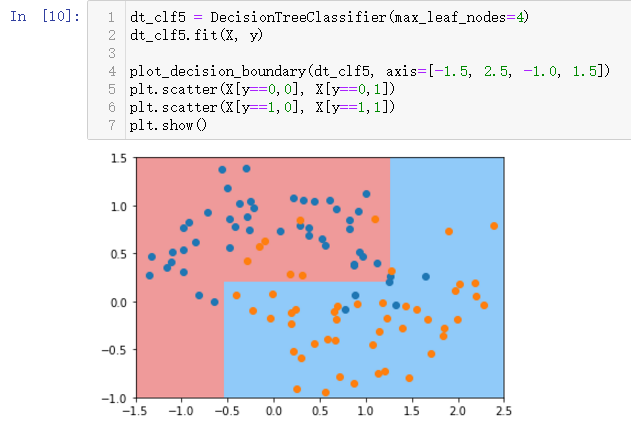
可以相互组合，通过网格搜索，其它的参数学习官方文档

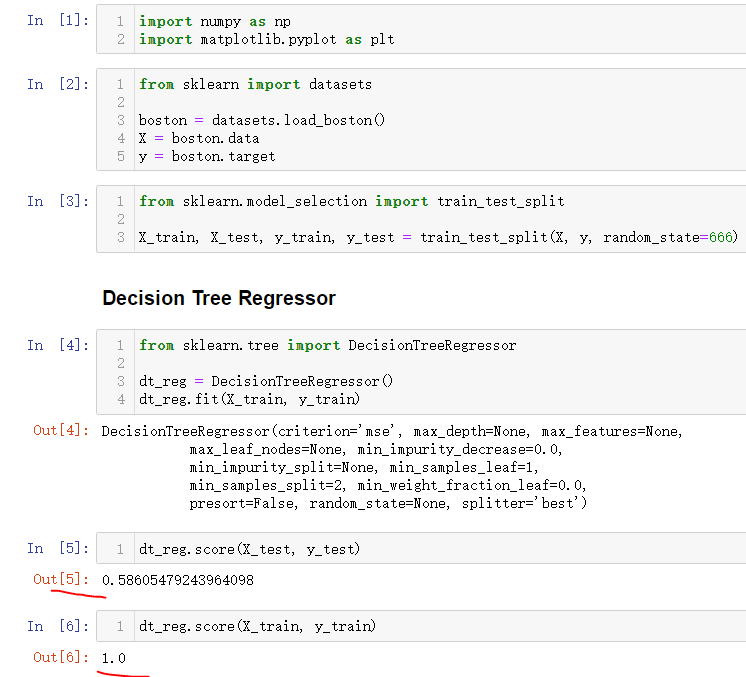
决策树解决回归问题

叶子节点是类别则投票，如果是具体的一个数则就是回归问题要解决的问题

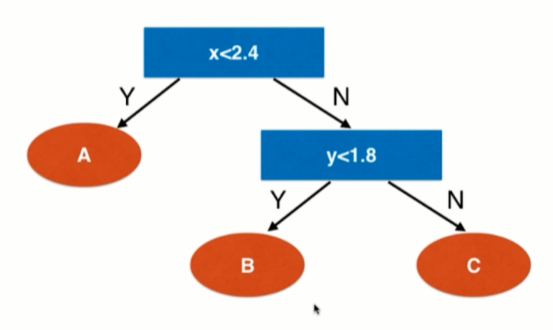
决策树的局限性

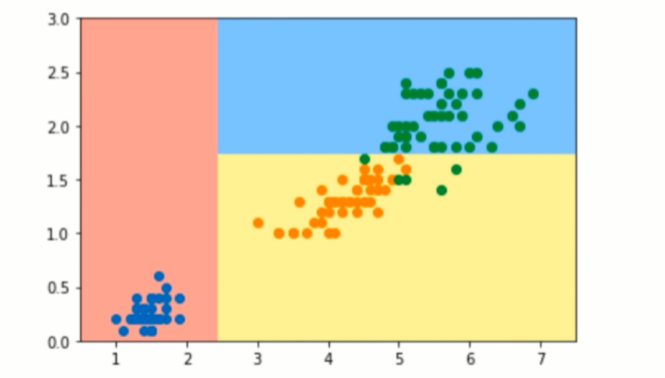
边界是横平竖直的

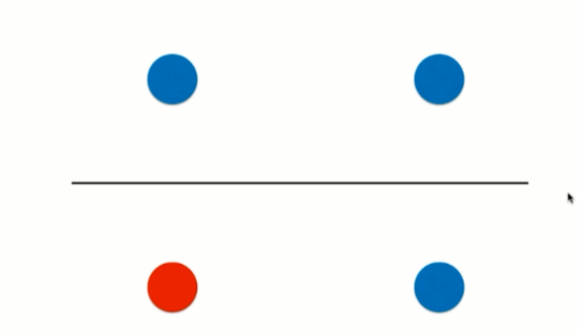
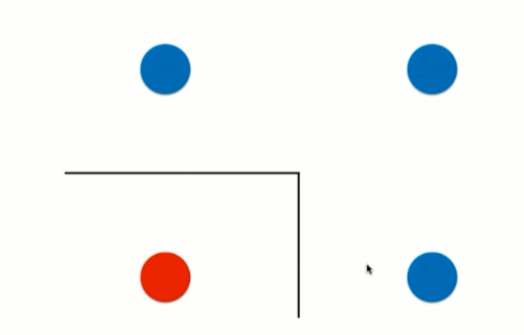
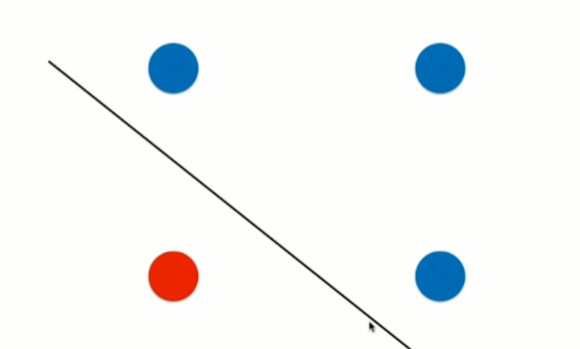
决策树不可能产生这样的生斜线

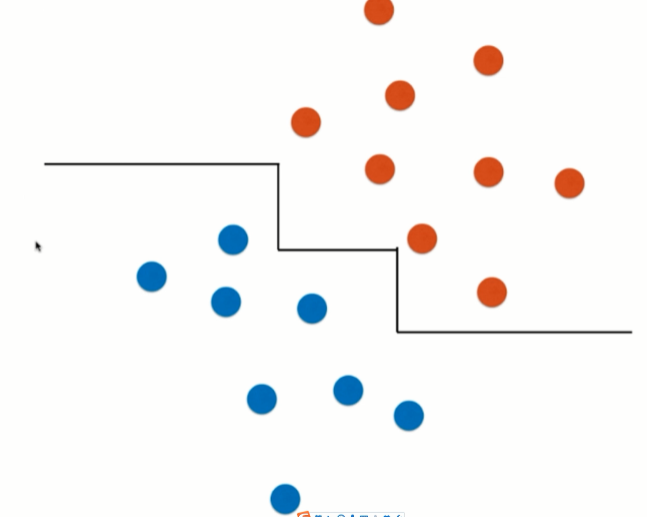
两端可能错的离谱

对个别数据敏感

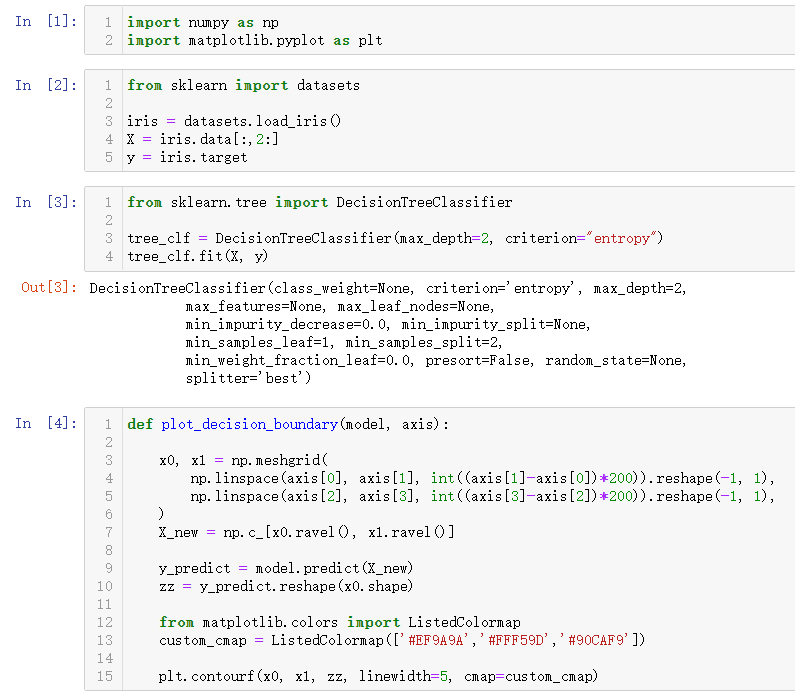
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data[:,2:]
y = iris.target


from sklearn.tree import DecisionTreeClassifier

tree_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy")
tree_clf.fit(X, y)

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*200)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*200)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)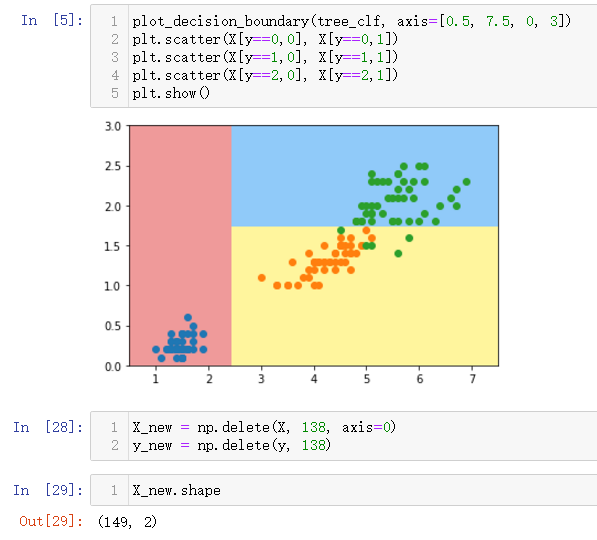

plot_decision_boundary(tree_clf, axis=[0.5, 7.5, 0, 3])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.show()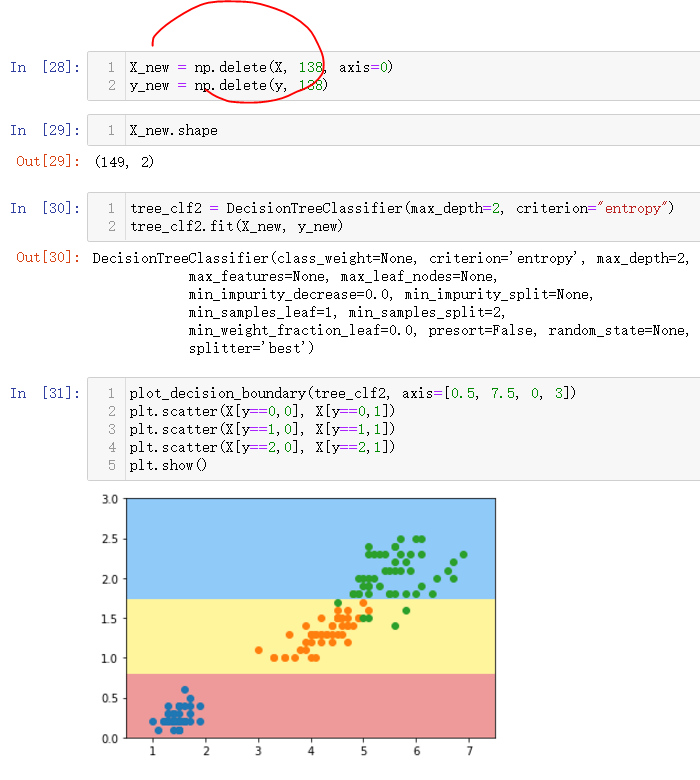

只删除了一个参数，就变化这么大

最后

以上就是柔弱镜子最近收集整理的关于第12章 决策树 学习笔记中12-5 CART与决策树中的超参数决策树解决回归问题决策树的局限性的全部内容，更多相关第12章内容请搜索靠谱客的其他文章。