???? 『精品学习专栏导航帖』

• ????最适合入门的100个深度学习实战项目????
• ????【PyTorch深度学习项目实战100例目录】项目详解 + 数据集 + 完整源码????
• ????【机器学习入门项目10例目录】项目详解 + 数据集 + 完整源码????
• ????【机器学习项目实战10例目录】项目详解 + 数据集 + 完整源码????
• ????Java经典编程100例????
• ????Python经典编程100例????
• ????蓝桥杯历届真题题目+解析+代码+答案????
• ????【2023王道数据结构目录】课后算法设计题C、C++代码实现完整版大全????

2021人工智能领域新星创作者，带你从入门到精通，该博客每天更新，逐渐完善机器学习各个知识体系的文章，帮助大家更高效学习。

一、概述

首先在讲高斯判别分析之前先看一下线性分类的几种常见模型。

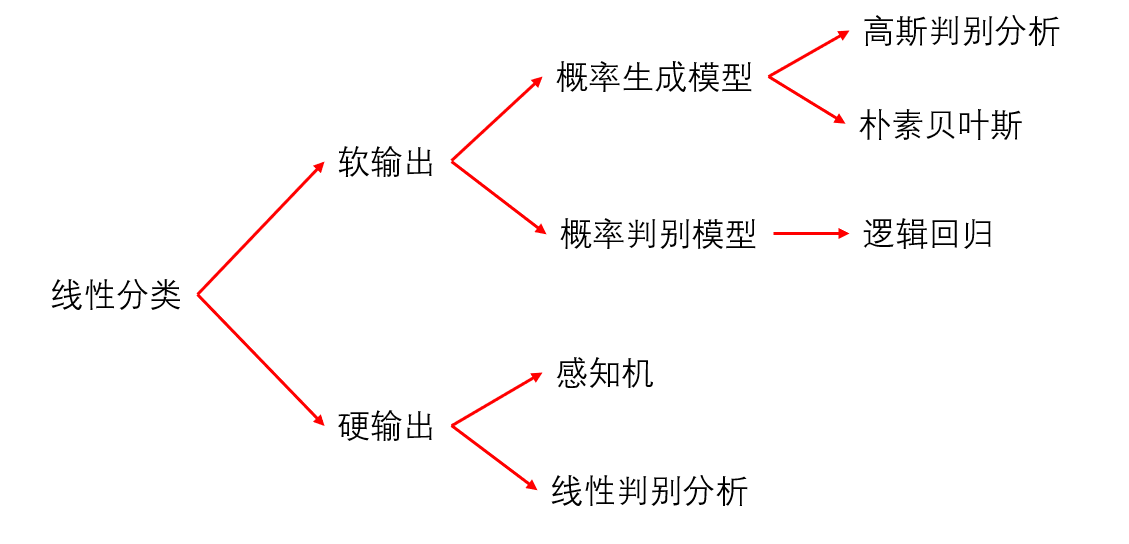
• 软输出：就是通过概率的方式进行构建模型

• 硬输出：非概率方式

• 概率判别模型：判别模型就是会直接求 $P(Y|X)$ 的值用于不同类别概率的比较

• 概率生成模型：它是通过贝叶斯方式将 $P(Y|X)$进行展开然后进而计算

本片文章将重点讲述概率生成模型——高斯判别分析

二、高斯判别分析

1.算法思想

首先我们得高斯判别分析属于一种概率生成模型，所以它是会使用概率的方式进行建模 $P(Y|X)$ ，这个概率为后验概率，它的意思就是在样本X的前提下，Y属于不同类别的概率，我们会比较不同类别的概率，概率大的Y作为最终的分类类别。

那么显然这里我们可以使用MLE进行估计：
$$\begin{gathered} MLE:L(\theta )=logP(Y|X) \\ =log\frac{P(Y)P(X|Y)}{P(X)} \end{gathered}$$
采用对数似然估计的方式来估计参数，这里的 X和Y都会服从一种分布，我们可以将他们的概率密度公式进行带入，又因为分母 $P(X)$对于整个表达式来说是一个常数，所以我们的研究重点是分子，我们的目标就是：
$$argma{x}_{\theta }log[P(Y)P(X|Y)]$$

2.数据的分布假设

由于我们是基于二分类进行建模，所以y的取值只有0或者1，所以我们可以假设我们的标签y服从伯努利分布，即：
$$y\sim Bernoulli(\varphi )$$

$$P(y)={\varphi }^y(1-\varphi {)}^{1-y}$$

如果当y=1时，$P(y)$ 的值为 $\varphi$​ ，就是y发生的概率，如果y=0，此时 $P(y)$ 的值为 $1-\varphi$ 就是y不发生的概率。

针对于数据X，我们也是假设其符合分布，我们用一幅图表示一下：

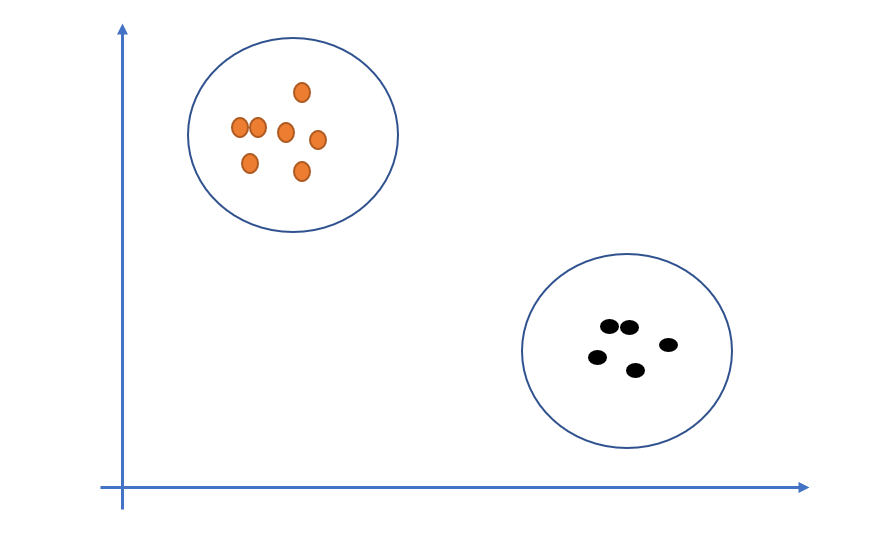
由于两类样本是分布在不同的区域内的，相同的样本都是在同一区域，所以我们可以假设两个类别的数据分别服从高斯分布，为什么使用高斯分布？是因为高斯分布的数学性质好，而且更容易模拟真实生活中的样本分布。

所以数据X的分布：
$$\begin{gathered} x|(y=1)\sim N({\mu }_1,\Sigma ) \\ x|(y=0)\sim N({\mu }_2,\Sigma ) \end{gathered}$$
所以数据X的概率密度函数为：
$$P(x|y)=N({\mu }_1,\Sigma {)}^{y}N({\mu }_2,\Sigma {)}^{1-y}$$

3.最大似然估计

我们希望 $P(Y|X)$ 的概率越大越好，也就是说在数据X的前提下，我们根据样本X的建模获得的Y对的几率越大越好，所以我们的目标函数就为：
$$\begin{gathered} argma{x}_{\theta }logP(Y|X) \\ =argmaxlog\frac{P(Y)P(X|Y)}{P(X)} \end{gathered}$$
此时的分母作为常数我们不需要管，我们只注重分子的大小，而分子恰恰就是我们上面定义的概率密度函数，有时也称 $P(Y)$ 叫先验概率，$P(X|Y)$ 是似然。

所以我们的目标函数可以转化为：
$$\begin{gathered} argmaxlog\frac{P(Y)P(X|Y)}{P(X)} \\ =argmaxlog[P(y)P(x|y)] \\ =argmax\sum _{i=1}^m[logp(y_i)+logp(x_i|y_i)] \\ =argmax\sum _{i=1}^{m}log{\varphi }_i^y(1-\varphi {)}^{1-y_i}+logN({\mu }_1,\Sigma {)}^{y_i}+logN({\mu }_2,\Sigma {)}^{1-y_i} \end{gathered}$$
该式子中的参数分别为 $\varphi 、{\mu }_1、{\mu }_2、\Sigma$ ，所以我们要对上式求导，分别求取使目标函数达到极值的极值点。

4. 求解参数 $\varphi$

最终的目标函数中只有第一项是与 $\varphi$ 有关的，所以只需要考虑这一项即可。

该式可以写为：
$$\sum _{i=1}^m{y}_i(log\varphi )+(1-y_i)log(1-\varphi )$$
对该式进行求导可以获得：
$$\frac{\partial L}{\partial \varphi }=\sum _{i=1}^m\frac{y_i}{\varphi }-\frac{1-y_i}{1-\varphi }=0$$
进而可得：
$$\sum _{i=1}^m{y}_i(1-\varphi )-(1-y_i)\varphi =0$$

$$\sum _{i=1}^m(y_i-\varphi )=0$$

所以可以解得：
$$\varphi =\frac{1}{m}\sum _{i=1}^m{y}_1$$
这里我们约定一下，总样本数为 $N$ ，其中类别为1的有 $N_1$ 个，类别为0的有 $N_2$ 个，上面的推导写成m是我的书写习惯了，用m代表总样本数，接下来的总样本数为N。

所以我们最终的 $\varphi$ 就为：
$$\varphi =\frac{N_1}{N}$$
因为后面是对 $y_i$ 进行求和，而 $y_i$ 只有0和1分类，只有当y=1时才有效，而y=1类别有 $N_1$ 个样本，所以可以改写为上面的式子。

5.求解参数 ${\mu }_1$

目标函数：
$$argmax\sum _{i=1}^{m}log{\varphi }_i^y(1-\varphi {)}^{1-y_i}+logN({\mu }_1,\Sigma {)}^{y_i}+logN({\mu }_2,\Sigma {)}^{1-y_i}$$
参数 ${\mu }_1$ 只和第二项有关，所以接下来处理求导只针对于它。

因为我们之间假设了X服从高斯分布，所以概率密度公式为：
$$\begin{gathered} N({\mu }_1,\Sigma )=p(x|y) \\ =\frac{1}{(2\pi {)}^{\frac{p}{2}}|\Sigma {|}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-y)) \end{gathered}$$
我们现在对目标函数的第二项进行化简处理：
$$\begin{gathered} \sum _{i=1}^{m}logN({\mu }_1,\Sigma {)}^{y_i} \\ =\sum _{i=1}^m{y}_{i}logN({\mu }_i,\Sigma ) \\ =\sum _{i=1}^m{y}_{i}log\frac{1}{(2\pi {)}^{\frac{p}{2}}|\Sigma {|}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-y)) \end{gathered}$$
所以我们可以转化为：
$$\sum _{i=1}^m{y}_i[-\frac{1}{2}(x-{\mu }_1{)}^T{\Sigma }^{-1}(x-{\mu }_1)]$$
为什么化成了该式，因为上面的式子利用 log性质拆开后，都是常数，与参数 ${\mu }_1$ 无关，所以就省略了。

之后我们对该式进行求导：
$$\frac{\partial L}{\partial {\mu }_1}=\sum _{i=1}^m{y}_i(-\frac{1}{2})[{\Sigma }^{-1}(x-{\mu }_1)d(x-{\mu }_1{)}^T+(x-{\mu }_1{)}^T{\Sigma }^{-1}d(x-{\mu }_1)]=0$$

$$\sum _{i=1}^{m}2{\Sigma }^{-1}({\mu }_1-x)y_i(-\frac{1}{2})=0$$

$$\sum _{i=1}^m{y}_i{\Sigma }^{-1}{x}_i=\sum _{i=1}^m{y}_i{\Sigma }^{-1}{\mu }_1$$

所以我们可以获得最终的解：
$$\begin{gathered} {\mu }_1=\frac{{\sum }_{i=1}^m{y}_i{x}_i}{{\sum }_{i=1}^m{y}_1} \\ =\frac{{\sum }_{i=1}^m{y}_i{x}_i}{N_1} \end{gathered}$$

6.求解参数 ${\mu }_2$

由于参数 ${\mu }_2$ 和 ${\mu }_1$ 的求解方式类似，这里就省略了

7.求解参数 $\Sigma$

目标函数：
$$argmax\sum _{i=1}^{m}log{\varphi }_i^y(1-\varphi {)}^{1-y_i}+logN({\mu }_1,\Sigma {)}^{y_i}+logN({\mu }_2,\Sigma {)}^{1-y_i}$$
我们可以看到 $\Sigma$ 与函数中的后两项都存在关系。

所以可以获得：
$$\begin{gathered} argmax\sum _{i=1}^{m}logN({\mu }_1,\Sigma {)}^{y_i}+logN({\mu }_2,\Sigma {)}^{1-y_i} \\ =\sum _{i=1}^m{y}_{i}logN({\mu }_1,\Sigma )+(1-y_i)logN({\mu }_2,\Sigma ) \\ =\sum _{x_i\in C_1}logN({\mu }_1,\Sigma )+\sum _{x_i\in C_2}logN({\mu }_2,\Sigma ) \end{gathered}$$
其中第三部我们将其化简，为了表示方便，我们拆分成两个类别的求和，分别属于两个类的样本，这样就可以把 $y$ 值去掉。

发现最终的结果，是两个通项公式的求和，所以我们接下来求一下这个通项公式 $\sum logN(\mu ,\Sigma )$ ：
$$\begin{gathered} \sum _{i=1}^{m}logN(\mu ,\Sigma )=\sum _{i=1}^{m}log\frac{1}{(2\pi {)}^{\frac{p}{2}}|\Sigma {|}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-y)) \\ =\sum _{i=1}^{m}log\frac{1}{(2\pi {)}^{\frac{p}{2}}}+log|\Sigma {|}^{-\frac{1}{2}}-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ) \\ =C-\frac{N}{2}log|\Sigma |-\frac{1}{2}\sum _{i=1}^{m}tr((x-\mu {)}^T{\Sigma }^{-1}(x-\mu )) \\ =C-\frac{N}{2}log|\Sigma |-\frac{1}{2}tr(\sum _{i=1}^m(x-\mu )(x-\mu {)}^T{\Sigma }^{-1}) \\ =C-\frac{N}{2}log|\Sigma |-\frac{1}{2}Ntr(S{\Sigma }^{-1}) \end{gathered}$$
所以将我们目标函数分别带入通项公式中的结果：
$$\begin{gathered} \sum _{x_i\in C_1}logN({\mu }_1,\Sigma )+\sum _{x_i\in C_2}logN({\mu }_2,\Sigma ) \\ =-\frac{1}{2}[Nlog|\Sigma |+N_{1}tr(S_1{\Sigma }^{-1})+N_{2}tr(S_2{\Sigma }^{-1})] \end{gathered}$$
所以我们需要对上式进行求导：
$$\frac{\partial L}{\partial \Sigma }=-\frac{1}{2}(N{\Sigma }^{-1}-N_1{S}_1{\Sigma }^{-1}-N_2{S}_2{\Sigma }^{-1})=0$$
解得参数 $\Sigma$ ：
$$\Sigma =\frac{N_1{S}_1+N_2{S}_2}{N}$$

8.特别公式

上面求导或者化简可能用到的公式：
$$tr(A)=A(A为标量)$$

$$tr(ABC)=tr(CAB)=tr(BCA)$$

$$\frac{\partial |A|}{\partial A}=|A|A^{-1}$$

$$\frac{\partial tr(AB)}{\partial A}=B^T$$

写在最后

        大家好，我是阿光，觉得文章还不错的话，记得“一键三连”哦！！！

最后

以上就是迅速花瓣最近收集整理的关于【机器学习】线性分类——高斯判别分析GDA（理论+图解+公式推导）一、概述二、高斯判别分析的全部内容，更多相关【机器学习】线性分类——高斯判别分析GDA（理论+图解+公式推导）一、概述二、高斯判别分析内容请搜索靠谱客的其他文章。