高斯模糊是一种图像模糊滤波器,它用正态分布计算图像中每个像素的变换。N 维空间正态分布方程为
在二维空间定义为
其中 r 是模糊半径 (r2 = u2 + v2),σ 是正态分布的标准偏差。在二维空间中,这个公式生成的曲面的等高线是从中心开始呈正态分布的同心圆。分布不为零的像素组成的卷积矩阵与原始图像做变换。每个像素的值都是周围相邻像素值的加权平均。原始像素的值有最大的高斯分布值,所以有最大的权重,相邻像素随着距离原始像素越来越远,其权重也越来越小。这样进行模糊处理比其它的均衡模糊滤波器更高地保留了边缘效果,参见尺度空间实现。
理论上来讲,图像中每点的分布都不为零,这也就是说每个像素的计算都需要包含整幅图像。在实际应用中,在计算高斯函数的离散近似时,在大概3σ距离之外的像素都可以看作不起作用,这些像素的计算也就可以忽略。通常,图像处理程序只需要计算 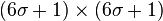 的矩阵就可以保证相关像素影响。
的矩阵就可以保证相关像素影响。
除了圆形对称之外,高斯模糊也可以在二维图像上对两个独立的一维空间分别进行计算,这叫作线性可分。这也就是说,使用二维矩阵变换得到的效果也可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到。从计算的角度来看,这是一项有用的特性,因为这样只需要 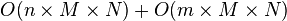 次计算,而不可分的矩阵则需要
次计算,而不可分的矩阵则需要 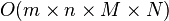 次计算,其中 M,N 是需要进行滤波的图像的维数,m、n 是滤波器的维数。
次计算,其中 M,N 是需要进行滤波的图像的维数,m、n 是滤波器的维数。
对一幅图像进行多次连续高斯模糊的效果与一次更大的高斯模糊可以产生同样的效果,大的高斯模糊的半径是所用多个高斯模糊半径平方和的平方根。例如,使用半径分别为 6 和 8 的两次高斯模糊变换得到的效果等同于一次半径为 10 的高斯模糊效果,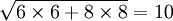 。根据这个关系,使用多个连续较小的高斯模糊处理不会比单个高斯较大处理时间要少。
。根据这个关系,使用多个连续较小的高斯模糊处理不会比单个高斯较大处理时间要少。
在减小图像尺寸的场合经常使用高斯模糊。在进行欠采样的时候,通常在采样之前对图像进行低通滤波处理。这样就可以保证在采样图像中不会出现虚假的高频信息。高斯模糊有很好的特性,如没有明显的边界,这样就不会在滤波图像中形成震荡。
/*权重函数,使用两个一维高斯函数进行卷积,之所以使用了二维的形式是因为便于统一 调用,下面的调用过程中x或y必有一个为0 */
float GetGaussianDistribution( float x, float y, float rho ) {
float g = 1.0f / sqrt( 2.0f * 3.141592654f * rho * rho );
return g * exp( -(x * x + y * y) / (2 * rho * rho) );
}
void GetGaussianOffsets( bool bHorizontal, D3DXVECTOR2 vViewportTexelSize,
D3DXVECTOR2* vSampleOffsets, float* fSampleWeights ) {
// Get the center texel offset and weight
fSampleWeights[0] = 1.0f * GetGaussianDistribution( 0, 0, 2.0f );
vSampleOffsets[0] = D3DXVECTOR2( 0.0f, 0.0f );
// Get the offsets and weights for the remaining taps
if( bHorizontal ) {
for( int i = 1; i < 15; i += 2 ) {
vSampleOffsets[i + 0] = D3DXVECTOR2( i * vViewportTexelSize.x, 0.0f ); //纹理坐标偏移,计算纹理坐标值(像素右方7像素)
vSampleOffsets[i + 1] = D3DXVECTOR2( -i * vViewportTexelSize.x, 0.0f ); //像素左方7像素
fSampleWeights[i + 0] = 2.0f * GetGaussianDistribution( float(i + 0), 0.0f, 3.0f ); //原像素左方权重值
fSampleWeights[i + 1] = 2.0f * GetGaussianDistribution( float(i + 1), 0.0f, 3.0f ); /*我觉得这里应该是float(i+0)因为左边和右边等距点的权重一样*/
}
}
else {
for( int i = 1; i < 15; i += 2 ) {
vSampleOffsets[i + 0] = D3DXVECTOR2( 0.0f, i * vViewportTexelSize.y );
vSampleOffsets[i + 1] = D3DXVECTOR2( 0.0f, -i * vViewportTexelSize.y );
fSampleWeights[i + 0] = 2.0f * GetGaussianDistribution( 0.0f, float(i + 0), 3.0f );
fSampleWeights[i + 1] = 2.0f * GetGaussianDistribution( 0.0f, float(i + 1), 3.0f );
}
}
}
转载于:https://www.cnblogs.com/ttthink/articles/1577789.html
最后
以上就是美好蓝天最近收集整理的关于高斯分布函数解析的全部内容,更多相关高斯分布函数解析内容请搜索靠谱客的其他文章。
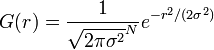
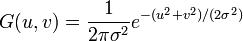








发表评论 取消回复