概述
1.线性可分支持向量机
首先来说，支持向量机其实就是样本与超平面之间的间隔最大，其实是一个求最优问题。在说间隔最大的问题前，先说函数间隔和几何间隔。
1.1 函数间隔与几何间隔
对于给定的训练数据集T和超平面（w,b），定义超平面（w，b）关于样本点（xi,yi）的函数间隔为
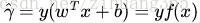
定义超平面（w,b）关于训练数据集T的函数间隔为超平面（w,b）关于T中所有样本点（xi,yi）的函数间隔最小值，为：
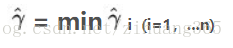
函数间隔表示分类预测的正确性及确信度，但只有函数间隔还不够，因为若w,b变成2w,2b，超平面并没有变化，但是函数间隔变为原来的2倍，所以需要对w加约束，规范化||w|| = 1，即函数间隔转换成几何间隔。
几何间隔为：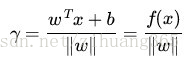 
一般当样本点（xi,yi）被超平面（w,b）正确分类时，点xi与超平面（w,b）的距离为：
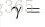yi （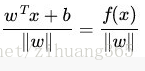
）
1.2间隔最大化
由上面发现几何间隔是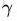
，求最大间隔分离超平面，表示为带有约束最优化问题：
max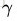 
s.t. yi （）>=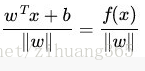
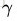
函数间隔与几何间隔仅差除个||w||，
2.拉格朗日乘子法以及KKT条件
拉格朗日乘子法是一种优化算法，主要用来解决约束优化问题。他的主要思想是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有n+k个变量的无约束优化问题。
利用拉格朗日乘子法主要解决的问题为：等式的约束条件和不等式的条件约束。
对于非等约束条件的求解，需要满足KKT条件才能进行求解。下面对于KKT条件进行分析。
不等式约束优化问题：
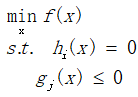
得到拉格朗日乘子法的求解方程：
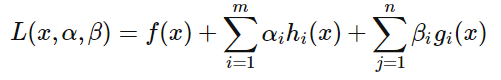
给出KKT条件：
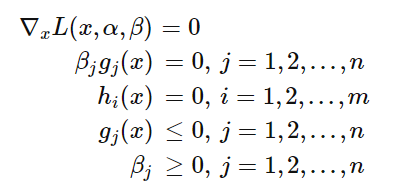
3.为什么给出KKT条件？
我们引入拉格朗日函数L(x,α,β)将有约束的优化问题转换为无约束的优化问题，然后对原问题的参数求导，获得使拉格朗日函数最小的拉格朗日对偶函数g(α,β)，最后使得对偶函数最大的问题则成为原问题的对偶问题。（对偶函数给出了主问题最优解的下界。那么下界最大是什么，这就是主问题的对偶问题）
因此对于上面拉格朗日乘子法问题的描述表达为：
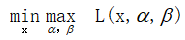
但其实是仍然个很难解决的问题，因为我们要先解决不等式约束的max问题，然后再在x上求最小值。怎么办呢？如果能把顺序换一下，先解决关于x的最小值，在解决关于α、β的不等式约束问题就好了。即，
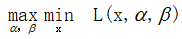
假设原问题为p，对偶问题为d，事实上，p和d并不完全相等，此处含有一个性质：弱对偶性
即：
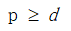
而他两个的差即为对偶间隙
解释：我们是想通过对偶问题求解原问题的最优解，所以只有当二者相等时才可能将原问题转化成对偶问题进行求解。消除对偶间隙，使p = d,需要满足一定条件，而这个条件便是 slater条件和KTT条件。
在凸优化理论中，有一个Slater定理，当这个定理满足，结合KKT条件，那么对偶间隙就会消失，就是强对偶性成立。
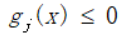
最后
以上就是幽默棉花糖为你收集整理的SVM（支持向量机）函数间隔与几何间隔仅差除个||w||， = 2.拉格朗日乘子法以及KKT条件3.为什么给出KKT条件？的全部内容，希望文章能够帮你解决SVM（支持向量机）函数间隔与几何间隔仅差除个||w||， = 2.拉格朗日乘子法以及KKT条件3.为什么给出KKT条件？所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
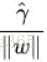
发表评论 取消回复