向量的内积外积与其几何意义

80 阅读 0 评论 53 点赞

我是靠谱客的博主健忘小白菜，最近开发中收集的这篇文章主要介绍向量的内积外积与其几何意义，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、点乘（内积）

有向量 $a=(x_1,y_1)，vec b=(x_2,y_2)$ ，夹角为 $θ$ ，内积为：
$b|costheta=x_1x_2 + y_1y_2$

几何意义：

夹角，由 $a \cdot b = ∣ a ∣ ∣ b ∣ cos θ$ 知，当内积 $> 0$ ， $theta<90^circ$ ，内积 $< 0$ ， $theta>90^circ$ ，内积 $= 0$ ， $theta=90^circ$ 。同时也可以计算 $θ$ 的值： $θ = a r c c o s a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ ∣ b ⃗ ∣ theta=arccosfrac {vec a cdot vec b}{|vec a||vec b|}$
投影， $∣ a ⃗ ∣ cos ⁡ θ = a ⃗ ⋅ b ⃗ ∣ b ⃗ ∣ |vec a|costheta=frac {vec a cdot vec b}{|vec b|}$ 表示 $a$ 在 $b$ 上的投影。
对偶性： $a \cdot b = ∣ a ∣ (∣ b ∣ cos θ) = ∣ b ∣ (∣ a ∣ cos θ)$
$∣ a ∣ (∣ b ∣ cos θ)$ 的理解是 $a$ 的长度与 $b$ 在 $a$ 上的投影的乘积；
$∣ b ∣ (∣ a ∣ cos θ)$ 的理解是 $b$ 的长度与 $a$ 在 $b$ 上的投影的乘积；
而这两个是相等的。

二、叉乘（外积）

在这里插入图片描述
上面的公式，就是求三阶行列式。

几何意义：

上面如果不把 $i, j, k$ 的具体指带入公式，而是写成 $a \times b = m i + n j + l k$ 的形式，向量 $(m, n, l)$ 就是一个同时垂直 $a$ 和 $b$ 的向量，如下图：
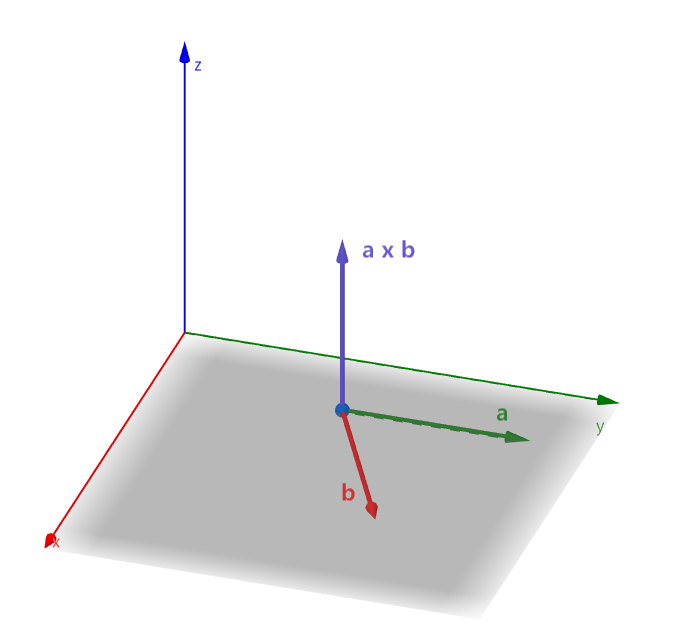
对于二维向量， $a=(x_1,y_1)，vec b=(x_2,y_2)$ ，按照上面的公式得：
$x_1 & y_1 \ x_2 & y_2 \ end{vmatrix}=x_1y_2-x_2y_1$ ，设这个数值为 $m$ 。
则， $∣ m ∣ = ∣ a \times b ∣ = ∣ a ∣ ∣ b ∣ sin θ$ （ $θ$ 为 $a$ 和 $b$ 的夹角）
且，|m| = $a$ 和 $b$ 构成的平行四边形的面积，如下图：
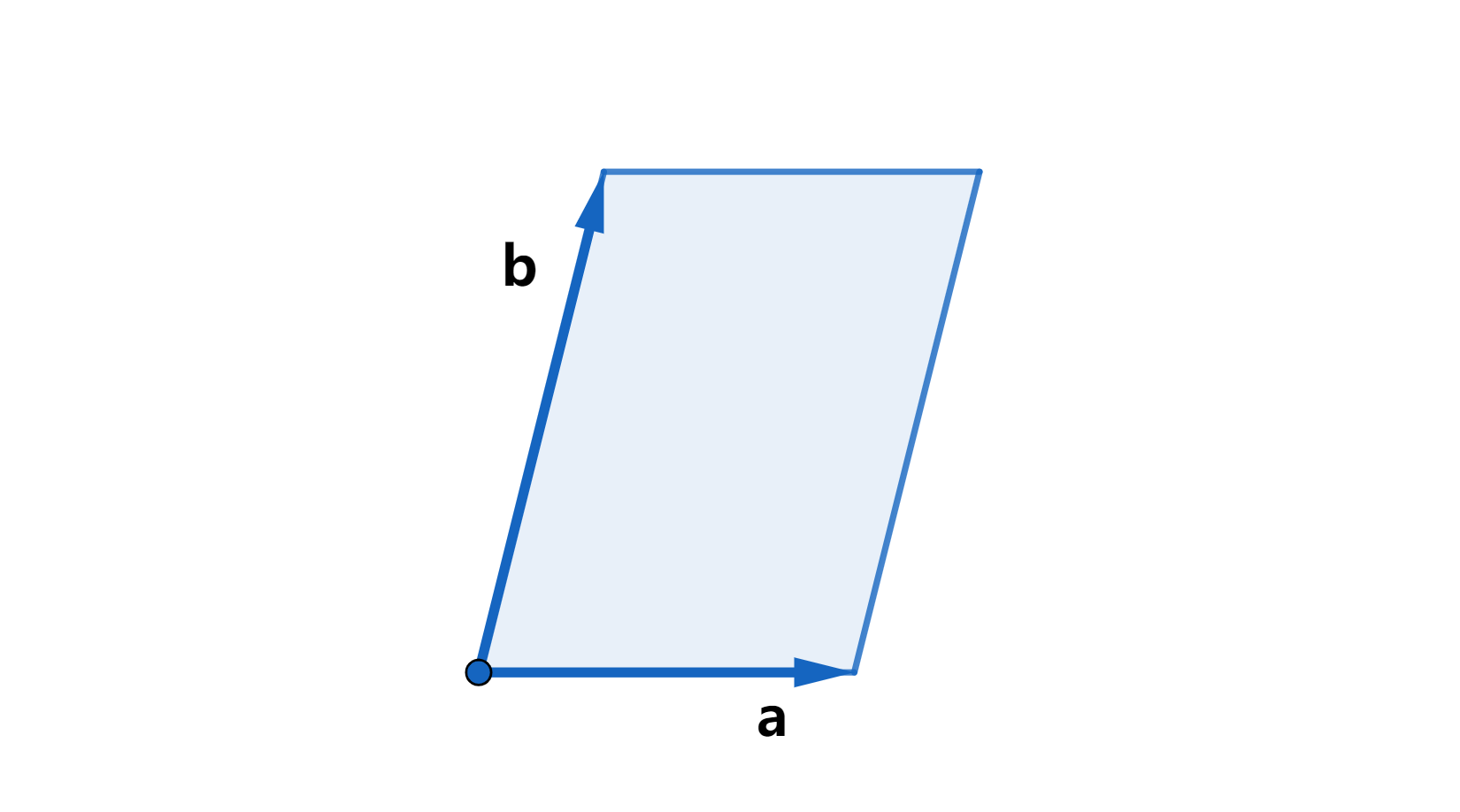
判断向量的相对位置（顺逆时针）
$a$ 和 $b$ 如图所示：

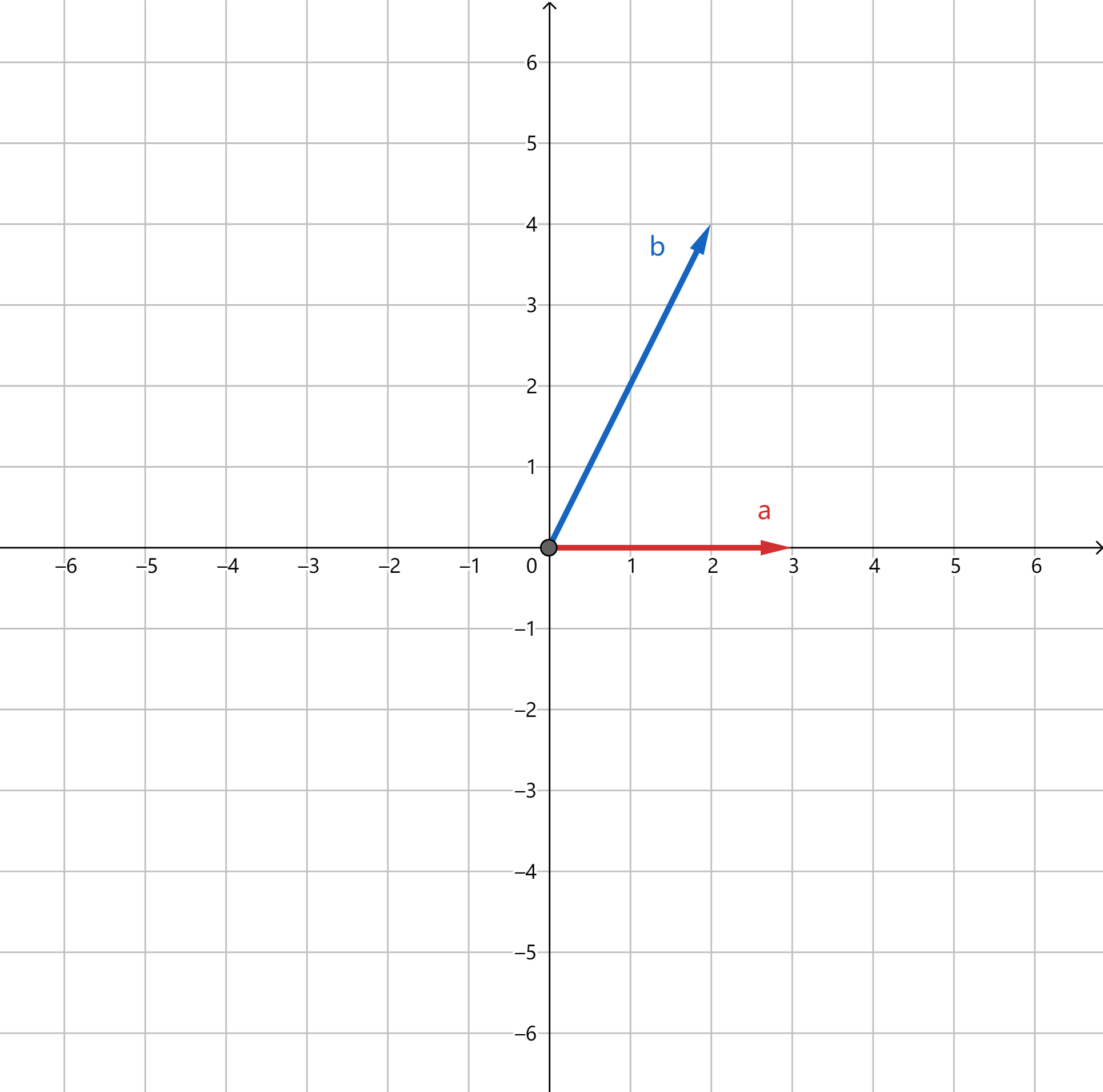
在这里插入图片描述
如果让 $a$ 以最小角度转到 $b$ 的方向，是顺时针还是逆时针呢，从图中很容易看出，但怎么用数字判断呢？
仍然是 $b=x_1y_2-x_2y_1$ ，
当 $m > 0$ ， $a$ 逆时针转到 $b$ 的角度 $<180^circ$ ，
当 $m < 0$ ， $a$ 逆时针转到 $b$ 的角度 $>180^circ$ ，
当 $m = 0$ ， $a$ 和 $b$ 共线。

直观记忆如下图：
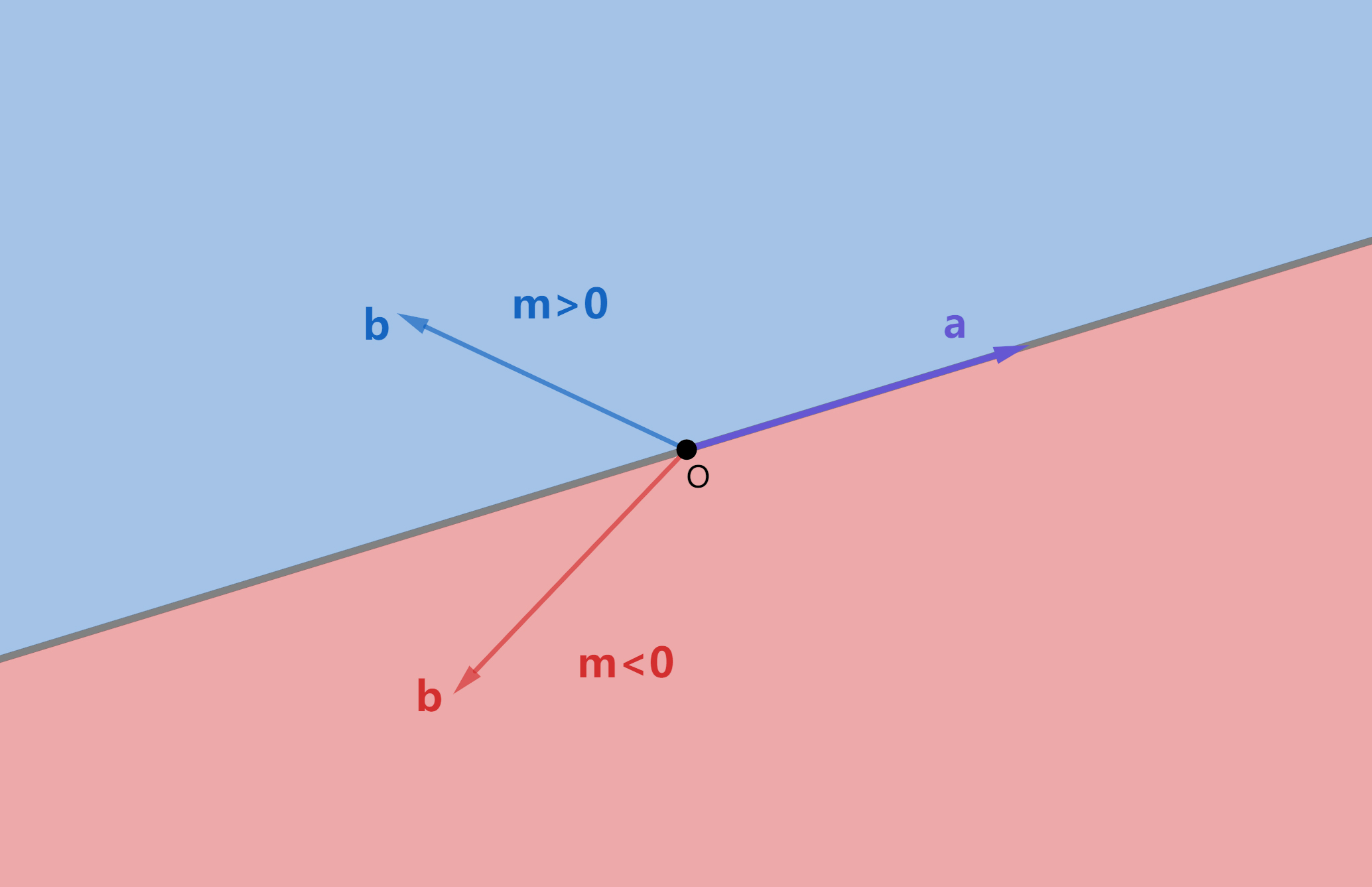
在这里插入图片描述
$m > 0$ ， $b$ 在蓝色部分；
$m < 0$ ， $b$ 在红色部分；
$m = 0$ ， $b$ 在分界线上（与 $a$ 共线）。

三、扩展（坐标系引发的顺逆指针分不清事件）

我们平时默认的坐标系是这样的：
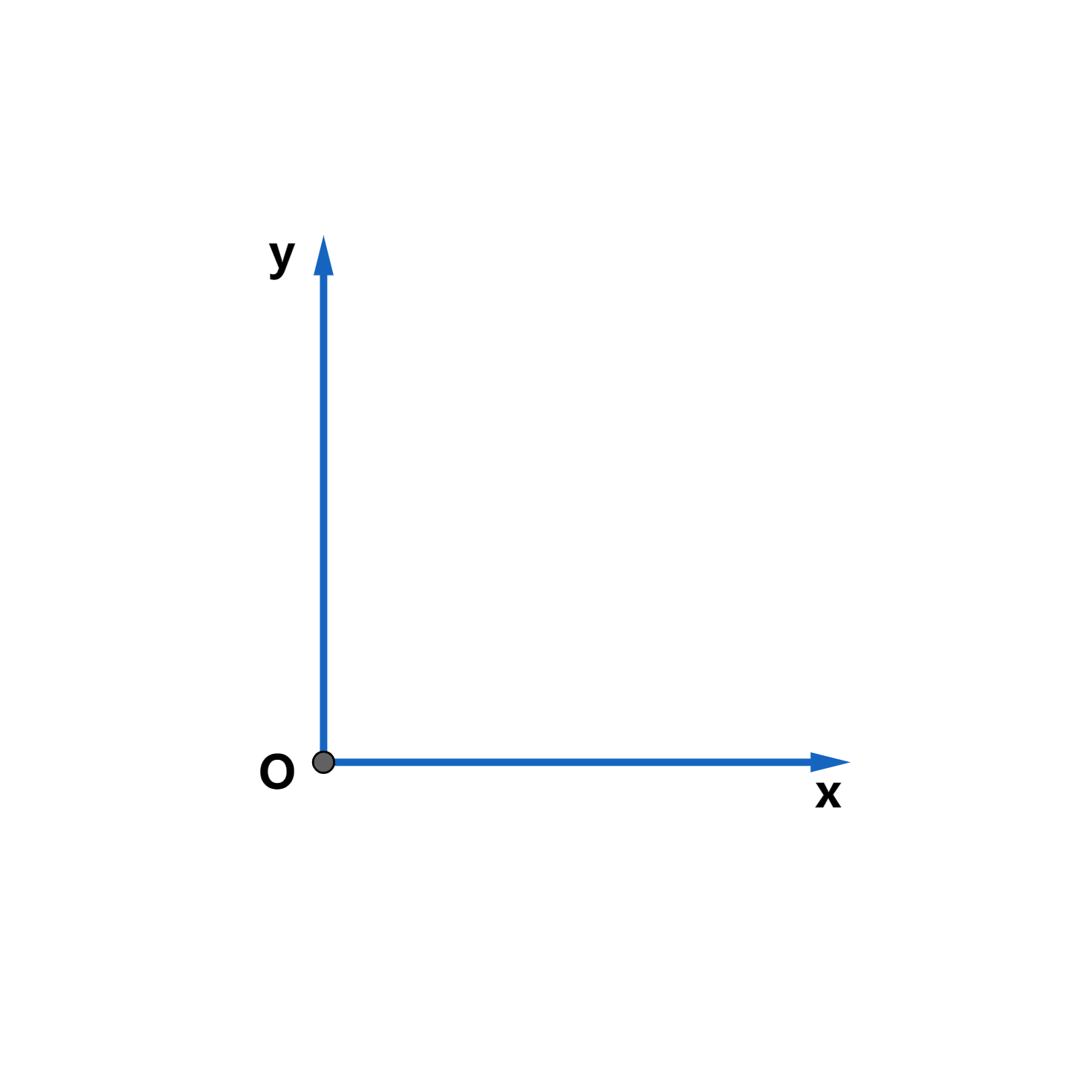
在这里插入图片描述
但有时候的坐标系是这样的（比如数字图像中）：

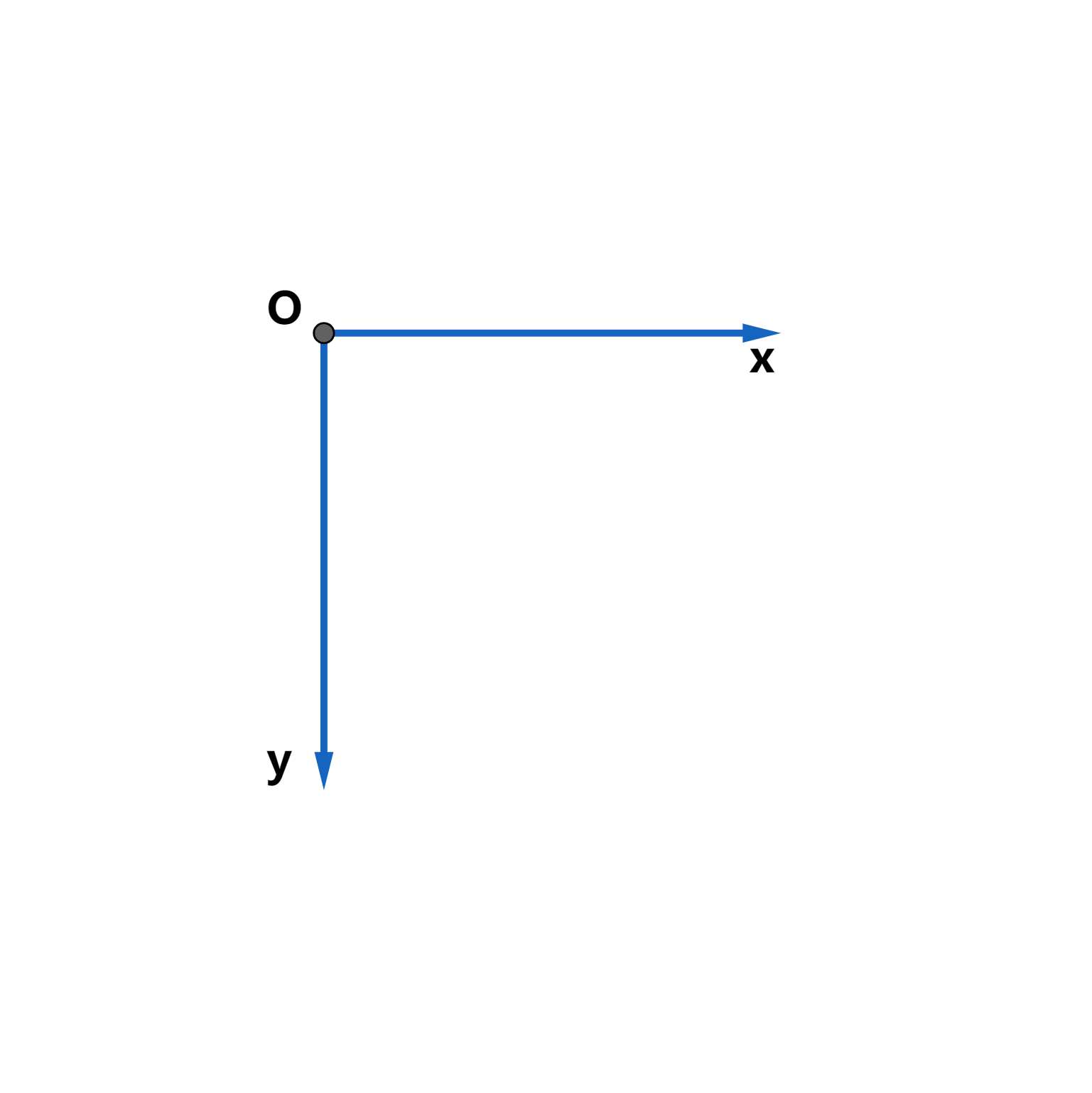
可以发现，同样的 $a = (2, 1)$ 转到 $b = (1, 2)$ ，在上面的坐标系中就是逆时针，而在下面的坐标系中就是顺时针，所以为了统一说明，定义了 “正旋转” ：从 $x$ 轴旋转到 $y$ 轴的方向。
所以，上面利用向量叉乘判断向量相对位置的性质描述应该为：
当 $m > 0$ ， $a$ 正旋转到 $b$ 的角度 $<180^circ$ ，
当 $m < 0$ ， $a$ 正旋转到 $b$ 的角度 $>180^circ$ ，
当 $m = 0$ ， $a$ 和 $b$ 共线。
而那张直观记忆图只在我们平时默认的坐标系中才成立。