单应性(Homography)变换
文章目录
- 单应性(Homography)变换
- 1. 概念
- 2. 在CV方面的应用
- 3. 求解单应性矩阵
- 3.1 假设
- 3.2 性质
- 3.3 求解
- 4. 优化
- 5. 推荐阅读
单应性变换的严格数学定义请参考:
- 《Multiple View Geometry in Computer Vision -2nd Edition》 by Richard Hartley, Andrew Zisserman
- 第2.3节Projective transformations
1. 概念
-
单应性变换又叫投影变换:应用在平面坐标变换中:
- 平面投影变换是在三元素向量的齐次坐标下进行的线性变换,他由一个3×3的非奇异变换矩阵 H H H表示,具体如下:
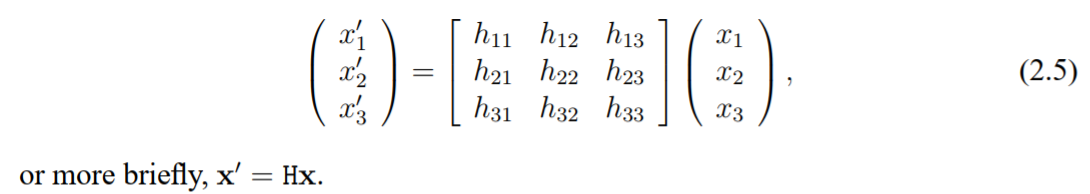
- x ′ x^{'} x′和 x x x都是齐次坐标,一般的有: x 3 ′ = x 3 = 1 x_{3}^{'}=x_{3}=1 x3′=x3=1
-
单应性矩阵:
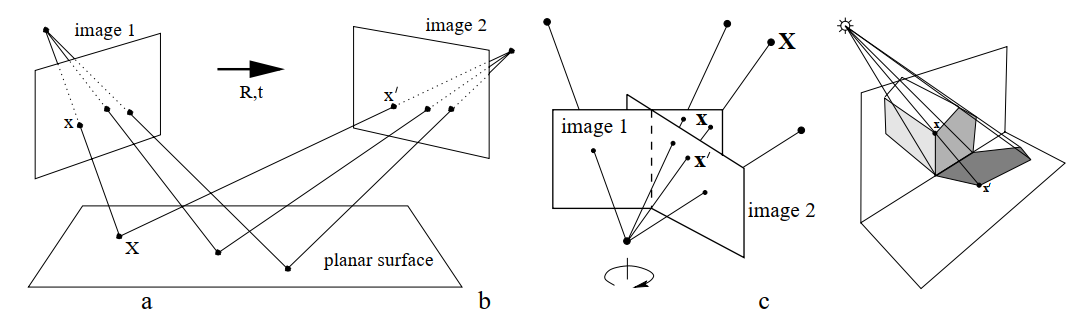
- 单应矩阵描述两个平面上的对应点之间的变换关系;
- 同一个平面在任意坐标系之间都可以建立单应性变换关系;
- 如(a):plannar surface上的X点可以通过单应性矩阵 H 1 H_{1} H1和 H 2 H_{2} H2变换到image1和image2,(b)和(c)同理。
2. 在CV方面的应用
-
图像校正、图像拼接、相机位姿估计、视觉SLAM等。
-
图像校正
-
视角变化
-
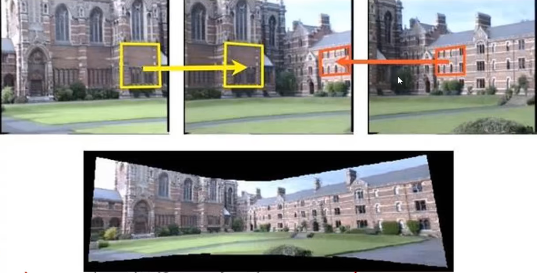
图像拼接
-
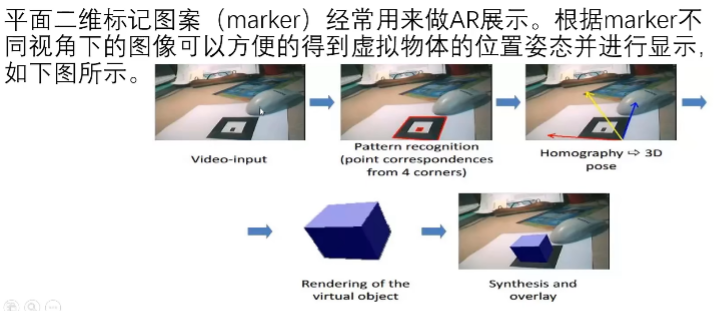
AR
3. 求解单应性矩阵
3.1 假设
- 首先,我们假设两张图像中的对应点对齐次坐标为
P
x
y
=
(
x
,
y
,
1
)
T
P_{xy}=(x,y,1)^{T}
Pxy=(x,y,1)T和
P
u
v
=
(
u
,
v
,
1
)
T
P_{uv}=(u,v,1)^{T}
Puv=(u,v,1)T,单应矩阵H定义为:
- H = [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] H=begin{bmatrix} h_{11} & h_{12} & h_{13} \ h_{21} & h_{22} & h_{23} \ h_{31} & h_{32} & h_{33} end{bmatrix} H=⎣⎡h11h21h31h12h22h32h13h23h33⎦⎤
- [ u v 1 ] = s [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] [ x y 1 ] ( 1 ) begin{bmatrix} u \ v \ 1 end{bmatrix} =s begin{bmatrix} h_{11} & h_{12} & h_{13} \ h_{21} & h_{22} & h_{23} \ h_{31} & h_{32} & h_{33} end{bmatrix}begin{bmatrix} x \ y \ 1 end{bmatrix}qquadqquadqquadqquadqquadqquad(1) ⎣⎡uv1⎦⎤=s⎣⎡h11h21h31h12h22h32h13h23h33⎦⎤⎣⎡xy1⎦⎤(1)
3.2 性质
- 这里使用的是齐次坐标系,也就是说可以进行任意尺度的缩放(s为尺度因子),也就是说把H乘以任意一个非零常数k并不改变上式结果,无非就是尺度因子s有所改变。
- 比如我们把H乘以
1
h
33
frac{1}{h_{33}}
h331可以得到:
- H ′ = 1 h 33 H = 1 h 33 [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] = [ h 11 ′ h 12 ′ h 13 ′ h 21 ′ h 22 ′ h 23 ′ h 31 ′ h 32 ′ 1 ] H'=frac{1}{h_{33}}H=frac{1}{h_{33}}begin{bmatrix} h_{11} & h_{12} & h_{13} \ h_{21} & h_{22} & h_{23} \ h_{31} & h_{32} & h_{33} end{bmatrix}=begin{bmatrix} h_{11}' & h_{12}' & h_{13}' \ h_{21}' & h_{22}' & h_{23}' \ h_{31}' & h_{32}' & 1 end{bmatrix} H′=h331H=h331⎣⎡h11h21h31h12h22h32h13h23h33⎦⎤=⎣⎡h11′h21′h31′h12′h22′h32′h13′h23′1⎦⎤
- 而上述等式依然成立
- 同理H乘以
1
∑
i
=
1
3
∑
j
=
1
3
h
i
j
2
frac{1}{sqrt{sum_{i=1}^3sum_{j=1}^3h_{ij}^{2}}}
∑i=13∑j=13hij21 可以得到约束:
- h 11 ′ 2 + h 12 ′ 2 + h 13 ′ 2 + h 21 ′ 2 + h 22 ′ 2 + h 23 ′ 2 + h 31 ′ 2 + h 32 ′ 2 + h 33 ′ 2 = 1 h_{11}'^{2} + h_{12}'^{2} + h_{13}'^{2} + h_{21}'^{2} + h_{22}'^{2} + h_{23}'^{2} + h_{31}'^{2} + h_{32}'^{2} + h_{33}'^{2}=1 h11′2+h12′2+h13′2+h21′2+h22′2+h23′2+h31′2+h32′2+h33′2=1
- 即 ∑ i = 1 3 ∑ j = 1 3 h i j ′ 2 = 1 sum_{i=1}^3sum_{j=1}^3h_{ij}'^{2}=1 ∑i=13∑j=13hij′2=1
- 由此我们可以得出单应性矩阵有8个自由度,并非9个自由度。
- 比如我们把H乘以
1
h
33
frac{1}{h_{33}}
h331可以得到:
3.3 求解
- 由3.1中假设公式(1)可得:
- { u = h 11 x + h 12 y + h 13 h 31 x + h 32 y + h 33 v = h 21 x + h 22 y + h 23 h 31 x + h 32 y + h 33 left{begin{array}{ll} u=frac{h_{11}x + h_{12}y + h_{13}}{h_{31}x + h_{32}y + h_{33}} \ v=frac{h_{21}x + h_{22}y + h_{23}}{h_{31}x + h_{32}y + h_{33}}end{array} right. {u=h31x+h32y+h33h11x+h12y+h13v=h31x+h32y+h33h21x+h22y+h23,进一步变换得:
- { u ( h 31 x + h 32 y + h 33 ) = h 11 x + h 12 y + h 13 v ( h 31 x + h 32 y + h 33 ) = h 21 x + h 22 y + h 23 left{begin{array}{ll} u(h_{31}x + h_{32}y + h_{33})=h_{11}x + h_{12}y + h_{13} \ v(h_{31}x + h_{32}y + h_{33})=h_{21}x + h_{22}y + h_{23}end{array} right. {u(h31x+h32y+h33)=h11x+h12y+h13v(h31x+h32y+h33)=h21x+h22y+h23,进一步得到:
- { x h 11 + y h 12 + h 13 − u x h 31 − u y h 32 − u h 33 = 0 x h 21 + y h 22 + h 23 − v x h 31 − v y h 32 − v h 33 = 0 left{begin{array}{ll} xh_{11} + yh_{12} + h_{13} - uxh_{31} - uyh_{32} - uh_{33}=0\ xh_{21} + yh_{22} + h_{23} - vxh_{31} - vyh_{32} - vh_{33}=0end{array} right. {xh11+yh12+h13−uxh31−uyh32−uh33=0xh21+yh22+h23−vxh31−vyh32−vh33=0,化成矩阵形式有:
- [ x y 1 0 0 0 − u x − u y − u 0 0 0 x y 1 − v x − v y − v . . . . . . . . . . . . . . . . . . . . . ] [ h 11 h 12 h 113 h 21 h 22 h 23 h 31 h 32 h 33 ] = 0 begin{bmatrix} x & y& 1& 0&0&0& - ux& -uy& -u \ 0&0&0&x & y& 1& - vx& -vy& -v \ ...\...\...\...\...\...\... end{bmatrix}begin{bmatrix} h_{11} \ h_{12} \ h_{113}\h_{21}\h_{22}\h_{23}\h_{31}\h_{32}\h_{33} end{bmatrix}=0 ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡x0.....................y0100x0y01−ux−vx−uy−vy−u−v⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡h11h12h113h21h22h23h31h32h33⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=0,更进一步抽象:
-
[
P
x
y
T
0
⃗
T
−
u
P
x
y
T
0
⃗
T
P
x
y
T
−
v
P
x
y
T
]
h
=
0
begin{bmatrix} P_{xy}^{T} & vec{0}^{T} & - uP_{xy}^{T} \ vec{0}^{T} &P_{xy}^{T} &- vP_{xy}^{T} end{bmatrix}h=0
[PxyT0T0TPxyT−uPxyT−vPxyT]h=0
- 其中 h = [ h 11 h 12 h 113 h 21 h 22 h 23 h 31 h 32 h 33 ] T h=begin{bmatrix} h_{11} & h_{12}& h_{113}&h_{21}&h_{22}&h_{23}&h_{31}&h_{32}&h_{33} end{bmatrix}^{T} h=[h11h12h113h21h22h23h31h32h33]T
- 0 ⃗ T = [ 0 0 0 ] vec{0}^{T}=begin{bmatrix} 0&0&0 end{bmatrix} 0T=[000]
- 我们发现一对点可以提供两个方程
- 由于单应矩阵H包含了 ∣ ∣ H ∣ ∣ F = ∑ i = 1 3 ∑ j = 1 3 h i j ′ 2 = 1 ||H||_{F}=sum_{i=1}^3sum_{j=1}^3h_{ij}'^{2}=1 ∣∣H∣∣F=∑i=13∑j=13hij′2=1或者 h 33 = 1 h_{33}=1 h33=1约束,因此根据上式的线性方程组8自由度的H我们至少需要4对点才能计算出单应矩阵。
4. 优化
但是,以上只是理论推导,在真实的应用场景中,我们计算的点对中都会包含噪声。比如点的位置偏差几个像素,甚至出现特征点对误匹配的现象,如果只使用4个点对来计算单应矩阵,那会出现很大的误差。因此,为了使得计算更精确,一般都会使用远大于4个点对来计算单应矩阵。另外上述方程组采用直接线性解法通常很难得到最优解,所以实际使用中一般会用其他优化方法如奇异值分解、Levenberg-Marquarat(LM)算法等进行求解,具体的优化过程可以参考张正友相机标定中得优化方法。
5. 推荐阅读
(超详细)张氏标定法原理及公式推导
最后
以上就是优美酸奶最近收集整理的关于单应性(Homography)变换与单应性矩阵的求解单应性(Homography)变换的全部内容,更多相关单应性(Homography)变换与单应性矩阵内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。











发表评论 取消回复