摄像机标定(Camera calibration)中存在的一个关键问题：如何求解投影矩阵有了投影矩阵，我们便可以把世界坐标系变化到图像坐标系。
一、最小二乘法
已知条件
n个三维世界坐标点(保存在dat文件中)
n个二维图像坐标点(保存在dat文件中)
使用工具：
环境：windows10+python3.7+pycharm2019
第三方库：numpy
代码如下：
1. 读取dat文件
其中文件每一行都是一个三维坐标或二维坐标，因此按行读取，按列存储
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21# 三维 x3, y3, z3 = [], [], [] with open("data_3.dat") as f: for line in f: tmp3 = line.split() if tmp3: # 防止文件空行 x3.append(float(tmp3[0])) y3.append(float(tmp3[1])) z3.append(float(tmp3[2])) # 二维 x2, y2 = [], [] with open("data_2.dat") as f: for line in f: tmp2 = ine.split() if tmp2: x2.append(float(tmp2[0])) y2.append(float(tmp2[1]))
2. 表示矩阵K(矩阵K见论文，大小为2n*11）
1
2
3
4
5
6
7
8
9
10
11# 表示矩阵K k = np.zeros((len(x3)*2, 11), dtype=int) for i in range(len(x3)): k[2 * i][0], k[2 * i][1], k[2 * i][2], k[2 * i][3] = x3[i], y3[i], z3[i], 1 k[2 * i][4], k[2 * i][5], k[2 * i][6], k[2 * i][7] = 0, 0, 0, 0 k[2 * i][8], k[2 * i][9], k[2 * i][10] = -x2[i]*x3[i], -x2[i]*y3[i], -x2[i]*z3[i] k[2 * i + 1][0], k[2 * i + 1][1], k[2 * i + 1][2], k[2 * i + 1][3] = 0, 0, 0, 0 k[2 * i + 1][4], k[2 * i + 1][5], k[2 * i + 1][6], k[2 * i + 1][7] = x3[i], y3[i], z3[i], 1 k[2 * i + 1][8], k[2 * i + 1][9], k[2 * i + 1][10] = -y2[i] * x3[i], -y2[i] * y3[i], -y2[i] * z3[i]
3. 表示矩阵U(矩阵U见论文，大小为11*1）
1
2
3
4
5U = np.zeros((len(x3)*2, 1), dtype=int) for i in range(len(x3)): U[2 * i] = x2[i] U[2 * i + 1] = y2[i]
4.根据最小二乘法可知投影矩阵m为：
1
2
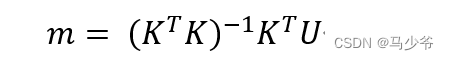
3# 计算投影矩阵 m = np.matmul(np.matmul(np.linalg.inv(np.matmul(k.T, k)), k.T), U)
由于此时得到的m为11维向量，而投影矩阵大小为(3,4).根据论文中指出m(3,4)=1
因此需将1添加到m中并变换矩阵m的尺寸为3*4
1
2
3
4
5
6
7
8list_m = [] for i in range(11): list_m.append(m[i][0]) list_m.append(1) m_matrix = np.array(list_m).reshape(3, 4)
5. 验证投影矩阵m是否正确
方法：将投影矩阵与某一个三维世界坐标进行矩阵乘法运算，看看结果是否得到对应的二维图像坐标，若是，则得到正确的投影矩阵m。
由于每个人的坐标数据不一样，因此这一步可自行编写相关代码进行验证。
二、特征向量法
1. 读取dat文件
其中文件每一行都是一个三维坐标或二维坐标，因此按行读取，按列存储
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21# 三维 x3, y3, z3 = [], [], [] with open("data_3.dat") as f: for line in f: tmp3 = line.split() if tmp3: # 防止文件空行 x3.append(float(tmp3[0])) y3.append(float(tmp3[1])) z3.append(float(tmp3[2])) # 二维 x2, y2 = [], [] with open("data_2.dat") as f: for line in f: tmp2 = ine.split() if tmp2: x2.append(float(tmp2[0])) y2.append(float(tmp2[1]))
2. 表示矩阵A(矩阵A见论文，大小为2n*12）
1
2
3
4
5
6
7
8
9
10
11# 表示矩阵A(下面的k即为矩阵A) k = np.zeros((len(x3)*2, 12), dtype=int) for i in range(len(x3)): k[2 * i][0], k[2 * i][1], k[2 * i][2], k[2 * i][3] = x3[i], y3[i], z3[i], 1 k[2 * i][4], k[2 * i][5], k[2 * i][6], k[2 * i][7] = 0, 0, 0, 0 k[2 * i][8], k[2 * i][9], k[2 * i][10], k[2 * i][11] = -x2[i]*x3[i], -x2[i]*y3[i], -x2[i]*z3[i], -x2[i] k[2 * i + 1][0], k[2 * i + 1][1], k[2 * i + 1][2], k[2 * i + 1][3] = 0, 0, 0, 0 k[2 * i + 1][4], k[2 * i + 1][5], k[2 * i + 1][6], k[2 * i + 1][7] = x3[i], y3[i], z3[i], 1 k[2 * i + 1][8], k[2 * i + 1][9], k[2 * i + 1][10], k[2 * i + 1][11] = -y2[i] * x3[i], -y2[i] * y3[i], -y2[i] * z3[i], -y2[i]
3.计算ATA的特征值与特征向量：
1
2
3# 计算ATA的特征值与特征向量 eigenvalue, featurevector = np.linalg.eig(np.matmul(k.T, k))
4.获得最小特征值的索引：
1
2index = np.argmin(eigenvalue)
6. m(3, 4)元素归一化
由于此时得到的特征向量中的m(3, 4)并不为1，参考另一篇博文得知m(3, 4)元素值为1，因此，将m(3, 4)元素归一化(对投影矩阵操作)
1
2m_matrix = m_matrix / m_matrix[-1, -1]
7. 验证投影矩阵m是否正确
方法：将投影矩阵与某一个三维世界坐标进行矩阵乘法运算，看看结果是否得到对应的二维图像坐标，若是，则得到正确的投影矩阵m。
由于每个人的坐标数据不一样，因此这一步可自行编写相关代码进行验证。
最后
以上就是执着荷花最近收集整理的关于相机投影矩阵的计算的全部内容，更多相关相机投影矩阵内容请搜索靠谱客的其他文章。
发表评论 取消回复