问题描述

在计算机中，常用像素点的灰度值序列{p1,p1,……pn}表示图像。其中整数pi,1<=i<=n，表示像素点i的灰度值。通常灰度值的范围是0-255。因此需要8位二进制数来表示一个像素。这个时候大家应该有了一些小的疑问：我能不能用更少的位数来表示灰度值？（因为有的灰度值并没有达到255这么大）所以我们引入了图像压缩算法来解决这个问题。
不过在引入问题之前，我要在这里介绍一些算法设计的知识——我们要将灰度值序列分组，而每一组中所有的数就有可能是<255的，所以我们就不需要用8位数字去表示像素大小了，但是分组会带来一个新的问题：我如何表示当前组中像素的个数和像素的位数呢（因为不是八位，所以要有一个数据来记录真正的位数）？这里我们引入两个固定位数的值来表示，①我们用3位数字来表示当前组的每一位像素的的位数②我们引入8来表示当前组中像素点的个数　　因为我们在这里规定了一组中最多存储–>0~255个数字，而一个灰度值最多有8位（2^3），所以我们可以用即3位数字来表示当前组的像素位数（注意这里都是二进制）
压缩的原理就是把序列{p1,p1,……pn}进行设断点，将其分割成一段一段的。分段的过程就是要找出断点，让一段里面的像素的最大灰度值比较小，那么这一段像素(本来需要8位)就可以用较少的位(比如7位)来表示，从而减少存储空间。
b代表bits,l代表length,分段是，b[i]表示每段一个像素点需要的最少存储空间(少于8位才有意义)，l[i]表示每段里面有多少个像素点，s[i]表示从0到i压缩为一共占多少存储空间。
如果限制l[i]<=255,则需要8位来表示l[i]。而b[i]<=8，需要3位表示b[i]。所以每段所需的存储空间为l[i]*b[i]+11位。假设将原图像分成m段，那么需要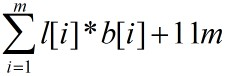位的存储空间。
图像压缩问题就是要确定像素序列{p1,p1,……pn}的最优分段，使得依此分段所需的存储空间最小。

最优子结构

设l[i],b[i],1<=i<=m是{p1,p1,……pn}的一个最优分段，则l[1],b[1]是{p1,……,pl[1]}的一个最优分段，且l[i],b[i],2<=i<=m是{pl[1]+1,……,pn}的一个最优分段。即图像压缩问题满足最优子结构性质。

递推关系

设s[i],1<=i<=n是像素序列{p1,p1,……pi}的最优分段所需的存储位数，则s[i]为前i-k个的存储位数加上后k个的存储空间。由最优子结构性质可得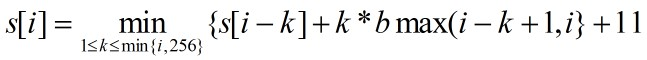：式中

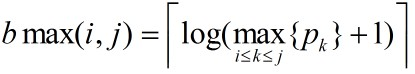
构造最优解

数组l[i],b[i]记录了最优分段所需的信息最优分段的最后一段的段长度和像素位数分别存储在l[n]和b[n]中,其前一段的段长度和像素位数存储于l[n-l[n]]和b[n-l[n]]中，依此类推，可在O(n)时间内构造最优解。

算法设计

{6, 5, 7,5, 245, 180, 28,28,19, 22, 25,20}这是一组灰度值序列。我们按照默认的解体方法来看----一共12个数字，所以12*8=96位来表示。
而下面我们将其进行分组：
这里我们将他们分为三组：

1. 第一组4个数，最大是7所以用3位表示；
2. 第二组2个数，最大是245所以用8位表示；
3. 第三组6个数，最大是28所以用5位表示；
4. 这个时候，我们最后得到了最后的位数结果为：43+28+65+113=91。是不是优化了？？
   那我们算法应该怎么做来找最优的值呢？？
   下面我一步一步介绍。
   压缩过程中的数组存储：
   既然是DP问题，所以我们肯定需要数组来记录每一步的最优值。这里我们用
   S[i]来记录前i个数字的最优处理方式得到的最优解。
   l[i]中来记录第当前第i个数所在组中有多少个数。(因而只有每一组的最后一个l[x],存储有效)（这句话，暂时看不懂也没关系）
   b[i]中存第i个数的像素位数。

下面我写出来具体的递推过程–>
例题:　求像素序列4，6，5，7，129，138，1的最优分段。

在解体过程中，我们知道在我们求s[3]的时候，我们是分三种情况----

1. 前三个数为一组，这个时候我需要的存储位数是3(位数)*3（每一组中数的个数）+11（每分一组所必须的固定位数）
2. s[1]为单独一组，剩下的两个数字为一组，此时我所需要的空间为s[1]+2*3+11
3. 前两个数字为一组，最后一个数为一组。此时我们要用s[2]（前面已经计算出的最优值）+3*1+11
   然后比较三个数的大小，取最小的那一种分组情况，然后记下l[3]=3（当前最优分组中是三个数在同一组中），b[3]=3（每一个像素所用的存储位数）
   递归到最后得到最优解为　　58.

伪代码

Algorithm 图像压缩
Input:
    Array,n //数组和数组大小
output:
    s[n]  //最小存储空间

function Compress(n,p[],s[],l[],b[])
    Lmax <- 256
    header <- 11
    s[0] <- 0
    for j = 2 -> n do
        b[i] <- length(p[i])    //计算像素点p需要的存储位数  
        bmax <- b[i]
        s[i] <- s[i-1] + bmax + header
        l[i] <- 1
        for j = 2 -> min(i,Lmax) do
        if bmax < length(p[i-j+1]) then
            bmax <- length(p[i-j+1])
        end if
        if s[i] > s[i-j+1] j*bmax + header then
            s[i] <- s[i-j] + j*bmax + header
            l[i] <- j
            b[i] <- bmax
        end if
    end for
end function

压缩部分代码

void Compress(int n,int p[],int s[],int l[],int b[])
{
    int Lmax = 256,header = 11;
    s[0] = 0;
    for(int i=1; i<=n; i++)
    {
        b[i] = length(p[i]);//计算像素点p需要的存储位数  
        int bmax = b[i];
        s[i] = s[i-1] + bmax + header;
        l[i] = 1;
        for(int j=2; j<=i && j<=Lmax;j++)  //最后一段含有一个像素，两个像素，所有像素
        {  
            //if(bmax<b[i-j+1])   //最后一个b[i-j+1]有效，是前一段当中的最大值，并不是后一段中的最大值
            if(bmax<length(p[i-j+1])) 
            {  
                bmax = length(p[i-j+1]);  
            }  
  
            if(s[i]>s[i-j]+j*bmax+header)  
            {  
                s[i] = s[i-j] + j*bmax+header;  
                l[i] = j;  
                b[i] = bmax;  //我加，跟新当前组，所需的存储位数
            }  
        }  
    }  
}  

完整代码

//代码参考：https://www.cnblogs.com/caiyishuai/p/8876077.html 
//dacao 2019/6/25
#include<iostream> 
#include<cmath>  
#include<stack>
using namespace std;   
  
const int N = 7;  
  
int length(int i);  
void Compress(int n,int p[],int s[],int l[],int b[]);  
int TraceBack(int n,int l[],int b[]);  //返回有多少个段
void Out(int m,int min_len,int l[],int b[]);
  
int main()  
{  
    //int p[] = {0,10,12,15,255,1,2};//图像灰度数组 下标从1开始计数  
      int p[] = {0,255,1,5,2,1,2};
    int s[N]={0},l[N]={0},b[N]={0};  
  
    cout<<"图像的灰度序列为："<<endl;  
  
    for(int i=1;i<N;i++)  
    {  
        cout<<p[i]<<" ";  
    }  
    cout<<endl;  
  
    Compress(N-1,p,s,l,b);  
    int m=TraceBack(N-1,l,b); 
    Out(m,s[N-1],l,b);
    return 0;  
}  
  
void Compress(int n,int p[],int s[],int l[],int b[])  
{  
    int Lmax = 256,header = 11;  
    s[0] = 0;  
    for(int i=1; i<=n; i++)  
    {  
        b[i] = length(p[i]);//计算像素点p需要的存储位数  
        int bmax = b[i];  
        s[i] = s[i-1] + bmax + header;  
        l[i] = 1;  
  
        for(int j=2; j<=i && j<=Lmax;j++)  //最后一段含有一个像素，两个像素，所有像素
        {  
            //if(bmax<b[i-j+1])   //最后一个b[i-j+1]有效，是前一段当中的最大值，并不是后一段中的最大值
            if(bmax<length(p[i-j+1])) 
            {  
                bmax = length(p[i-j+1]);  
            }  
  
            if(s[i]>s[i-j]+j*bmax+header)  
            {  
                s[i] = s[i-j] + j*bmax+header;  
                l[i] = j;  
                b[i] = bmax;  //我加，跟新当前组，所需的存储位数
            }  
        }  
    }  
}  
  
int length(int i)  
{   
    int k=1;  
    i = i/2;  
    while(i>0)  
    {  
        k++;  
        i=i/2;  
    }  
    return k;
   //return ceil(log(i+1)/log(2));  
}  

int TraceBack(int n,int l[],int b[]) //从后向前检查，因而之后对应段的，最后一个存储有效
{
    stack<int>ss;
    ss.push(l[n]);
    ss.push(b[n]);
    while (n!=0)
    {
        n=n-l[n];
        ss.push(l[n]);  //l[0]=0,也被压入栈中
        ss.push(b[n]);
    }
    int i=0;
    while (!ss.empty())
    {
        b[i]=ss.top();
        ss.pop(); 
        l[i]=ss.top(); //此时　ｌ[]，用来存储，第ｉ组中，元素个数
        ss.pop();
        i++;
    }
    return i-1;
}

void Out(int m,int min_len,int l[],int b[])
{
    int i=0;
    cout<<"最小长度："<<min_len<<endl;
    cout<<"共分成："<<m<<"段"<<endl;
    for(i=i+1;i<=m;i++)
    {
        cout<<"第一个段含有"<<l[i]<<"元素.   "<<"需要存储位数"<<b[i]<<endl;
    }
}

参考文章

0016算法笔记——【动态规划】图像压缩问题
图像压缩－－－动态规划
动态规划之–图像压缩

最后

以上就是忧伤橘子为你收集整理的算法笔记（0001） - 【动态规划】图像压缩问题问题描述最优子结构递推关系构造最优解算法设计伪代码完整代码参考文章的全部内容，希望文章能够帮你解决算法笔记（0001） - 【动态规划】图像压缩问题问题描述最优子结构递推关系构造最优解算法设计伪代码完整代码参考文章所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。