问题描述

数字化图像是n×n的像素阵列，假定每个像素有一个0～255的灰度值，即存储一个像素需8位。为了减少存储空间，采用变长模式，即不同的像素用不同位数来存储。最终使用较少的位数对所有像素点进行存储，从而节约存储空间。
为了简化问题，进行以下几步操作。
1）图像线性化：将n×n维图像转换为1×n²向量。{P1，P2，···Pn²}
2）分段：将像素分为连续m段s1，s2，···sm，使每段中像素存储位数相同，每段最多包含256个像素点。
3）创建三个表
L：l[i]存放第i段长度。（L:length）
B：b[i]存放第i段中像素的位数。（B:bits）
P：{P1，P2，···Pn²}以变长格式存储二进制串。
简单概括就是：将图像上平面分布的像素点线性排序，并将二进制位数相同的划分到同一集合（如5、6、7二进制表示分别为101、110、111，均为三位，则为同一划分)。找到划分的最佳断点，使得所需位数最小。创建三个表分别存储每个集合像素点个数、二进制位数、具体划分情况。

有一点需要特别注意，也是很让人迷惑的一点：在具体的计算中，每进行一次划分，就要加上11。l[i]表示每段里面有多少个像素点，最多为255个即8位二进制；b[i]表示每段一个像素点需要的存储空间，最多为8位即3位二进制。则为了存储每一个分段，需要(8+3)=11的代价

则将像素点分段后的像素像素压缩公式为

即每个划分中像素点个数与二进制位数的乘积加上11*划分数。
在此基础上，如何找到一个最优分段，使得存储空间最少。

递归策略

设l[i]，b[i]（i从1到m）是{P1，P2，···Pn²}的一个最优分段。则
l[1]，b[1]是{P1，P2，···Pn²}的一个最优分段。
l[i]，b[i]（i从2到m）是{P1，P2，···Pn²}的一个最优分段。
则此问题转化为递归问题，即向下不断寻找像素序列的最优分段。

算法设计

（1）考察最后一个元素p[i]的分段情况；
（2）假设p[i]自成一段，则s[i]=s[i-1]+保存最后一个像素点的代价；
（3）假设最后两个像素点为一段，则s[i]=s[i-2]+保存最后两个像素点的代价；
（4）假设最后i个像素点为一段，则s[i]=s[0]+保存最后i个像素点的代价；
如何确定最后多少个元素为一段？
（5）取令s[i]最小时对应的元素个数，假设为k；
（6）则s[i]=s[i-k]+保存最后k个像素的代价；
（7）最后k个像素的代价=k*max（这k个像素对应二进制数）+11
（8）求解则s[i-k]；
（9）重复以上步骤；

解题步骤

设s[i]（1≤i≤n）是像素序列{P1，P2，···Pn²}的最优分段所需存储位数。
i=1 p1

i=2 p1 p2

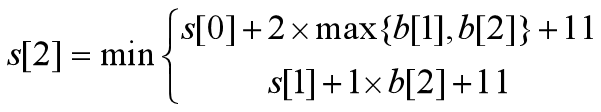
i=3 p1 p2 p3

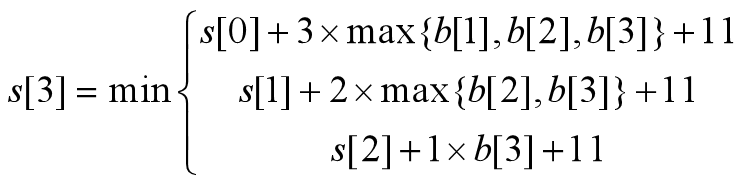
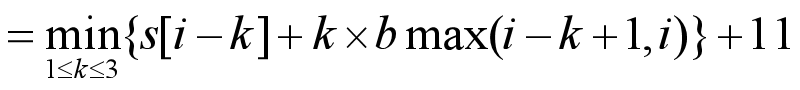则

例题

求像素序列4，6，5，7，129，138，1的最优分段。
解：

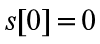
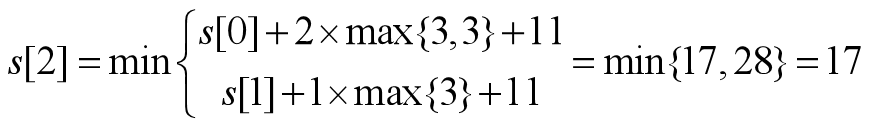
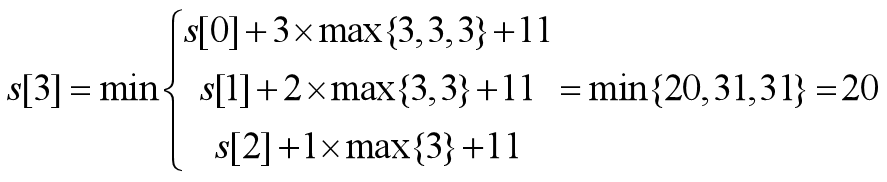
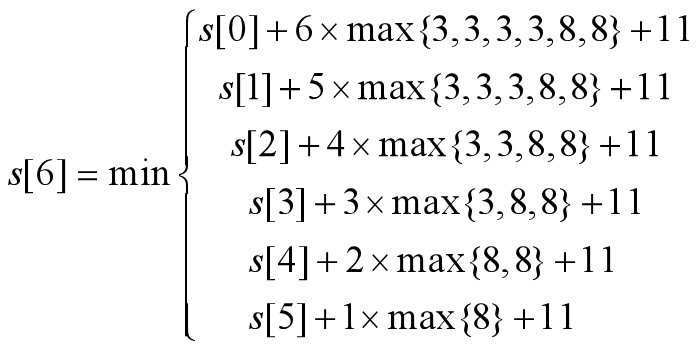
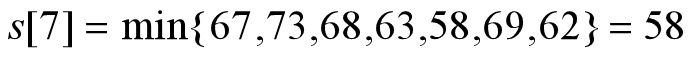
最后

以上就是自由马里奥为你收集整理的【动态规划】图像压缩问题问题描述递归策略算法设计解题步骤例题的全部内容，希望文章能够帮你解决【动态规划】图像压缩问题问题描述递归策略算法设计解题步骤例题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。